DIY laserstyringsmodul for Arduino: 14 trinn (med bilder)

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-30 11:24

I denne instruksen vil jeg demonstrere konstruksjonen av en dobbeltakset, enkelt-speil laserstråle styremodul ved hjelp av 3D-trykte deler og rimelige komponenter fra eBay.

Dette prosjektet har likhetstrekk med Arduino Laser Show med Full XY Control og Arduino Laser Show With Real Galvos, men jeg tror det er det første som bruker et 3D -trykt design med rimelige solenoider. Jeg legger alle designfilene under GPLv3 slik at designet kan forbedres og forbedres.

Selv om jeg for øyeblikket bare har satt sammen modulen og skrevet noen veldig grunnleggende testkoder, er håpet at jeg en dag kan ta den til neste nivå ved å innlemme vektorgrafikkoden fra mine tidligere instruerbare, super raske analoge spenninger fra Arduino.

Trinn 1: Samle delene som ikke er 3D-trykte

Laserenheten består av følgende deler:

• 4 mikro solenoider
• Ett 1/2 tommer speil
• Fire M3 skruer

De spesifikke solenoider jeg brukte ble kjøpt på eBay for $ 1,45 hver. Det runde speilet ble funnet i håndverksgangen på HobbyLobby - en pakke med 25 kostet meg mindre enn $ 3 dollar. Du kan også finne speil på eBay.

Du trenger også en billig laserpeker, igjen, fra eBay. En fiolett laser sammen med et skinnende vinylark er en utmerket kombinasjon for dette prosjektet!

Et sett med hjelpende hender er ikke nødvendig, men vil være svært nyttig for å holde og plassere laserpekeren. Et stort bindemiddelklips kan brukes til å holde strømknappen nede.

Du trenger en Arduino (jeg brukte en Arduino Nano) og en måte å kjøre solenoider på. Som VajkF har uttalt i kommentarene, kan du bruke ferdiglagde H-bro slik som de som er basert på L298 eller L9110. Disse er lett tilgjengelige på eBay for noen få dollar og kan også brukes til å kjøre motorer og robotprosjekter.

Siden jeg ikke hadde en H-bro, bygde jeg min egen driver av diskrete komponenter:

• Fire bipolare NPN -transistorer (jeg brukte en MPS3704)
• Fire motstander (jeg brukte 1,2k ohm motstand)
• Fire dioder (jeg brukte en 1N4004)
• Et 9V batteri og batterikontakt

De elektroniske komponentene var fra laboratoriet mitt, så jeg har ikke en eksakt kostnad for dem, men med mindre du allerede har delene eller kan fjerne dem, er det sannsynligvis mer kostnadseffektivt å bruke en forhåndsbygd H-bro. Likevel vil jeg gi skjemaene for å bygge din egen.

Trinn 2: 3D -utskrift av speilstyringsmodulen

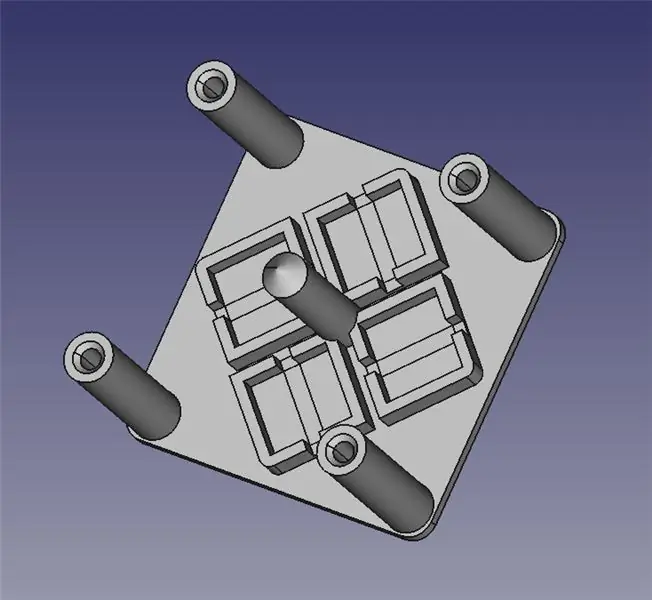
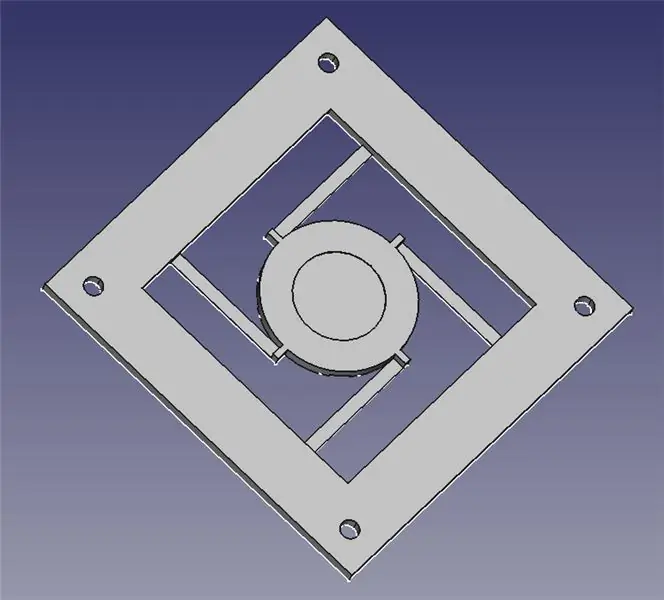
Laserstyringsmodulen består av to 3D -trykte deler: en base for montering av fire solenoider og en leddplattform for speilet.

Jeg har lagt ved de to STL -filene for deg til 3D -utskrift, samt FreeCAD -filer i tilfelle du trenger å endre designet. Alt innhold er under GPLv3, så du står fritt til å gjøre og dele forbedringene dine!

Trinn 3: Monter lasermodulen

• Bruk varmt lim for å feste de fire magnetventilene på det nedre stykket.
• Bruk varmt lim for å feste speilet på midten av det øvre stykket.
• Sett metallstemplene inn i magnetventilene og plasser det øvre stykket på stolpene (men ikke skru det ned). Roter toppstykket litt, og løft hvert stempel med en liten skrutrekker. Platen på skiven skal gli inn i sporet på stempelet. Vær forsiktig, ettersom 3D -trykte hengsler er veldig skjøre. Med tålmodighet og muligens noen få mislykkede forsøk, bør du kunne plassere alle fire stemplene uten å vri eller legge press på hengslene.
• Når alle stemplene er plassert, setter du inn M3 -skruene delvis, men før du strammer dem, skyver du forsiktig ned hvert stempel og sørger for at speilet vipper fritt. Hvis den ikke beveger seg fritt eller fanger seg, kan det være nødvendig å fjerne topplaten, lirke en eller flere solenoider løs og feste den igjen med en liten utadgående vinkel (avstandsstykker mellom den og den sentrale stolpen kan hjelpe med dette).

Trinn 4: Skriv ut laserpekerkragen

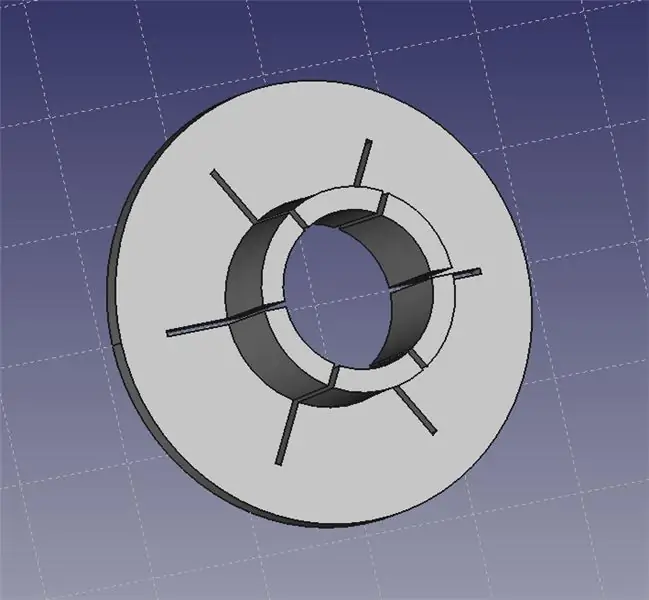
Laserpekerkragen passer på hodet på laserpekeren. Du kan deretter bruke et sett med hjelpende hender til å gripe kragen og la deg plassere laseren nøyaktig på benken din.

Trinn 5: Monter drivkretsen

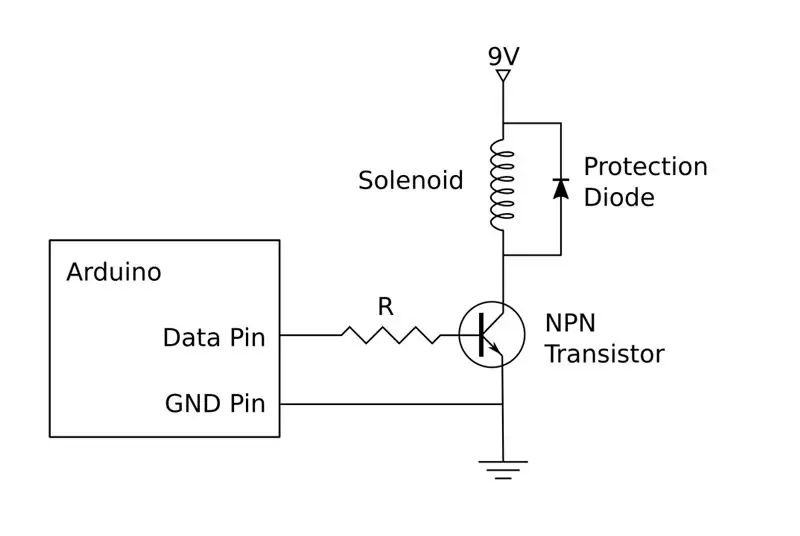
Drivkretsen er vist i diagrammet. Som nevnt tidligere, er min versjon bygget opp av diskrete komponenter, men du kan også bruke en lett tilgjengelig H-bro. Hvis du velger å bygge din egen, må du bygge fire kopier av denne kretsen, en for hver av de fire solenoider.

Hver krets vil koble til en Arduino -pinne, to for styring av venstre og høyre solenoid, og to for opp og ned solenoider. Disse må kobles til PWM -kompatible pinner, slik:

• Pin 9: Up Solenoid
• Pin 3: Down Solenoid
• Pin 11: Venstre magnetventil
• Pin 10: Høyre magnetventil

Et enkelt 9V -batteri kan brukes til å drive alle fire magnetventildriverkretsene, eller du kan bruke en strømforsyning ved bordet. Arduino -enheten går fra USB -strøm og bør ikke kobles til den positive siden av 9V -batteriet. Den negative siden av batteriet brukes imidlertid som bakkereferanse og bør kobles til GND-pinnen på Arduino så vel som til emitterpinnene på transistorene.

Trinn 6: Last opp prøvekoden

Eksempelkoden er oppdatert med følgende funksjoner:

• Justerer PWM -frekvensen slik at mekanismen er nesten stille ved lave hastigheter. Det summende i Motion Test 1 er helt borte!
• Legger til som spenningsligninger basert på papiret av Schimpf for å "linearisere" den ikke-lineære responsen til solenoider.

Jeg har også inkludert en implementering av en Lorenz Attractor basert på koden fra denne bloggen.

Troskapen til resultatene overlater ganske mye å være ønsket, men jeg jobber fortsatt med det!:)

De påfølgende trinnene illustrerer noen av teknikkene som brukes i koden.

Trinn 7: Skru ned volumet

I min bevegelsestest 1 kan du høre et høyt summende, spesielt under opp og ned bevegelse. Det viser seg at dette var forårsaket av at standard PWM -hakefrekvens for Arduino var innenfor det hørbare området. Den raske koblingen av spolen til og fra ville få dem til å vibrere ved den frekvensen, og gjøre dem til små små høyttalere.

For å løse dette problemet økte jeg PWM -frekvensen i koden:

#define PWM_FREQ_31372Hz 0x01 // Setter PWM -frekvensen til 31372,55 Hz #definerer PWM_FREQ_3921Hz 0x02 // Setter PWM -frekvensen til 3921,16 Hz #define PWM_FREQ_980Hz 0x03 // Setter PWM_TQ1TB1TQ1TF1TF1TQ1TF1TF1TF1TF1TF1TF1TF1TF1TFQTTV & 0b11111000) | Frekvens; // Still inn timer1 (pinner 9 og 10) frekvens TCCR2B = (TCCR2B & 0b11111000) | Frekvens; // Still inn timer2 (pinne 3 og 11) frekvens}

Innstilling av Arduino PWM -frekvensen er et nyttig triks for å stille ned solenoider eller motorer. Eksperimenter med de forskjellige valgene av frekvenser for å se hvilken som gir deg de beste resultatene. Selv om det innebærer litt mer avansert programmering, er en god ressurs for hvordan timerne fungerer her.

Trinn 8: Still inn spenningene for å redusere forvrengning

Mine første bevegelsestester viste at det var betydelig forvrengning i responsen til solenoider. I Motion Test 3 (venstre figur) ble det som skulle være en sirkulær spiral i stedet en rektangulær bane med ujevne kanter.

Å løse dette problemet krevde litt matematikk, men jeg klarte å finne et fantastisk papir på nettet som hjalp meg med å forstå problemet godt nok til å løse det i programvare.

Det som følger følger deg gjennom prosessen jeg gikk gjennom for å justere systemet og forbedre utseendet på de resulterende sporene!

Trinn 9: Perfeksjon av programvaren, med matematikk

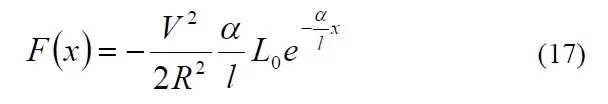
Hemmeligheten bak justeringen av systemet viste seg å være et utmerket papir kalt "A Detailed Explanation of Solenoid Force" av Paul H. Schimpf ved Eastern Washington University (lenke). Spesielt ga ligning 17 meg solenoidkraften i form av forskjellige termer.

Følgende termer var enkle å måle:

• R - Motstanden til solenoiden min
• l - Lengden på solenoiden
• x - Stempelets forskyvning i magnetventilen
• V - Spenningen over solenoiden

Jeg visste også at kraften som ble satt ut av solenoiden måtte balansere ut kraften fra 3D-trykte fjærer på speilet med to akser. Kraften til en fjær styres av Hookes lov, som er angitt som følger:

F = -kx

Selv om jeg ikke visste verdien av k, visste jeg i det minste at kraften jeg fikk ut av ligning 17 fra Schimpfs papir måtte tilsvare kraften fra Hookes lov.

Verdien av alfa (α) var vanskelig. Selv om ligning 13 og 14 viste hvordan du skal beregne disse verdiene fra området til solenoiden (A), antall svinger (N) og magnetiske permeabilitetsverdier (μ), ønsket jeg ikke å måtte rive fra hverandre en solenoid for å telle antall svinger, og jeg visste heller ikke materialet som kjernen til solenoiden min ble laget av.

Trinn 10: En rimelig komponenttester sparer dagen

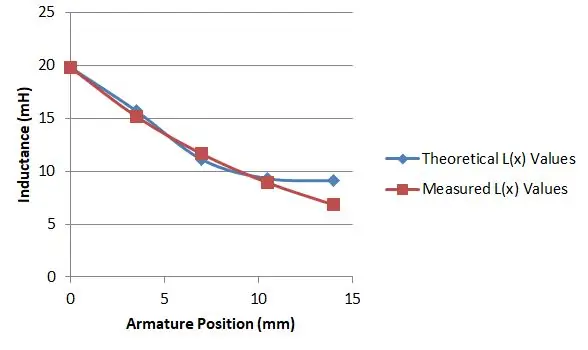
Det viste seg imidlertid at ligning 15 og 16 ga meg det jeg trengte. Jeg hadde en billig M328 komponenttester som jeg hadde kjøpt fra eBay for $ 10. Den kunne bruke den til å måle induktansen til solenoiden min, og jeg fant ut at ved å skyve ankeret inn på forskjellige dybder ga jeg forskjellige induksjonsverdier.

Å måle den med ankeret helt satt inn ga meg verdien av L (0).

Lengden på solenoiden min var 14 mm, så jeg målte induktansen med ankeret i fem stillinger, og dette ga meg forskjellige verdier for L (x):

• L (0,0) = 19,8 mH
• L (3,5) = 17,7 mH
• L (7,0) = 11,1 mH
• L (10,5) = 9,3 mH
• L (14) = 9,1 mH

Jeg brukte deretter et regneark for å plotte mine verdier mot verdien av ligning 15 og 16, for et bestemt valg av μr og deretter varierte jeg mitt valg til jeg fant en god match. Dette skjedde da μr var 2,9, som vist i grafen.

Trinn 11: Finn vårkonstant K, Løs problemet

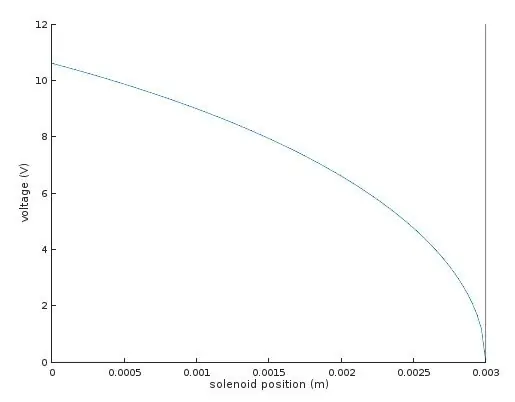
Den eneste gjenværende ukjente var K, vårkonstanten. Jeg målte dette ved å bruke 9V på en av solenoidene i min toakse-enhet og måle avstanden der speilet ble trukket ned. Med disse verdiene klarte jeg å løse ligningene for K, som jeg fant var rundt 10.41.

Jeg hadde nå verdiene jeg trengte for å beregne trekket til solenoiden i forskjellige posisjoner langs slaget. Ved å sette F (x) lik fjærkraften fra Hookes lov, kan jeg løse den nødvendige spenningen V.

Grafen viser spenningen som kreves for å flytte solenoiden til ønsket posisjon x.

Til høyre, der spenningen er null og posisjonen er 3 mm, tilsvarer dette det nøytrale hvilepunktet til solenoiden når de 3D -trykte hengslene er helt avslappet. Å bevege seg til venstre på grafen tilsvarer å trekke ankeret inn i solenoiden mot trekk av 3D-trykte hengsler-dette krever i utgangspunktet mer spenning, men etter hvert som ankeret blir dypere inn i solenoiden, øker trekket og den nødvendige drivspenningen avtar.

Dette forholdet er definitivt ikke-lineært, men med likningene fra Schimpfs papir kan jeg skrive min Arduino-kode for å sende ut riktige spenninger, slik at strålebøyningen er lineær:

float positionToVoltage (float x) {

// Gjenopprette kraft utøvd av hengsler (Hooke's Law) ved ønsket x. const float spring_F = -spring_K * (x - spring_X0); // Spenning slik at trekkraften til solenoiden samsvarer med // gjenopprettingskraften til hengslene returnerer sqrt (-2*R*R*(-spring_F)*solenoid_len/(a*L_0*exp (-a*x/solenoid_len)))); }

Dette fører til en mye mer sirkulær spiral enn i min opprinnelige bevegelsestest. Oppdrag utført!

Trinn 12: Spørsmål og svar om førerkretsen ved bruk av diskrete komponenter

Hvorfor kan jeg ikke koble solenoiden direkte til Arduino?

Det er et spørsmål om hvor mye strøm Arduino kan gi uten å påføre skade. Dette er omtrent 40mA per pinne. Når vi vet at Arduino opererer ved 5V, kan vi bruke Ohms lov til å beregne nødvendig minimumsmotstand for lasten (i dette tilfellet solenoiden). Å dele 5 volt med 0,040 ampere gir oss, 125 ohm. Hvis lasten har større motstand, kan vi koble den direkte til Arduino, ellers kan vi ikke. En liten solenoid har vanligvis en motstand på 50 ohm, så vi kan ikke kjøre den direkte fra Arduino. Hvis vi gjorde det, ville det trekke 100mA, noe som helt klart er for mye.

Hvorfor bruker du 9V for solenoiden, men 5V for Arduino?

Arduino kjører på 5V, men dette er litt for lite for en solenoid. Ved å bruke en transistor kan vi velge en spenning for solenoiden som er uavhengig av 5V som brukes til Arduino.

Hvordan vet jeg om en transistor er egnet for dette prosjektet?

Akkurat som Arduino er hovedkravet at strømmen som strømmer gjennom solenoiden ikke overstiger maksimalverdiene for transistoren (spesielt kollektorstrømmen). Vi kan enkelt beregne det verste tilfellet ved å måle motstanden til solenoiden og deretter dele forsyningsspenningen med det. Når det gjelder en 9V forsyningsstrøm for solenoider og en magnetventil på 50 ohm, setter det verste tilfellet oss til 180mA. MPS3704, for eksempel, er vurdert for en maksimal kollektorstrøm på 600 mA, noe som gir oss en margin på omtrent 3.

Hvordan bestemmer jeg minimumsverdien av motstanden som skal settes mellom Arduino -utgangen og basen til transistoren?

Utgangen fra Arduino vil koble basisbenet til de bipolare transistorene gjennom en strømbegrensende motstand. Siden Arduino opererer ved 5V, kan vi igjen bruke Ohms lov for å beregne motstanden som kreves for å begrense strømmen under 40mA. Det vil si at du deler 5 volt med 0,04 ampere for å oppnå en verdi på minst 125 ohm. Høyere motstandsverdier vil redusere strømmen, og dermed gi oss en enda større sikkerhetsmargin.

Er det en maksimal verdi for den motstanden som jeg ikke bør overskride?

Det viser seg, ja. En transistor har det som er kjent som en strømforsterkning. For eksempel, hvis forsterkningen er 100, betyr det at hvis vi setter 1mA i basen, så vil opptil 100mA strømme gjennom lasten transistoren styrer. Hvis vi setter 1,8mA inn i basen, vil opptil 180mA strømme gjennom lasten. Siden vi tidligere regnet ut at ved 9V strømmer 180mA gjennom solenoiden, så er en basestrøm på 1.8mA det "søte stedet", og mindre og solenoiden vår vil ikke slå seg på helt.

Vi vet at Arduino setter ut 5V og vi vil at 1.8mA strøm skal strømme, så vi bruker Ohms lov (R = V/I) for å beregne motstanden (R = V/I). 5V dividert med 1,8mA gir en motstand på 2777 ohm. Så gitt forutsetningene vi gjorde, forventer vi at motstanden må ligge mellom 125 og 2777 - å velge noe som 1000 ohm gir oss en ganske god sikkerhetsmargin uansett.

Trinn 13: Analyse av nåværende problemer og mulige løsninger

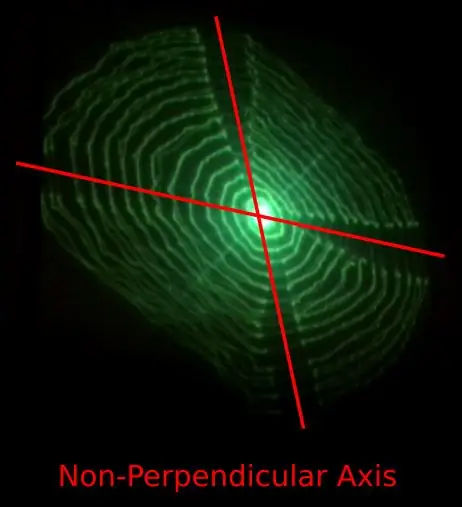
Den nåværende prototypen viser potensial, men flere problemer gjenstår:

1. Bevegelse langs X- og Y -aksen ser ikke ut til å være vinkelrett.
2. Det er et hopp når speilet endrer retning.
3. Oppløsningen er ganske lav, og det er synlige trappetrinnmønstre.
4. Ved høyere bevegelseshastigheter blir laserens bane forvrengt av vibrasjoner og ringing.

Problem 1) kan skyldes utformingen av 3D -trykte fleksible hengsler som overfører bevegelse langs en akse til den vinkelrette aksen.

Utgave 2) skyldes slakk i koblingen mellom drivstemplene og speilplattformen, dette får speilet til å rykke og hoppe ved overganger mellom X- og Y -aksen. Denne plutselige bevegelsen fører til et mørkt X -formet gap der laserprikken gjør et raskere ukontrollert trekk.

Utgave 3) oppstår fordi standard Arduino PWM bare har 255 nivåer og ganske mange av dem er bortkastet på grunn av formen på spenningskurven. Dette kan forbedres betraktelig ved bruk av timer1, som er 16-bits og som vil være i stand til 65536 unike verdier.

Utgave 4) oppstår fordi speilet og magnetventilens skyveanker (stempler) utgjør en betydelig mengde i bevegelse.

Siden problemstillingene 1) og 2) er knyttet til den mekaniske konstruksjonen, kan en mulighet være å fjerne metallstemplene og erstatte dem med små sjeldne jordartsmagneter som er festet direkte til vippeplaten. Magnetene ville være en åpen spole som ville tiltrekke eller avvise magnetene uten å komme i fysisk kontakt. Dette vil føre til jevnere bevegelse og eliminere muligheten for rykk, samtidig som total masse reduseres.

Å redusere masse er den primære løsningen for problem 4), men eventuelle gjenværende problemer kan målrettes direkte i programvare ved å implementere en bevegelseskontrollprofil i programvare for å akselerere og senke speilet på en kontrollert måte. Dette er allerede gjort mye i fastvare for 3D -skriver, og lignende metoder kan fungere også her. Her er noen ressurser knyttet til bevegelseskontroll slik den gjelder for 3D -skrivere:

• "Mathematics of Motion Control Profiles", Chuck Lewin (lenke)
• "Jerk Controlled Motion Explained", (lenke)

Jeg mistenker at ved å legge til en trapezformet bevegelseskontrollprofil kan speilet kjøres med mye høyere hastigheter uten ringing eller vibrasjonsartefakter.

Trinn 14: Fremtidig arbeid og mulige applikasjoner

Selv om det vil ta mye arbeid å utvikle løsninger på disse problemene, håper jeg at denne modulen med åpen kildebjelke kan bli et rimelig alternativ til galvanometerbaserte prosjekter i slike applikasjoner som:

• Et rimelig lasershow for DJ -er og VJ -er.
• En elektromekanisk vektordisplay for et vintage arkadespill som Vectrex.
• En DIY harpiks-type SLA 3D-skriver som i ånden til RepRap-bevegelsen kan skrive ut sin egen laserstyringsmodul.
• Digital panorering eller optisk bildestabilisering for kameraer.

Andre pris i Arduino -konkurransen 2017