Solsystemsimulering: 4 trinn

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-30 11:24

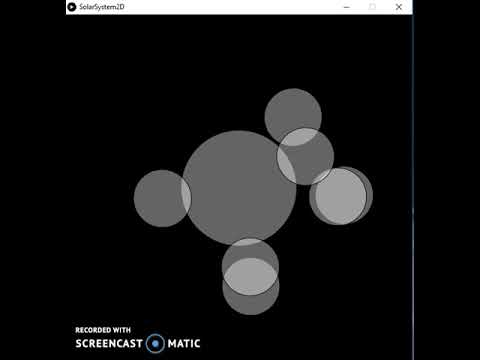
For dette prosjektet satte jeg meg for å lage en simulering av hvordan tyngdekraften påvirker bevegelsen til planetariske kropper i et solsystem. I videoen ovenfor / er sollegemet representert av trådmasken, og planetene genereres tilfeldig.

Planetenes bevegelse er basert på ekte fysikk, loven om universell gravitasjon. Denne loven definerer gravitasjonskraften som utøves på en masse av en annen masse; i dette tilfellet Solen på alle planetene, og planetene på hverandre.

For dette prosjektet brukte jeg Processing, et java -basert programmeringsmiljø. Jeg brukte også Processing -eksempelfilen som simulerer planetenes tyngdekraft. Alt du trenger for dette er behandlingsprogramvaren og en datamaskin.

Trinn 1: 2 dimensjonal simulering

Jeg begynte med å se på noen videoer om hvordan du kan kode dette som Dan Shiffman opprettet på sin YouTube -kanal, Coding Train (del 1/3). På dette tidspunktet tenkte jeg at jeg ville bruke rekursjon for å generere solsystemet, på samme måte som Shiffman bare bruker fysikklovene.

Jeg skapte et planetobjekt som hadde "barnplaneter", som igjen også hadde "barn" -planeter. Koden for 2D -simuleringen var ikke ferdig fordi jeg ikke hadde en flott måte å simulere gravitasjonskreftene for hver planet. Jeg svingte fra denne tankegangen, i en retning basert på det innebygde behandlingseksemplet på gravitasjonsattraksjon. Problemet var at jeg trengte å beregne gravitasjonskraften fra alle de andre planetene på hver planet, men kunne ikke tenke på hvordan jeg kunne trekke informasjonen til en individuell planet lett. Etter å ha sett hvordan behandlingsopplæringen gjør det, skjønte jeg nøyaktig hvordan jeg skulle gjøre det ved hjelp av løkker og matriser i stedet

Trinn 2: Ta den til 3 dimensjoner

Ved å bruke eksempelkoden for Planetary Attraction som følger med behandling, startet jeg et nytt program for en 3D -simulering. Den største forskjellen er i Planet -klassen, der jeg la til en tiltrekningsfunksjon, som beregner gravitasjonskraften mellom to planeter. Dette tillot meg å simulere hvordan solsystemene våre fungerer, hvor planetene ikke bare tiltrekkes av solen, men også av alle andre planeter.

Hver planet har tilfeldig genererte egenskaper som masse, radius, innledende banehastighet, osv. Planetene er solide sfærer og solen er en trådmaske. I tillegg roterer kameraposisjonen rundt midten av vinduet.

Trinn 3: Bruke virkelige planeter

Etter at jeg fikk rammene for 3D -simuleringen nede, brukte jeg Wikipedia til å finne de faktiske planetdataene for vårt solsystem. Jeg opprettet en rekke planetobjekter og legger inn de virkelige dataene. Da jeg gjorde dette, måtte jeg nedskalere alle egenskapene. Da jeg gjorde dette burde jeg ha tatt de faktiske verdiene og multiplisert med en faktor for å skalere ned verdiene, i stedet gjorde jeg det i enheter av jordene. Det vil si at jeg tok forholdet Jordas verdi til de andre objektenes verdi, for eksempel har solen 109 ganger mer masse enn jorden. Dette resulterte imidlertid i at størrelsene på planetene så for store eller for små ut.

Trinn 4: Avsluttende tanker og kommentarer

Hvis jeg skulle fortsette å jobbe med denne simuleringen, ville jeg finjustere/forbedre et par ting:

1. Først ville jeg skalere alt jevnt med den samme skaleringsfaktoren. For å forbedre synligheten til banene vil jeg legge til et spor bak hver planet for å se hvordan hver revolusjon kan sammenlignes med den forrige

2. Kameraet er ikke interaktivt, noe som betyr at en del av banene er utenfor skjermen, "bak personen". Det er et 3D -kamerabibliotek kalt Peazy Cam, som brukes på del 2 av Coding Train's videoserie om dette emnet. Dette biblioteket lar betrakteren rotere, panorere og zoome kameraet slik at de kan følge hele bane på en planet.

3. Til slutt er planetene foreløpig umulige å skille fra hverandre. Jeg vil gjerne legge til «skinn» til hver planet og Solen, slik at seerne kan kjenne igjen jorden og slikt.