Løse sannhetstabeller: 10 trinn

2025 Forfatter: John Day | [email protected]. Sist endret: 2025-01-23 15:02

En sannhetstabell er en måte å visualisere alle resultatene av et problem. Dette instruksjonssettet er laget for folk som kommer i gang med diskret matematikk. Vi skal øve i dag med et eksempelproblem som er spesifikt for disse instruksjonene. Du trenger litt skrapepapir og en blyant for å visualisere bordet. Dette problemet bør ta rundt 5 minutter å fullføre for personer med forkunnskaper om emnet og rundt 10 minutter for nybegynnere.

For dette instruksjonssettet vil vi fokusere på problemet ~ p Λ q. Vi bruker dette til å introdusere noen symboler som trengs for å tolke sannhetstabeller.

Trinn 1: Forstå sannhetstabeller

En sannhetstabell er en måte å visualisere alle mulighetene for et problem. Å kjenne sannhetstabeller er en grunnleggende nødvendighet for diskret matematikk. Her finner vi alle resultatene for den enkle ligningen ~ p Λ q.

Trinn 2: Å kjenne symbolene

Det første trinnet til sannhetstabellen er å forstå tegnene. "~" I dette spesielle problemet står for negasjon. "P" og "q" er begge variabler. "Λ" tilsvarer "og". Denne ligningen leses som "ikke p og q", noe som betyr at ligningen er sann hvis p ikke er sant og q er sant.

Trinn 3: Formatering av tabellen

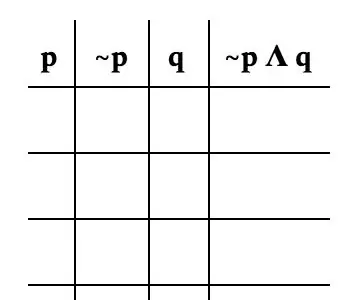
Nå for å danne det faktiske bordet. Det er viktig å dele opp problemet med hver variabel. For dette problemet vil vi dele det opp som følger: p, ~ p, q, og ~ p Λ q. Bildet er et godt eksempel på hvordan bordet ditt skal se ut.

Trinn 4: Tilordne sant og usant

Siden det bare er to variabler, vil det bare være fire muligheter per variabel. For p deler vi det opp med halvparten av mellomrommene tatt av T (for sant) og den andre halvdelen med F (for usann).

Trinn 5: Negasjon

For ~ p skriver du det motsatte tegnet som p har siden ~ p er det motsatte av p.

Trinn 6: Variabel "q"

For q veksler du mellom T og F for å få hver mulig kombinasjon. Siden ligningen bare fokuserer på ~ p, kan vi ignorere p -kolonnen når vi skal bestemme sannheten i ligningen. “Λ” -symbolet betyr at både ~ p og q må være sanne for at ligningen skal være sann.

Trinn 7: Løse feil i siste kolonne

For den første raden, siden ~ p er F og q er T, ~ p Λ q er F i scenariet som ~ p er F og q er T. Det eneste scenariet ligningen er T er hvor ~ p er T og q er T.

Trinn 8: Finne det sanne i den siste kolonnen

Dette betyr at den eneste raden som er T er den tredje.

Trinn 9: Fullfør tabellen

Dobbeltsjekk at bordet ditt er riktig. Du gjør dette ved å kontrollere at skiltene dine er riktige og sørge for at den siste kolonnen er gjort riktig. Den siste kolonnen er resultatet av alle mulige permutasjoner fra variablene.

Trinn 10: Ferdig

Nå som du vet hvordan du gjør et grunnleggende sannhetstabell, fortsett å øve! Jo mer du øver, jo bedre blir du til å gjøre dem.