Innholdsfortegnelse:
- Trinn 1: Utvid det dynamiske området for bildet eller bildene dine
- Begrunnelse:
- Trinn 2: Behandle bildene, eller utfør datamaskinvisjonen, maskinlæring eller lignende
- Trinn 3: Komprimer det dynamiske området for resultatet på nytt
- Trinn 4: Du vil kanskje prøve noen andre varianter
- Trinn 5: Gå videre: Prøv det nå med HDR -bildekompositter
- Forfatter John Day day@howwhatproduce.com.
- Public 2024-01-30 11:24.
- Sist endret 2025-01-23 15:02.
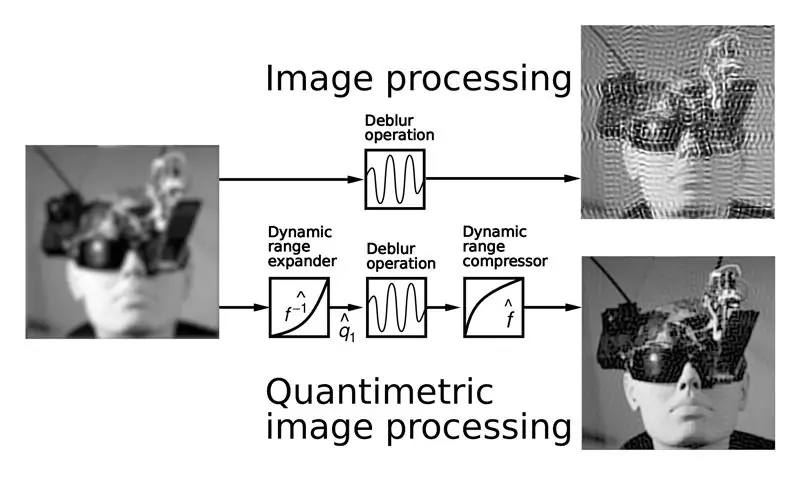



(Figuren over illustrerer sammenligning av eksisterende bildebehandlingsmetode med kvantimetrisk bildebehandling. Legg merke til det forbedrede resultatet. Bilde øverst til høyre viser merkelige artefakter som kommer fra feil antagelse om at bilder måler noe som lys. Bilde nederst til høyre viser bedre resultat ved å gjøre det samme kvantimetrisk.)
I denne instruksjonsboken lærer du hvordan du kan forbedre ytelsen til eksisterende bilde- eller synsføler systemer ved å bruke et veldig enkelt konsept: Kvantimetrisk bildesensering
Kvantimetrisk bildebehandling forbedrer kraftig på noe av følgende:
- Eksisterende bildebehandling som for eksempel sløring av bilder;
- Maskinlæring, datasyn og mønstergjenkjenning;
- Bærbar ansiktsgjenkjenning (se https://wearcam.org/vmp.pdf), AI og HI -basert visjon, etc.
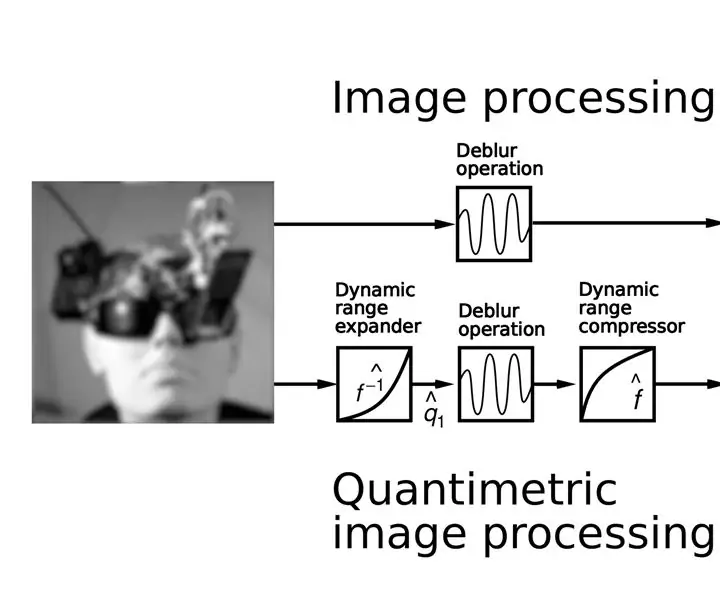
Grunnideen er å kvantimetrisk forbehandle og etterbehandle bildene, som følger:
- Utvid det eller de dynamiske områdene til bildet eller bildene;
- Behandle bildet eller bildene som du normalt ville gjort;
- Komprimer det dynamiske området til bildet eller bildene (dvs. angre trinn 1).
I tidligere instrukser lærte jeg noen aspekter ved HDR -sensing (High Dynamic Range) og kvantimetrisk sansing, f.eks. linearitet, superposisjon, etc.
La oss nå ta denne kunnskapen i bruk.
Ta en eksisterende prosess du vil bruke. Eksemplet jeg vil vise er sløring av bilder, men du kan også bruke det til omtrent alt annet.
Trinn 1: Utvid det dynamiske området for bildet eller bildene dine
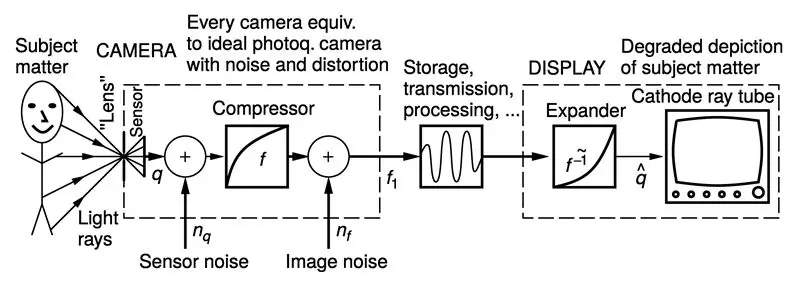
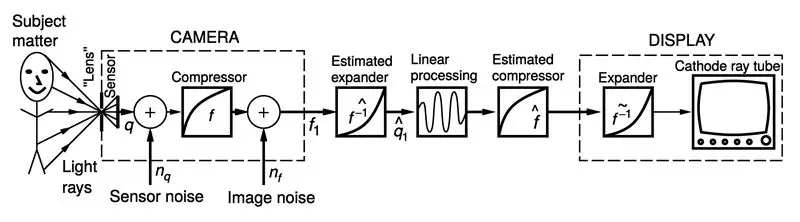
(Figurer tilpasset fra "Intelligent Image Processing", John Wiley and Sons Interscience Series, Steve Mann, november 2001)
Det første trinnet er å utvide det dynamiske området til inngangsbildet.
Ideelt sett bør du først bestemme kameraets responsfunksjon, f, og deretter bruke den inverse responsen, f invers, på bildet.
Typiske kameraer er komprimerende for dynamisk område, så vi ønsker vanligvis å bruke en ekspansiv funksjon.
Hvis du ikke kjenner svarfunksjonen, kan du begynne med å prøve noe enkelt, for eksempel å laste inn bildet i et bildearray, kaste variablene til en datatype som (float) eller (double) og øke hver pikselverdi til en eksponent, for eksempel som å kvadrere hver pikselverdi.
Begrunnelse:
Hvorfor gjør vi dette?
Svaret er at de fleste kameraer komprimerer sitt dynamiske område. Grunnen til at de gjør dette er at de fleste displaymedier utvider det dynamiske området. Dette er ganske tilfeldig: lysmengden fra et katodestrålerør er omtrent lik spenningen som er hevet til eksponenten 2,22, slik at når videospenninginngangen er omtrent halvveis, er mengden lys som slippes ut mye mindre enn halvparten.
Fotografiske medier er også ekspansive med dynamisk rekkevidde. For eksempel avgir et fotografisk "nøytralt" grått kort 18% av det innfallende lyset (ikke 50% av det innfallende lyset). Dette mye lys (18%) anses å være midt i responsen. Så som du kan se, hvis vi ser på en utgangsgraf som en funksjon av input, oppfører displaymedier seg som om de er ideelle lineære skjermer som inneholder en dynamisk rekkeviddeekspander før den ideelle lineære responsen.
I den øverste figuren ovenfor kan du se displayet innrammet med en stiplet linje, og det tilsvarer å ha en ekspander før den ideelle lineære skjermen.
Siden skjermer iboende er ekspansive, må kameraene utformes for å være komprimerende slik at bildene ser bra ut på de eksisterende skjermene.
Tilbake i gamle dager da det var tusenvis av TV -mottakerskjermer og bare en eller to kringkastingsstasjoner (f.eks. Bare ett eller to fjernsynskameraer), var det en enklere løsning å sette en komprimerende ikke -linearitet inn i kameraet enn å huske alle fjernsynene og legg en i hver fjernsynsmottaker.
Ved et uhell hjalp dette også med støydemping. I lyd kaller vi dette "Dolby" ("companding") og tildeler patent på det. I video skjedde det helt tilfeldig. Stockham foreslo at vi skulle ta logaritmen til bilder før vi behandler dem, og deretter ta antiloggen. Det han ikke innså er at de fleste kameraer og skjermer allerede gjør dette ganske tilfeldig. I stedet er det jeg foreslo at vi gjør det stikk motsatte av det Stockham foreslo. (Se "Intelligent bildebehandling", John Wiley and Sons Interscience Series, side 109-111.)
I det nedre bildet ser du den foreslåtte anti-homomorfe (kvantimetriske) bildebehandlingen, der vi har lagt til trinnet med ekspansjon og komprimering av det dynamiske området.
Trinn 2: Behandle bildene, eller utfør datamaskinvisjonen, maskinlæring eller lignende
Det andre trinnet, etter utvidelse av dynamisk område, er å behandle bildene.
I mitt tilfelle utførte jeg ganske enkelt en dekonvolusjon av bildet, med uskarphetsfunksjonen, dvs. bildesløring, som det er kjent i teknikken.
Det er to brede kategorier av kvantimetrisk bildesensering:
- Å hjelpe folk å se;
- Hjelper maskiner med å se.
Hvis vi prøver å hjelpe folk med å se (som er eksemplet jeg viser her), er vi ikke ferdige ennå: Vi må ta det behandlede resultatet tilbake til bilderommet.
Hvis vi hjelper maskiner med å se (f.eks. Ansiktsgjenkjenning), er vi ferdige nå (du trenger ikke å gå videre til trinn 3).
Trinn 3: Komprimer det dynamiske området for resultatet på nytt
Når vi jobber i et utvidet dynamisk område, sies vi å være i "lysrom" (kvantimetrisk bilderom).
På slutten av trinn 2 er vi i lysrom, og vi må komme tilbake til bilderommet.
Så dette trinn 3 handler om å komme tilbake til bilderommet.
For å utføre trinn 3, komprimerer du bare det dynamiske området for utgangen fra trinn 2.
Hvis du kjenner svarfunksjonen til kameraet, kan du bare bruke den for å få resultatet, f (p (q)).
Hvis du ikke kjenner svarfunksjonen til kameraet, må du bare gjette.
Hvis du kvadrerte bildepikslene i trinn 1, er det nå på tide å ta kvadratroten til hver bildepiksel for å komme tilbake til gjetningen din om bilderommet.
Trinn 4: Du vil kanskje prøve noen andre varianter
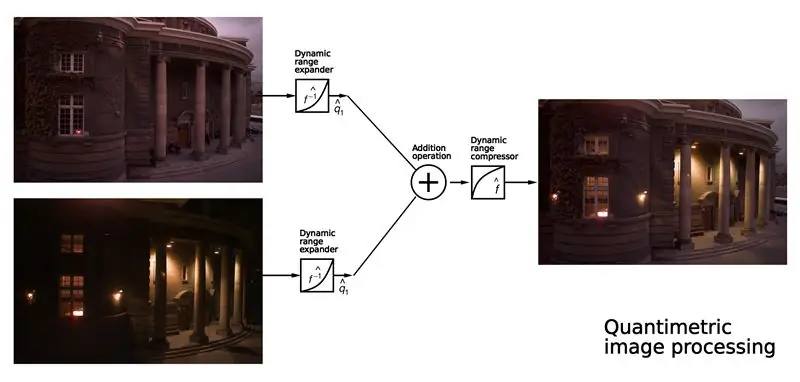



Deblurring er bare ett av mange mulige eksempler. Tenk for eksempel på kombinasjonen av flere eksponeringer.
Ta to bilder, for eksempel de to jeg har ovenfor. Den ene ble tatt i løpet av dagen, og den andre om natten.
Kombiner dem for å lage et skumringslignende bilde.
Hvis du bare gjennomsnitt dem sammen, ser det ut som søppel. Prøv dette selv!
Men hvis du først utvider det dynamiske området til hvert bilde, legger til dem og deretter komprimerer det dynamiske området til summen, ser det bra ut.
Sammenlign bildebehandling (legge til bildene) med kvantimetrisk bildebehandling (utvide, legge til og komprimere deretter).
Du kan laste ned koden min og mer eksempelmateriale herfra:
Trinn 5: Gå videre: Prøv det nå med HDR -bildekompositter

(Over bildet: HDR -sveisehjelm bruker kvantimetrisk bildebehandling for augmented reality -overlegg. Se Slashgear 2012 12. september)
Oppsummert:
ta et bilde, og bruk følgende trinn:
- utvide det dynamiske området til bildet;
- behandle bildet;
- komprimere det dynamiske området til resultatet.
Og hvis du vil ha et enda bedre resultat, kan du prøve følgende:
fange en rekke forskjellige eksponerte bilder;
- utvide det dynamiske området til lysrom, i henhold til min tidligere Instructable on HDR;
- behandle det resulterende kvantimetriske bildet, q, i lysrom;
- komprimere det dynamiske området gjennom tonemapping.
Ha det gøy, og klikk "Jeg klarte det" og legg ut resultatene, så kommenterer jeg gjerne eller gir konstruktiv hjelp.
Anbefalt:
Arduino bilvarslingssystem for omvendt parkering - Trinn for trinn: 4 trinn

Arduino Car Reverse Parking Alert System | Trinn for trinn: I dette prosjektet skal jeg designe en enkel Arduino Car Reverse Parking Sensor Circuit ved hjelp av Arduino UNO og HC-SR04 Ultrasonic Sensor. Dette Arduino -baserte bilreverseringssystemet kan brukes til autonom navigasjon, robotavstand og andre områder
Bildebehandling med Raspberry Pi: Installering av OpenCV og bildefargeseparasjon: 4 trinn

Bildebehandling med Raspberry Pi: Installere OpenCV og bildefargeseparasjon: Dette innlegget er det første av flere opplæringsprogrammer for bildebehandling som skal følge. Vi ser nærmere på pikslene som utgjør et bilde, lærer hvordan du installerer OpenCV på Raspberry Pi, og vi skriver også testskript for å ta et bilde og også
DIY termisk bildebehandling infrarødt kamera: 3 trinn (med bilder)
DIY Thermal Imaging Infrared Camera: Hei! Jeg leter alltid etter nye prosjekter for fysikkundervisningen min. For to år siden kom jeg over en rapport om termosensoren MLX90614 fra Melexis. Den beste med bare 5 ° FOV (synsfelt) ville være egnet for et selvlaget termisk kamera. Å lese
En introduksjon til bildebehandling: Pixy og dens alternativer: 6 trinn

En introduksjon til bildebehandling: Pixy og dets alternativer: I denne artikkelen vil vi forklare betydningen av Digital Image Processing (DIP) og årsakene til å bruke maskinvare som Pixy og andre verktøy for å lage en prosess på bilder eller videoer. På slutten av denne artikkelen lærer du: Hvordan et digitalt bilde dannes
Moyamoya Bildebehandling: 8 trinn
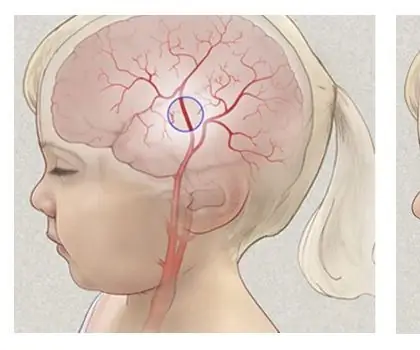
Moyamoya Bildebehandling: Moyamoya, "røykpust", " er en sjelden sykdom som skyldes blokkering av arterier ved basalganglier, som er et område ved hjernebunnen. Sykdommen er en progressiv cerebrovaskulær sykdom som for det meste rammer barn. Sym
