Innholdsfortegnelse:
- Forfatter John Day day@howwhatproduce.com.
- Public 2024-01-30 11:23.
- Sist endret 2025-01-23 15:02.



Hallo!
For denne fysikk-enheten trenger du:
* en strømforsyning med 0-12V
* en eller flere kondensatorer
* en eller flere lademotstander
* en stoppeklokke
* et multimeter for spenningsmåling
* en arduino nano
* en 16x2 I²C -skjerm
* 1 / 4W motstander med 220, 10k, 4.7M og 1Gohms 1 gohms motstand
* dupont wire
Trinn 1: Generell informasjon om kondensatorer




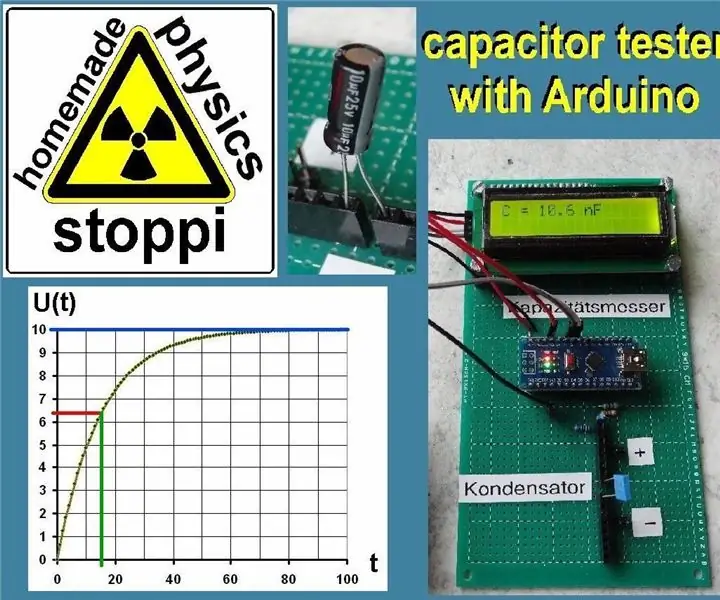
Kondensatorer spiller en veldig viktig rolle i elektronikk. De brukes til å lagre ladninger, som et filter, integrator, etc. Men matematisk er det mye i kondensatorer. Så du kan øve eksponentielle funksjoner med kondensatorer og de. trene. Hvis en opprinnelig uladet kondensator er koblet via en motstand til en spenningskilde, strømmer ladningene kontinuerlig til kondensatoren. Med den økende ladningen Q, i henhold til formelen Q = C * U (C = kondensatorens kapasitans), øker også spenningen U over kondensatoren. Ladestrømmen avtar imidlertid mer og mer etter hvert som den hurtigladede kondensatoren blir vanskeligere og vanskeligere å fylle med ladninger. Spenningen U (t) på kondensatoren følger følgende formel:
U (t) = U0 * (1-eksp (-k * t))
U0 er spenningen til strømforsyningen, t er tiden og k er et mål på hastigheten på ladeprosessen. Hvilke størrelser er k avhengig av? Jo større lagringskapasitet (det vil si kondensatorens kapasitans C), jo langsommere fylles den med ladninger og jo langsommere øker spenningen. Jo større C, jo mindre k. Motstanden mellom kondensator og strømforsyning begrenser også ladningstransport. En større motstand R forårsaker en mindre strøm I og derfor strømmer færre ladninger per sekund til kondensatoren. Jo større R, jo mindre k. Det riktige forholdet mellom k og R eller C er:
k = 1 / (R * C).
Spenningen U (t) ved kondensatoren øker dermed i henhold til formelen U (t) = U0 * (1-eksp (-t / (R * C)))
Trinn 2: Målingene




Elevene skal angi spenningen U på tidspunktet t i en tabell og deretter tegne den eksponentielle funksjonen. Hvis spenningen øker for fort, må du øke motstanden R. På den andre siden, hvis spenningen endres for sakte, reduserer du R.
Hvis man kjenner U0, motstanden R og spenningen U (t) etter en viss tid t, kan kondensatorens kapasitans C beregnes ut fra dette. For dette må man logaritme ligningen, og etter noen transformasjoner får vi: C = -t / (R * ln (1 - U (t) / U0))
Eksempel: U0 = 10V, R = 100 kohms, t = 7 sekunder, U (7 sek) = 3,54V. Da resulterer C i en verdi på C = 160 μF.
Men det er en annen, enkel metode for å bestemme kapasiteten C. Nemlig er spenningen U (t) etter t = R * C nøyaktig 63,2% av U0.
U (t) = U0 * (1-eksp (-R * C / (R * C)) = U0 * (1-eksp (-1)) = U0 * 0,632
Hva betyr dette? Elevene må bestemme tiden t hvorpå spenningen U (t) er nøyaktig 63,2% av U0. Spesifikt, for eksemplet ovenfor, søkes tiden etter hvor spenningen over kondensatoren er 10V * 0,632 = 6,3V. Dette er tilfellet etter 16 sekunder. Denne verdien er nå satt inn i ligningen t = R * C: 16 = 100000 * C. Dette gir resultatet: C = 160 μF.
Trinn 3: Arduino



På slutten av øvelsen kan kapasiteten også bestemmes med en Arduino. Dette beregner kapasiteten C nøyaktig i henhold til tidligere metode. Den lader kondensatoren via en kjent motstand R med 5V og bestemmer tiden etter hvilken spenningen ved kondensatoren = 5V * 0,632 = 3,16V. For Arduino digital-til-analog-omformeren er 5V lik 1023. Derfor er det bare å vente til verdien på den analoge inngangen er 1023 * 3,16 / 5 = 647. Med denne tiden kan kapasiteten C beregnes. For at kondensatorer med svært forskjellig kapasitans kan måles, brukes 3 forskjellige lademotstander. Først brukes en lav motstand for å bestemme ladetiden opp til 647. Hvis denne er for kort, dvs. hvis kondensatorens kapasitans er for liten, velges neste høyere ladningsmotstand. Hvis dette også er for lite, følger en 1 Gohms -motstand på slutten av målingen. Verdien for C vises deretter på displayet med riktig enhet (µF, nF eller pF).
Trinn 4: Konklusjoner

Hva lærer elevene i denne enheten? Du vil lære om kondensatorer, deres kapasitans C, eksponensielle funksjoner, logaritme, prosentvise beregninger og Arduino. Jeg tenker mye.
Denne enheten er egnet for studenter i alderen 16-17 år. Du må allerede ha gått gjennom den eksponensielle funksjonen og logaritmen i matematikk. Ha det gøy å prøve det i klassen din og Eureka!
Jeg ville være veldig glad hvis du ville stemme på meg i klasseromsvitenskapskonkurransen. Tusen takk for dette!
Hvis du er interessert i mine andre fysikkprosjekter, her er min YouTube -kanal:
flere fysikkprosjekter:
Anbefalt:
555 kondensatortester: 4 trinn (med bilder)

555 kondensatortester: Dette er noe jeg bygde fra en publisert skjematisk sent på 1980 -tallet. Det fungerer veldig bra. Jeg ga bort bladet med skjematikken fordi jeg trodde jeg aldri ville trenge det igjen, og vi reduserte. Kretsen er bygget rundt en 555 timer. T
Arduino Nano kapasitansmåler: 8 trinn (med bilder)
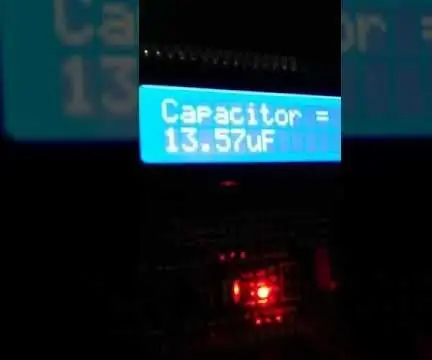
Arduino Nano Capacitance Meter: Dette prosjektet er praktisk talt tre komponenter fordi det er dannet av en 16X2 LCD -skjerm, et potensiometer 10K og en Arduino Nano mens resten av delene er en PCB designet av meg ved hjelp av EasyEda -programvare, 1 X 40 HEADER, 0.1 " PLASS, og 1x6 FEMAL
Kapasitansmåler med TM1637 ved bruk av Arduino .: 5 trinn (med bilder)

Kapasitansmåler med TM1637 ved bruk av Arduino .: Hvordan lage en kapasitansmåler ved hjelp av Arduino som vises på TM1637. Fra 1 uF til ca 2000 uF
Third Hand ++: en flerbrukshjelpende hånd for elektronikk og annet delikat arbeid. 14 trinn (med bilder)

Third Hand ++: en flerbrukshjelpende hånd for elektronikk og annet delikat arbeid.: Tidligere har jeg brukt de tredje hendene/hjelpende hendene som er tilgjengelig i kjedeelektronikkbutikker og har blitt frustrert over brukervennligheten. Jeg kunne aldri få klippene akkurat der jeg ville ha dem, eller det tok mer tid enn det egentlig burde konfigurere
En enkel å lage, billig og enkel LED-blinkende krets med CMOS 74C14: 5 trinn

En enkel å lage, billig og enkel LED-blinkende krets med CMOS 74C14: Noen ganger trenger du ganske enkelt noen blinkende lysdioder, for dekorasjon av chrismas, blinkende kunstverk eller bare for å ha det gøy med blink blink blink. Jeg skal vise deg hvordan du lager en billig og enkel krets med opptil 6 blinkende lysdioder. Merk: Dette er min første instuctable og
