2-knappers kvadratisk ligningsløser: 5 trinn

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-30 11:22

Introduksjon

Velkommen til min første instruks!

Jeg startet dette prosjektet for å utvide min programmeringskunnskap. Ofte slår du bare sammen en annen kildekode for å lage programmet du trenger. Målet mitt var å skrive min egen programkode for samhandling med et verktøy. Jeg likte å lage et enkelt verktøy for beregning. For noen måneder siden støttet jeg en venn for å løse kvadratisk ligning.

Bazinga! dette er brukstilfellet!

Jeg brukte en gammel metallboks på nytt. Jeg foretrakk det minimalistiske utseendet og grensesnittet til verktøy. det er grunnen til at jeg bare vil bruke to knapper for å gi input. Kampen vil bli vist med en enkel LCD -skjerm.

Rekvisita

materialeliste:

eske

Arcade -stil med 2 knapper

Arduino Nano, eller lignende

LCD -skjerm 1602 med I2C -adapter

På / av bryter

ledninger

2x 10k Ohm motstand

batteri 9v blokk

kontakt for 9v batteri

brødbrett

diverse (treverk, metallvinkel, kabelbindere, skruer, skiver)

verktøy:

sag

loddejern

drill maskin

datamaskin for programmering

Trinn 1: Matematisk bakgrunn

Matematisk bakgrunn

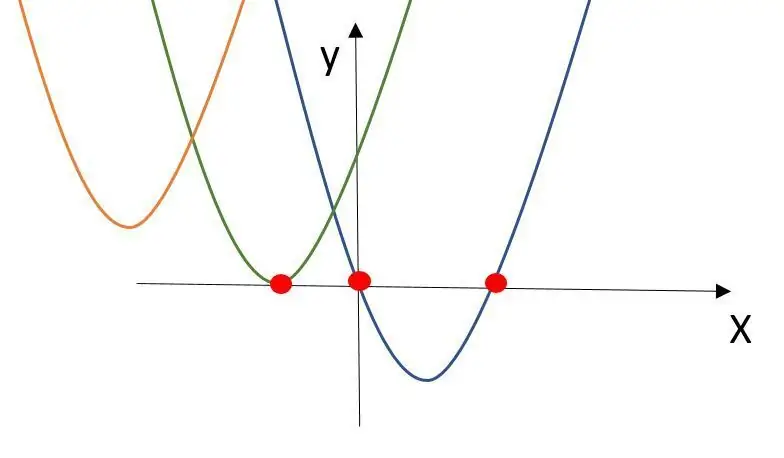
Den 2-knappers kvadratiske ligningen viser verdiene der den kvadratiske funksjonen krysser X-aksen. En kvadratisk funksjon kan krysse X-aksen aldri, en eller to ganger.

Det er forskjellige måter å beregne disse verdiene på. For verktøyet mitt bruker jeg PQ-formelen (jeg er ikke sikker på om dette uttrykket vil bli brukt over hele verden).

En kvadratisk ligning har formen:

ax²+bx+c = 0

For å beregne kryssingspunktene deler du skjemaet med a x²+px+q = 0 med p = b/a; q = c/a

PQ -formelen:

x1 = -p/2 + sqrt ((p/2) ² -q)

x2 = -p/2 -sqrt ((p/2) ² -q)

Resultatet x kan få 0, 1 eller 2 verdier. Det avhenger av verdien under kvadratroten.

Er verdien> 0, så har PQ-formelen to løsninger.

Er verdien = 0, så har PQ-formelen en løsning

er verdien <0, så har PQ -formelen ingen løsning. Funksjonen krysser ikke X-aksen.

Trinn 2: Programvare

Programvare

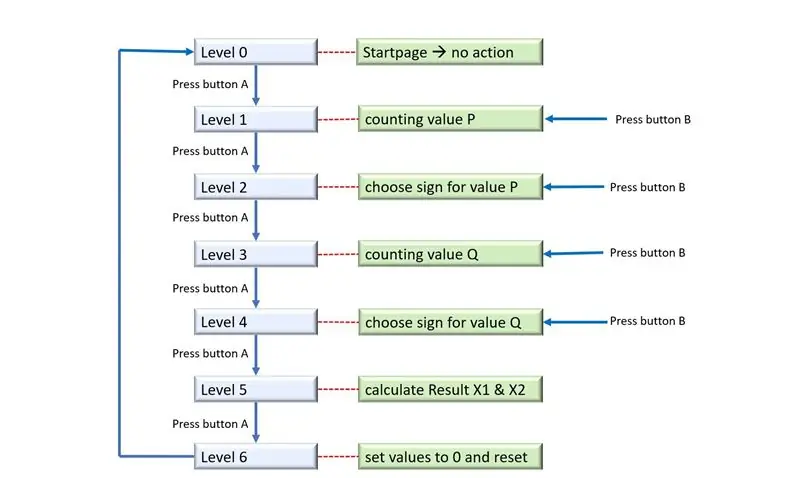
For programmering brukte jeg den offisielle Arduino IDE. Målet mitt var å lage mitt eget program. Grensesnittet mitt skal ha to knapper. En knapp for å gå mellom forskjellige nivåer, den andre knappen for å endre verdiene i de forskjellige nivåene.

For å løse PQ-formelen, lager jeg strukturen ovenfor:

Sikkert, jeg finner ikke opp hjulet på nytt. For å lage koden brukte jeg modulen:

- debounce

- vise

Følgende punkter var de største utfordringene:

- Hvordan kan jeg velge skiltet? Jeg løste denne utfordringen med funksjonen modulo (lenke). Koden deler inngangen med 2. Er inngangen et oddetall, verdien blir negativ, ellers er tallet positivt.

- Etter å ha kjørt gjennom alle nivåer, må jeg deklarere alle verdier til 0.

- Den viste teksten sletter bare sendetegnene. Hvis kodene sender et ord med 4 tegn, blir bare disse 4 tegnene lastet inn på nytt. Hvis ordet før hadde flere tegn, forblir tegnene. For å fikse det, blir den viste teksten fylt opp med tomrom. Alle de 16 tegnene på rad blir lastet inn på nytt.

Den endelige koden er vedlagt.

Trinn 3: Maskinvare

Maskinvare

Delene er listet opp ovenfor. For dette prosjektet er maskinvaren enkel. Jeg trenger bare en Arduino mikroprosessor, 2 knapper og en skjerm. Ok, hvis du liker å sette i en eske, trenger du også en eske og strømforsyning.

Jeg bruker en gammel metallboks på nytt. Jeg boret et hull i knappen for å koble til bryteren for strømforsyning. Bokslokket har 3 hull. Jeg boret to hull for de store knappene og kuttet et vindu for displayet. Jeg stikker et lite treverk bak omslaget for å ha flere ting å fikse display og knapper. For å oppgradere utseendet fikk esken klistremerker.

For strømforsyning anbefaler jeg oppladbare 9V blokkbatterier. Jeg kobler batteriet via strømbryteren til Arduino. Batteriet er festet til esken med en liten metallvinkel. Kontakten til batteriet er bare festet med kabelbindere.

Mikroprosessoren er en klon av en Arduino nano. For denne brukstilfellet er ytelsen tilstrekkelig. En Attiny 85, for eksempel en Digispark -mikroprosessor, ble avvist. Arduinoen er "brødbrettet" ved siden av skjermen.

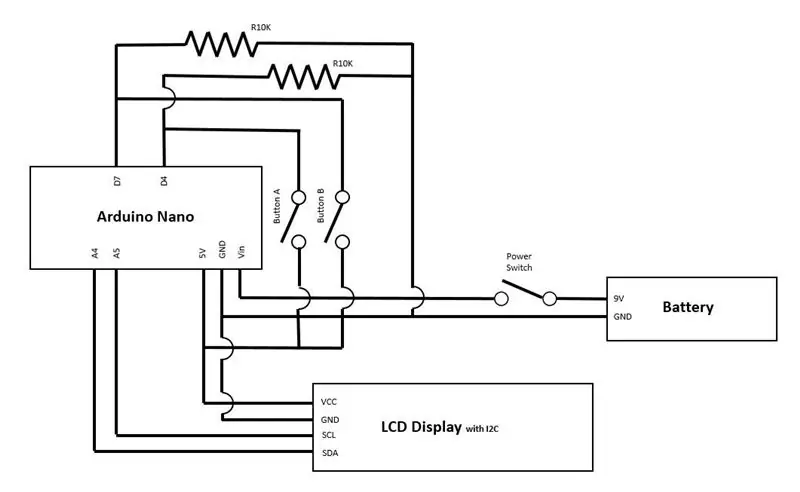
Skjermen er en 1602 LCD -skjerm. du kan bruke 16 tegn i to rader. Du kan finne denne skjermen i mange forskjellige maskiner og verktøy. Det er to forskjellige måter å bruke denne skjermen på. Du kan koble skjermen direkte til kontrolleren, eller du kan bruke et tillegg for å kommunisere med skjermen via I2C. I2C er en standard protokoll. Jeg brukte den, fordi det er lettere å koble skjermen til kontrolleren. Du trenger bare 4 kabler i stedet for 16, VCC til 5V, GND til GND, SDA til A4, SCL til A5. Displayet er festet med skruer til boksdekselet.

Knappene er enorme! de har den typiske arkadespillstilen. Jeg liker det! Knappene er koblet til digital pin 4 og 7. Ikke glem 10K motstandene!

For å åpne dekselet, for eksempel for å bytte batteri, brukte jeg lengre kabler som var koblet til brødbrettet.

Trinn 4: Kabling

Trinn 5: Framtidig forbedring

Framtidig forbedring

Etter at du har fullført et prosjekt, finner du alltid feil eller funksjoner som kan forbedres. I dette prosjektet er jeg glad for å bare finne noen få punkter, jeg ville forbedre for fremtiden.

For neste gang ville jeg forbedre utnyttelsen i boksen. Jeg fikset skjermen, strømbryteren og knappene i begynnelsen av dette prosjektet. På slutten fikk jeg litt problemer med å finne nok plass til batteriet og mikroprosessoren i esken. Når jeg plasserte knappen og displayet mer utenfor, ville jeg ikke ha noen problemer med plass til delene inne i esken.

For øyeblikket har jeg ingen brukstilfelle for å løse kvadratisk ligning. For å forbedre verktøyet, vil jeg utvide verktøyet med ytterligere matematiske ting, for eksempel grunnleggende beregning eller formler som binominell formel eller setning til Pythagoras.