Selvbalanserende robot ved bruk av PID -algoritme (STM MC): 9 trinn

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-30 11:24

Nylig har det blitt gjort mye arbeid med selvbalansering av objekter. Konseptet med selvbalansering startet med balansering av omvendt pendel. Dette konseptet utvidet seg også til design av fly. I dette prosjektet har vi designet en liten modell av selvbalanserende robot ved bruk av PID (Proportional, Integral, Derivative) algoritme. Siden den gang er denne metoden det nye ansiktet til industrielle prosesskontrollsystemer. Denne rapporten gjennomgår metodene som er involvert i selvbalansering av objekter. Dette prosjektet ble gjennomført som et semesterprosjekt for å forstå korrelasjonen mellom PID om effektiviteten til ulike industrielle prosesser. Her fokuserer vi bare på å gi en kort gjennomgang av effektiviteten og anvendelsen av PID -kontrollen. Denne artikkelen er utviklet ved å gi en kort introduksjon til kontrollsystemer og relaterte terminologier, i tillegg til motivasjonene for prosjektet. Eksperimentering og observasjoner er gjort, fordeler og ulemper beskrevet med slutt på fremtidige forbedringer. En modell for selvbalanserende robot ble utviklet for å forstå effektiviteten til PID i kontrollsystemet. Gjennom noen strenge tester og eksperimenter ble fordelene og ulempene ved PID -kontrollsystemet oppdaget. Det ble funnet at til tross for mange fordeler med PID -kontroll over tidligere metoder, krever dette systemet fortsatt mange forbedringer. Det er håpet at leseren får en god forståelse av viktigheten av selvbalansering, effektiviteten og manglene ved PID -kontroll

Trinn 1: Introduksjon

Med ankomsten av datamaskiner og industrialisering av prosesser, gjennom menneskets historie, har det alltid vært forskning for å utvikle måter å finjustere prosesser og enda viktigere, å kontrollere dem ved å bruke maskiner autonomt. Hensikten er å redusere menneskets engasjement i disse prosessene, og derved redusere feilen i disse prosessene. Derfor ble feltet "Control System Engineering" utviklet. Kontrollsystemteknikk kan defineres som å bruke forskjellige metoder for å kontrollere driften av en prosess eller vedlikehold av et konstant og foretrukket miljø, det være seg manuelt eller automatisk.

Et enkelt eksempel kan være å kontrollere temperaturen i et rom. Manuell kontroll betyr tilstedeværelsen av en person på et sted som sjekker de nåværende forholdene (sensoren), sammenligner den med ønsket verdi (behandling) og iverksetter passende tiltak for å oppnå ønsket verdi (aktuator). Problemet med denne metoden er at den ikke er veldig pålitelig ettersom en person er utsatt for feil eller uaktsomhet i arbeidet sitt. Et annet problem er også at hastigheten på prosessen som startes av aktuatoren ikke alltid er ensartet, noe som betyr at den noen ganger kan forekomme raskere enn nødvendig, eller noen ganger kan den være treg. Løsningen på dette problemet var å bruke en mikrokontroller for å kontrollere systemet. Mikrokontrolleren er

programmert til å kontrollere prosessen, i henhold til gitte spesifikasjoner, koblet til en krets (skal diskuteres senere), matet ønsket verdi eller betingelser og kontrollerer derved prosessen for å opprettholde ønsket verdi. Fordelen med denne prosessen er at ingen menneskelig intervensjon er nødvendig i denne prosessen. Prosesshastigheten er også jevn

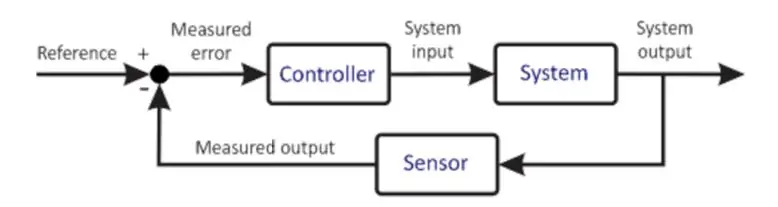
Grunnleggende kontrollsystem

Det forrige diagrammet viser en veldig forenklet versjon av et kontrollsystem. Mikrokontrolleren er kjernen i ethvert kontrollsystem. Det er en veldig viktig komponent, derfor bør valg av valg gjøres nøye basert på kravene til systemet. Mikrokontrolleren mottar et input fra brukeren. Denne inngangen definerer ønsket tilstand for systemet. Mikrokontrolleren mottar også en tilbakemelding fra sensoren. Denne sensoren er koblet til systemets utgang, hvis informasjon sendes tilbake til inngangen. Mikroprosessoren, basert på sin programmering, utfører forskjellige beregninger og gir en utgang til aktuatoren. Aktuatoren, basert på utgangen, styrer anlegget for å prøve å opprettholde disse forholdene. Et eksempel kan være en motordriver som kjører en motor der motorføreren er aktuatoren og motoren er anlegget. Motoren roterer dermed med en gitt hastighet. Sensoren som er tilkoblet leser tilstanden til anlegget for øyeblikket og sender det tilbake til mikrokontrolleren. Mikrokontrolleren sammenligner igjen, gjør beregninger og dermed gjentar syklusen seg selv. Denne prosessen er repeterende og endeløs, hvorved mikrokontrolleren opprettholder de ønskede forholdene

Trinn 2: PID -basert kontrollsystem

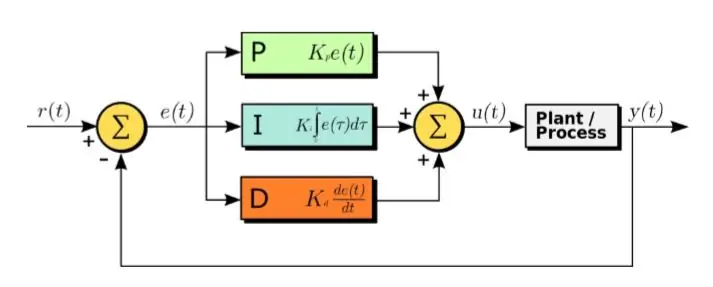
PID -algoritmen er en effektiv metode for å designe et kontrollsystem.

Definisjon

PID står for Proportional, Integral and Derivative. I denne algoritmen er feilsignalet mottatt inngangen. Og følgende ligning brukes på feilsignalet

U (t) = Kp ∗ e (t) + Kd ∗ d/dt (e (t)) + Ki ∗ integral (e (t)) (1.1)

Kort forklaring

Som det kan sees i ligningen ovenfor, blir integralet og derivatet av feilsignalene beregnet, multiplisert med sine respektive konstanter og lagt til sammen med konstanten Kp multiplisert med e (t). Utgangen mates deretter til aktuatoren som får systemet til å kjøre. La oss nå se på hver del av funksjonen etter tur. Denne funksjonen påvirker direkte stigningstid, falltid, topp over skyte, oppgjørstid og steady state -feil.

• Proporsjonal del: Den proporsjonale delen reduserer stigningstiden og reduserer steady state -feilen. Dette betyr at systemet vil ta mindre tid å nå sin høyeste verdi, og når den når sin steady state, vil steady state -feilen være lav. Det øker imidlertid toppoverskridelsen.

• Avledet del: Den avledede delen reduserer overskridelsen og avregningstiden. Dette betyr at systemets forbigående tilstand blir mer dempet. Systemet vil også nå sin stabile tilstand på kortere tid. Det har imidlertid ingen effekt på stigningstiden eller steady state -feilen.

• Integrert del: Den integrerte delen reduserer stigningstiden og eliminerer helt steady state -feilen. Det øker imidlertid toppoverskridelsen og bosettingstiden.

• Tuning: Et godt kontrollsystem vil ha lav stigningstid, avregningstid, toppoverskridelse og steady state -feil. Derfor må Kp, Kd, Ki finjusteres for å justere bidraget fra faktorene ovenfor for å skaffe et godt kontrollsystem.

Figur er vedlagt som viser effekten av å endre forskjellige parametere i PID -algoritmen.

Trinn 3: Selvbalanserende robot

En selvbalanserende robot er en to-lags robot med flere lag.

Roboten vil prøve å balansere seg selv ved bruk av ulik kraft (er). Den vil balansere seg selv ved å bruke makt som motsetter seg resultatet av kreftene på roboten.

Metoder for selvbalansering

Det er fire metoder for selvbalansering av roboter. Disse er som følger:

Selvbalansering ved hjelp av to IR -tilt sensor

Dette er en av de råeste måtene å balansere roboten på, ettersom den krever svært mindre maskinvare og en relativt enkel algoritme. I denne tilnærmingen brukes to vippede IR -sensorer for å måle avstanden mellom bakken og roboten. Basert på avstanden som er beregnet, kan PID brukes til å drive motorene for å balansere roboten tilsvarende. En ulempe med denne metoden er at IR -sensoren kan gå glipp av noen avlesninger. Et annet problem er at en avbrudd og sløyfer er nødvendig for beregning av avstand som øker tidskompleksiteten til algoritmen. Derfor er denne metoden for å balansere roboten ikke særlig effektiv.

Selvbalansering ved hjelp av akselerometer

Akselerometer gir oss akselerasjonen til kroppen i 3 akser. Akselerasjon orientert i y-aksen (oppover) og x-aksen (fremover) gir oss målet for å beregne tyngdekraften og dermed beregne hellingsvinkelen. Vinkelen beregnes som følger:

θ = arctan (Ay/Ax) (1.2)

Ulempen med å bruke denne metoden er at under bevegelsen av roboten vil den horisontale akselerasjonen også bli lagt til avlesningene som er en høyfrekvent støy. Derfor vil helningsvinkelen være unøyaktig.

Selvbalansering ved hjelp av gyroskop

Et gyroskop brukes til å beregne vinkelhastighetene langs de tre aksene. Hellingsvinkelen oppnås ved å bruke følgende ligning.

θp (i) = θp (i − 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1.3)

En stor ulempe med å bruke gyroskopet er at det har en liten DC Bias som er en lavfrekvent støy, og på få tid er de returnerte verdiene helt feil. Dette, etter integrering, vil føre til at nullpunktet driver bort. Som et resultat av det vil roboten forbli i sin vertikale posisjon en stund og vil velte når driften kommer.

Selvbalansering ved hjelp av både akselerometer og gyroskop

Som diskutert ovenfor vil ikke bare bruk av akselerometer eller gyroskop gi oss riktig hellingsvinkel. For å gjøre rede for det, brukes både akselerometer og gyroskop. Disse er begge innebygd i MPU6050. I dette henter vi dataene fra dem begge og smelter dem deretter enten ved å bruke Kalman -filter eller komplementært filter.

• Kalman -filter: Kalman -filteret beregner det beste estimatet av tilstanden til et dynamisk system fra støyende målinger, og minimerer gjennomsnittlig kvadratfeil i estimatet. Den opererer i to stadier, prediksjon og korreksjon, gitt de diskrete stokastiske ligningene som beskriver systemdynamikken. Imidlertid er det en veldig kompleks algoritme å implementere spesielt på en begrenset maskinvare til en mikrokontroller.

• Komplementær filter: Denne algoritmen bruker først og fremst dataene hentet fra gyroskopet og integrerer det over tid for å få hellingsvinkelen. Den bruker også en liten andel av akselerometeravlesninger. Komplementærfilter minimerer faktisk høyfrekvent støy fra akselerometer og lavfrekvent støy fra gyroskopet og smelter dem deretter for å gi den beste nøyaktige helningsvinkelen.

Trinn 4: Design av robot

Vi har designet en selvbalanserende robot ved hjelp av proporsjonal derivatkontroll implementert av komplementærfilter for MPU6050. Denne lille modellen av selvbalanserende robot vil illustrere oss nytten av kontrollsystemer i selvbalansering av roboter.

Systemimplementering:

Systemet er en selvbalanserende robot. Den implementeres ved hjelp av PID -kontrolleren, som er en proporsjonal integrert derivatkontroller. Vi balanserer roboten ved å kjøre hjulene i fallretningen. Ved å gjøre det prøver vi å holde robotens tyngdepunkt over svingpunktet. For å drive hjulene i fallretningen, bør vi vite hvor roboten faller og hastigheten den faller med. Disse dataene innhentes ved bruk av MPU6050 som har et akselerometer og et gyroskop. MPU6050 måler hellingsvinkelen og gir sin effekt til mikrokontrolleren. MPU6050 er koblet til STM -kortet gjennom I2C. I I2C er en ledning for klokken som heter SCL. Den andre er for dataoverføring som er SDA. I dette brukes master slave kommunikasjon. Startadresse og sluttadresse er spesifisert for å vite hvor dataene starter og hvor de slutter. Vi har implementert komplementærfilteret her for MPU6050, som er et mattefilter for å slå sammen utgangene til akselerometer og gyroskop. Etter å ha fått dataene fra MPU6050, vil mikrokontrolleren utføre beregninger for å vite hvor den faller. Basert på beregningene vil STM mikrokontroller gi kommandoer til motorføreren for å kjøre kjøretøyene i fallretning som vil balansere roboten.

Trinn 5: Prosjektkomponenter

Følgende komponenter ble brukt i selvbalanserende robotprosjekt:

STM32F407

En mikrokontroller designet av ST Microelectronics. Det fungerer på ARM Cortex-M Architecture.

Motordriver L298N

Denne IC brukes til å kjøre motoren. Den får to eksterne innganger. En fra mikrokontrolleren som gir den et PWM -signal. Ved å justere bredden på pulsen kan motorhastigheten justeres. Den andre inngangen er spenningskilden som kreves for å drive motoren, som er et 12V batteri i vårt tilfelle.

Likestrømsmotor

En likestrømsmotor går på en likestrømforsyning. I dette eksperimentet kjører likestrømsmotoren ved hjelp av optokoblerne som er koblet til motordriveren. For å drive motoren har vi brukt Motor Drive L298N.

MPU6050

MPU6050 brukes til å få informasjon om hvor roboten faller. Den måler hellingsvinkelen i forhold til nullpunktet som er posisjonen til MPU6050 når programmet begynner å kjøre.

MPU6050 har et 3-akset akselerometer og et 3-akset gyroskop. Akselerometeret måler akselerasjon langs de tre aksene og gyroskopet måler vinkelfrekvens rundt de tre aksene. For å kombinere utgangen må vi filtrere ut lyden fra begge. For å fikse lydene har vi Kalman og komplementærfilter. Vi har implementert komplementærfilter i prosjektet vårt.

Opto Couple 4N35

En optokobler er en enhet som brukes til å isolere lavspenningsdelen og høyspenningsdelen av kretsen. Som navnet antyder, fungerer det på grunnlag av lys. Når lavspenningsdelen får et signal, strømmer det strøm i høyspenningsdelen

Trinn 6: Robotens struktur

Strukturen til roboten forklares som følger:

Fysisk struktur

Den selvbalanserende roboten består av to lag som består av gjennomsiktig plastglass. Detaljene i to lag er gitt nedenfor:

Første lag

I den nederste delen av det første laget har vi plassert en celle for å drive STM -kortet. Det er også plassert to motorer på 4 volt på hver side med dekk tilkoblet for roboten å bevege seg. I den øvre delen av første lag er det plassert to batterier på 4 volt hver (8 volt totalt) og motordriver IC (L298N) for drift av motorer.

Andre lag

I det øvre laget av roboten har vi plassert STM Board på Perf Board. Et annet perf -bord med 4 optokoblere er plassert på topplaget. Gyroskop er også plassert på det øverste laget av roboten fra undersiden. Begge komponentene er plassert i den midterste delen slik at tyngdepunktet holdes så lavt som mulig.

Robotens tyngdepunkt

Tyngdepunktet holdes så lavt som mulig. For dette formålet har vi plassert tunge batterier på bunnlaget og lette komponenter som STM -kort og optokoblere på det øvre laget.

Trinn 7: Kode

Koden ble samlet på Atollic TrueStudio. STM studio ble brukt til feilsøkingsformål.

Trinn 8: Konklusjon

Etter mye eksperimentering og observasjon kommer vi endelig til det punktet hvor vi oppsummerer resultatene våre og diskuterer hvor langt vi lyktes med å implementere og utarbeide systemets effektivitet.

Generell gjennomgang

Under eksperimenteringen ble motorens hastighet vellykket kontrollert ved bruk av PID -algoritmen. Kurven er imidlertid ikke akkurat en jevn rett linje. Det er mange grunner til det:

• Sensoren, selv om den er koblet til et lavpassfilter, gir fremdeles visse endelige nedstigninger; disse skyldes de ikke -lineære motstandene og noen uunngåelige årsaker til den analoge elektronikken.

• Motoren roterer ikke jevnt under liten spenning eller PWM. Det gir ryk som kan forårsake feil verdier som mates til systemet.

• På grunn av vingling kan sensoren gå glipp av noen slisser som gir høyere verdier. • En annen stor årsak til feil kan være kjerneklokkefrekvensen til STM -mikrokontrolleren. Denne modellen av STM mikrokontroller gir en kjerneklokke på 168MHz. Selv om dette problemet ble behandlet i dette prosjektet, er det en generell oppfatning om denne modellen at den ikke akkurat gir så høy frekvens.

Den åpne sløyfehastigheten gir en veldig jevn linje med bare noen få uventede verdier. PID -algoritmen fungerer også fint som gir en meget lav avregningstid for motoren. Motorens PID -algoritme ble testet under forskjellige spenninger som holdt referansehastigheten konstant. Spenningsendringen endrer ikke motorens turtall og viser at PID -algoritmen fungerer fint

Effektivitet

Her diskuterer vi effektiviteten til PID -kontrolleren som vi observerte under eksperimentet.

Enkel implementering

Vi har sett i delen eksperimentering og observasjoner at en PID -kontroller er veldig enkel å implementere. Det krever bare tre parametere eller konstanter som må stilles inn for å ha et hastighetskontrollsystem

Uovertruffen effektivitet for lineære systemer

Lineær PID -kontroller er den mest effektive i familien av kontrollere fordi logikken er veldig enkel og applikasjonen er utbredt ved lineære eller ganske lineære applikasjoner.

Begrensninger

Vi forklarte abstrakt om begrensningene i dette systemet. Her diskuterer vi noen av dem som vi observerte.

Valg av konstanter

Vi har sett at selv om en PID -kontroller er enkel å implementere, er det likevel en stor ulempe med systemet at trinnet med å velge verdien av konstanter er en møysommelig. som man må gjøre vanskelige beregninger. Den andre måten er hit and trial -metoden, men det er heller ikke effektivt.

Konstanter er ikke alltid konstante

De eksperimentelle resultatene viste at for forskjellige verdier av referansehastigheten for motoren, fungerte PID -kontrolleren feil med de samme verdiene for PID -konstantene. For forskjellige hastigheter måtte konstantene velges forskjellig, og dette øker beregningskostnaden eksponensielt.

Ikke lineær

PID -kontrolleren som brukes i vårt tilfelle er lineær, derfor kan den bare brukes på lineære systemer. For ikke-lineære systemer må kontrolleren implementeres forskjellig. Selv om forskjellige ikke -lineære metoder for PID er tilgjengelige, krever det at flere parametere velges. Dette igjen gjør systemet uønsket på grunn av høye beregningskostnader.

Første trykk påkrevd

Vi viste i eksperimenteringsdelen at for en ganske liten referansehastighet der feilen er ganske liten i starten, er PWM levert av PID så liten at den ikke genererer det nødvendige startmomentet for motoren. Så motoren i noen forsøk går ikke, eller i andre forsøk gir en stor overskridelse og lengre avviklingstid.

Trinn 9: Spesiell takk

Spesiell takk til gruppemedlemmene mine som hjalp meg gjennom dette prosjektet.

Jeg vil laste opp lenken til videoen snart.

Jeg håper du synes dette er interessant.

Dette er Tahir Ul Haq fra UET som melder seg ut. Jubel !!!