Måling av temperatur fra PT100 ved bruk av Arduino: 6 trinn (med bilder)

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-31 10:23

PT100 er en motstandstemperaturdetektor (RTD) som endrer motstanden avhengig av omgivelsestemperaturen, den brukes mye til industrielle prosesser med langsom dynamikk og relativt brede temperaturområder. Den brukes til langsomme dynamiske prosesser fordi RTD har treg responstid (som jeg snakker mer om senere), men er nøyaktige og har lav drift over tid. Det jeg skal vise deg i denne Instructable ville ikke være opp til industriell standard, men det vil utsette deg for en alternativ måte å måle temperatur på enn å bruke LM35 som mange hobbyfolk ville være kjent med og kretsteorien vist kan brukes på andre sensorer.

Trinn 1: Komponenter

1x PT100 (to ledninger)

1x Arduino (hvilken som helst modell)

3x 741 driftsforsterkere (LM741 eller UA741)

1x 80ohm motstand

2x 3,9 kohms motstander

2 x 3,3 kOhm motstander

2x 8,2 kOhm motstander

2x 47kohms motstander

1x 5kohms potensiometer

1x to terminal strømforsyning eller 8x 1,5V AA batterier

Jeg bruker en to -leders PT100, tre og fire -leders PT100 vil ha forskjellige kretser. Motstandsverdiene for de fleste av disse trenger ikke å være nøyaktig de samme som ovenfor, men hvis det er et par motstander, dvs. 3,9Kohms, hvis du byttet dem for la oss si 5k, må du bytte begge for 5k som da må være det samme. Når vi får kretsen vil jeg si effekten av å velge forskjellige verdier. For operasjonsforsterkere (op -forsterkere) kan du bruke andre op -forsterkere, men det er disse jeg brukte.

Trinn 2: Wheatstone Bridge

Jeg må først snakke om formelen for å få temperaturen fra motstanden for PT100 før jeg snakker om den første delen av kretsen, formelen for motstanden er som følger:

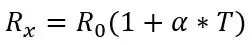
hvor Rx er PT100 -motstanden, R0 er PT100 -motstanden ved 0 grader C, α er temperaturmotstandskoeffisienten og T er temperaturen.

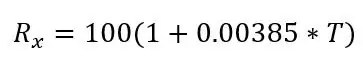
R0 er 100ohms da dette er en PT100, hvis det var en PT1000, ville R0 være 1000ohms. α er 0,00385 ohm/grader C hentet fra databladet. Det er også en mer nøyaktig formel som finnes her, men formelen ovenfor vil gjøre for dette prosjektet. Hvis vi transponerer formelen, kan vi beregne temperaturen for en gitt motstand:

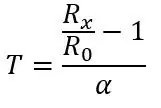
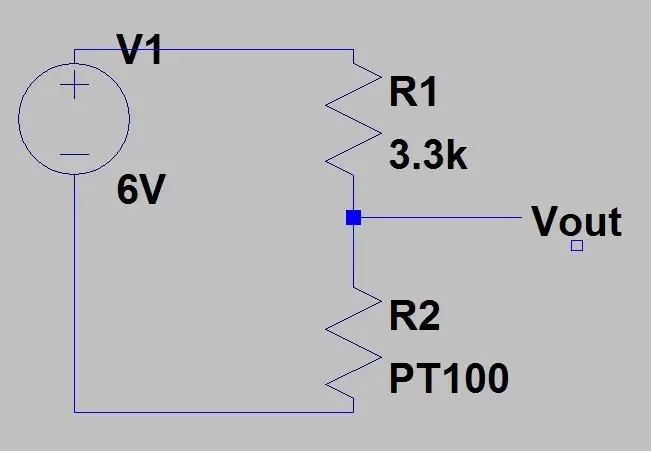
La oss si at vi vil måle noe som ville ha et temperaturområde på -51,85 til 130 grader C, og vi plasserte PT100 i kretsen vist på bilde 1. Ved å bruke ligningen ovenfor og ligningen for spenningen ut av en spenningsdeler (vist i det første bildet) kan vi beregne spenningsområdet. Bunnen av området T = -51,85 (80 ohm)

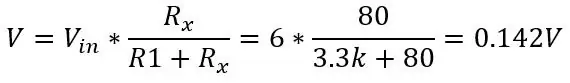
og ved 130 grader (150 ohm):

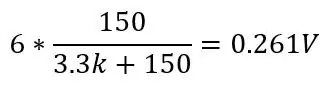
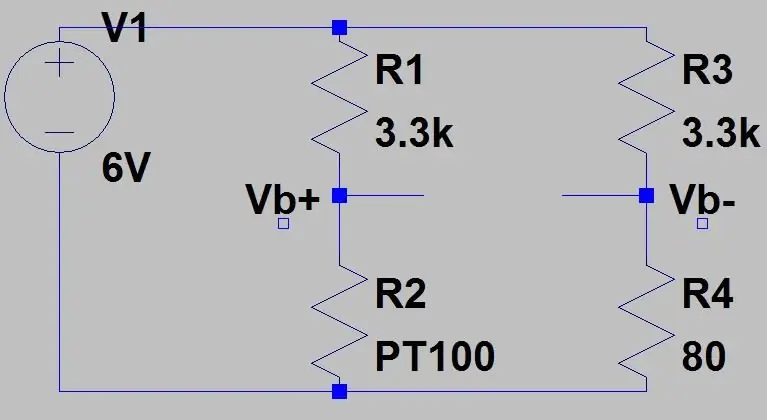
Dette vil gi et område på 0.1187V og en DC -forskyvning på 0.142 fordi vi vet at temperaturen vår aldri vil komme under -51.85 grader C, dette vil redusere følsomheten i området vi bryr oss om (80 til 130 ohm) når vi forsterker denne spenningen. For å bli kvitt denne DC -forskyvningen og øke vår følsomhet kan vi bruke en Wheatstone -bro som er vist på det andre bildet.

Utgangen til den andre spenningsdeleren (Vb-) blir trukket fra den første spenningsdelerutgangen (Vb+) ved hjelp av en differensialforsterker senere. Formelen for utgangen til broen er bare to spenningsdelere:

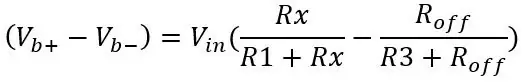
Spenningen ut for PT100 er 80 ohm og bruker de andre verdiene på bildet:

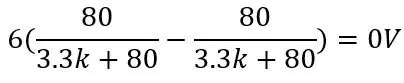
og for Pt100 som er 150 ohm:

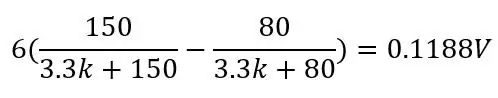
Ved å bruke Wheatstone blir vi kvitt DC -forskyvningen og øker følsomheten etter forsterkning. Nå som vi vet hvordan Wheatstone -broen fungerer, kan vi snakke om hvorfor vi bruker 80ohms og 3.3kohms. 80ohms er litt forklart fra formelen ovenfor, velg denne verdien (vi kaller dette offset -motstanden Roff) for å være det nederste området for temperaturen din eller enda bedre, litt under bunnen av området ditt, hvis dette brukes til et kontrollsystem for temperaturregulering eller noe sånt, vil du vite hvor lav temperaturen kommer under temperaturområdet ditt. Så hvis -51,85C er bunnen av området ditt, bruk 74,975 ohm (-65 grader C) for din Roff.

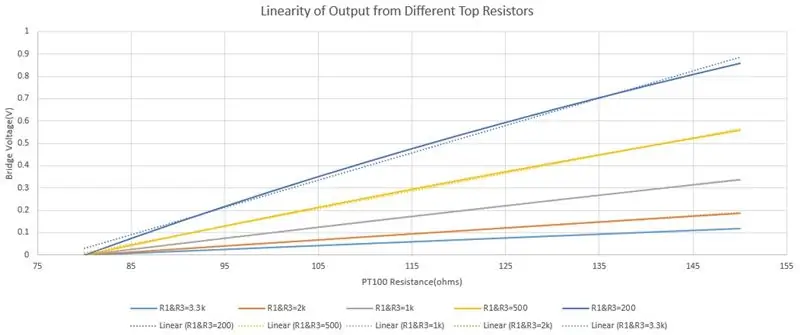
Jeg valgte 3,3k for R1 og R3 av to grunner, for å begrense strømmen og øke lineariteten til utgangen. Ettersom PT100 endrer motstand på grunn av temperatur, vil for mye strøm passere gjennom det gi feil avlesning på grunn av selvoppvarming, så jeg valgte en maksimal strøm på 5-10mA. Når PT100 er 80ohms er strømmen 1.775mA så trygt under maksimalområdet. Du reduserer motstanden for å øke følsomheten, men dette kan ha en negativ effekt på lineariteten, ettersom vi vil bruke ligningen til en linje senere (y = mx+c) som har en ikke-lineær utgang, vil innføre feil. Det tredje bildet har en graf over broutgangen ved bruk av forskjellige toppmotstander, den heltrukne linjen er den faktiske utgangen og den stiplede linjen er den lineære tilnærmingen. Du kan se i den mørkeblå grafen (R1 & R3 = 200ohms) gir det største spenningsområdet, men utgangen er minst lineær. Den lyseblå (R1 & R3 = 3,3 kohms) gir det minste spenningsområdet, men den stiplede linjen og den heltrukne linjen overlapper hverandre og viser at linjæriteten er veldig god.

Du er velkommen til å endre disse verdiene slik at de passer til søknaden din, også hvis du endrer spenningen, må du passe på at strømmen ikke blir for høy.

Trinn 3: Forsterkning

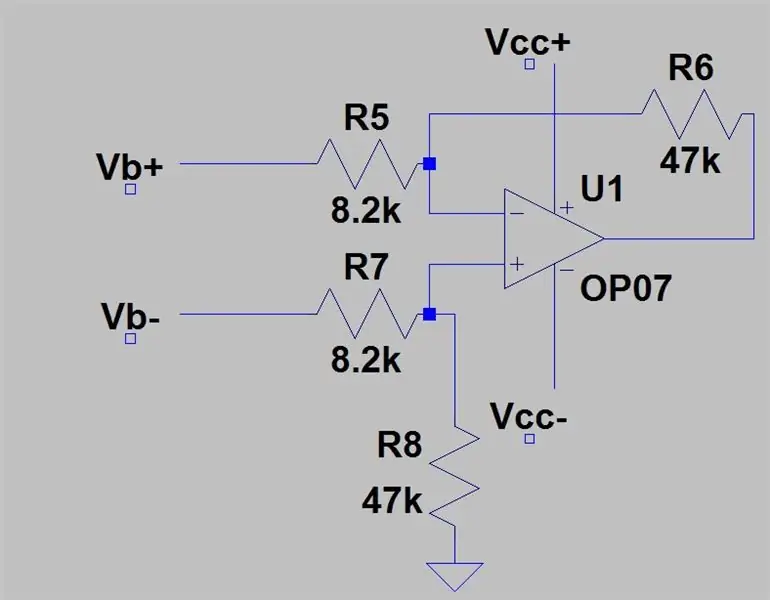
I det siste trinnet fant vi utgangsområdet for de to spenningsdelerne som var trukket fra 0 til 0,11187, men vi har ikke snakket om hvordan vi trekker disse spenningene. For å gjøre dette trenger vi en differensialforsterker som trekker den ene inngangen fra den andre og forsterker dette med forsterkningen til forsterkeren. Kretsen for en differensialforsterker er vist på det første bildet. Du mater Vb+ til den inverterende inngangen og Vb- i den ikke-inverterende inngangen, og utgangen vil være Vb+- Vb- med en forsterkning på en dvs. ingen forsterkning, men ved å legge til motstandene vist på bildet legger vi til en forsterkning på 5,731. Gevinsten er gitt av:

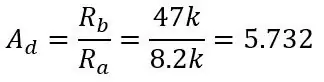
Ra er R5 & R7 og Rb er R6 & R8, spenningen ut er gitt av:

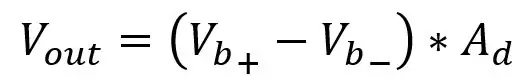
Det er to problemer med å bare koble denne forsterkeren til broens utgang, lasteeffekten og endre gevinsten. Hvis du endrer forsterkningen til forsterkeren, må du bytte minst to motstander ettersom de to motstandsparene må være like, så å ha to gryter som må ha samme verdi ville være irriterende, så vi bruker noe som kalles en instrumenteringsforsterker som jeg snakker om nedenfor. Lasteffekten er inngangsmotstandene i forsterkeren som påvirker spenningsfallet over PT100, vi vil at spenningen over PT100 skal være uendret, og for å gjøre dette kan vi velge veldig store motstander for inngangsmotstandene slik at parallellmotstanden til PT100 og inngangsmotstanden er veldig nær PT100 -motstanden, men dette kan forårsake problemer med støy og spenningsutgang som jeg ikke kommer til å gå inn på. Bare velg mellomtone i Kohms -området, men som jeg sa, å ha små motstander er også dårlig, så vi endrer kretsen litt.

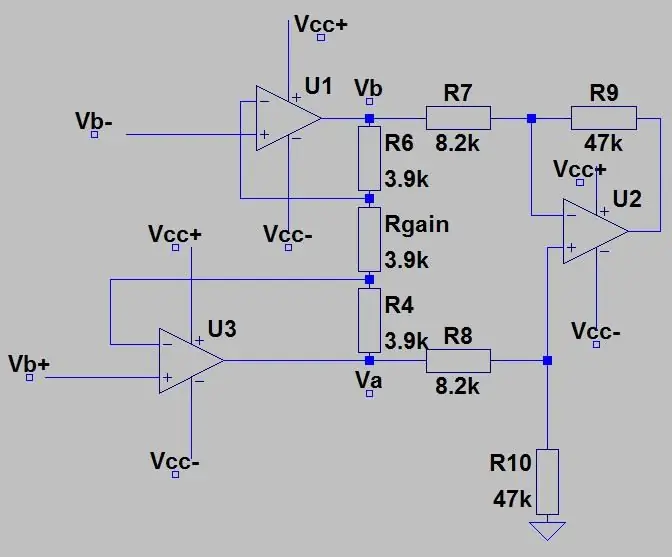
På det andre bildet har vi utgangen fra broen koblet til en instrumenteringsforsterker som fungerer som en bufferforsterker for å skille de to halvdelene av kretsene (broen og forsterkningen), og gjør det også mulig å forsterke inngangen ved å endre bare ett potensiometer (Rgain). Gevinsten til instrumenteringsforsterkeren er gitt av:

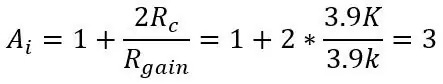
hvor Rc er de to 3,9k motstandene over og under potten.

Ved å redusere Rgain øker forsterkningen. Så på punkt Va og Vb (forsterket Vb+ og Vb-) er det bare en differensialforsterker som før, og den totale gevinsten til kretsen er bare gevinstene multiplisert sammen.

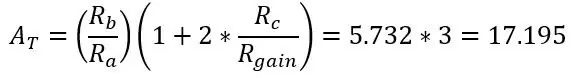
For å velge din gevinst, vil du gjøre noe som vi gjorde før med Roff. Fordi vi bruker Arduino som har en 5V adc, bør maksimal utgang fra kretsen 5V ved maks temperatur du valgte. La oss velge 150 ohm som maksimal motstand, og brospenningen som ikke er forsterket var 0,11187V, forsterkningen vi trenger er 42,185 (5/0,1187)

La oss si at vi beholder Ra, Rb og Rc som 8,2k, 47k og 3,9k, vi trenger bare å finne verdien for potten Rgain:

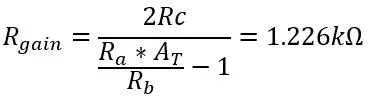
Så for å få hele 5 volt ut av temperaturområdet vi bruker, endre verdien av Rgain til 1,226k. Utgangsspenningen som kommer ut av differensialforsterkeren er gitt av:

Trinn 4: Slå på kretsen

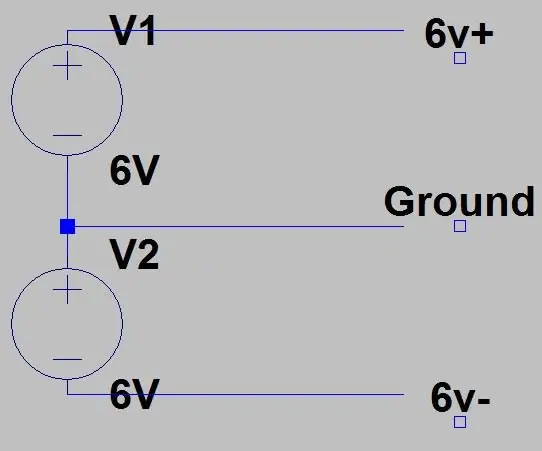
Dette er det siste trinnet i kretsen, du har kanskje lagt merke til Vcc+ og Vcc- på op amp kretsene, dette er fordi de trenger både positiv og negativ spenning for å fungere skikkelig, du kan få enkeltskinne op-ampere, men jeg bestemte meg å bruke denne forsterkeren som det var det jeg hadde liggende. Så vi leverer +6V og -6V, det er tre måter vi kan gjøre dette på. Den første er vist i det første bildet der vi må to strømforsyninger eller to utgangsterminaler fra en enkelt strømforsyning, ha begge på 6V og ha en positiv utgang koblet til den andre av den andre. 6V for topptilførselen vil være vår +6V, positiv for bunnforsyningen er GND og minus for bunnforsyningen er -6V. KOBLER KUN DEN SOM HVIS GND -ene til de to forsyningene er atskilt eller det vil skade strømforsyningen. Alle kommersielle strømforsyninger ville ha skilt GND -er, men hvis du vil sjekke, bruk kontinuitetstester på multimeteret ditt, hvis det summer, ikke bruk dette oppsettet og bruk det neste. På min hjemmelagde forsyning sprengte jeg sikringen med dette.

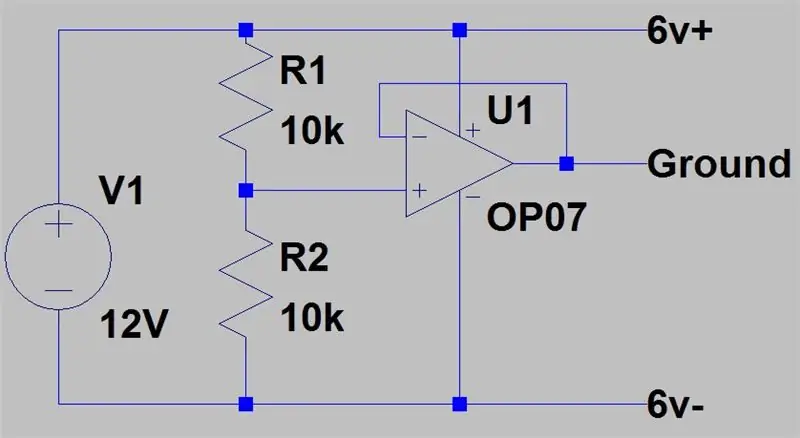
På det andre bildet er det andre oppsettet vi kan ha, det krever en forsyning for å ha dobbel spenning fra den andre, men vil ikke skade forsyningen hvis GND -ene er tilkoblet. Vi har to forsyninger, en på 12V og en annen på 6V. 12V vil fungere som vår +6V, 6V ut av den andre forsyningen vil fungere som GND og de to faktiske GNDene ut av forsyningene vil fungere som -6V.

Dette siste oppsettet er for strømforsyningene med bare en utgang, det bruker en bufferforsterker med forsterkning 1 for å skape en virtuell bakken ved å føre halvparten av forsyningsspenningen gjennom bufferforsterkeren. Da vil 12V fungere som +6V og den faktiske GND -terminalen vil være -6V.

Hvis du vil bruke batterier, vil jeg foreslå det første oppsettet, men et problem med batterier er at spenningen vil falle når de begynner å dø, og spenningen ut av broen vil også falle, noe som gir feil temperaturavlesninger. Du kan selvfølgelig lese spenningen fra batteriene og inkludere dem i beregningene eller bruke regulatorer og flere batterier. Til slutt er det opp til deg.

Trinn 5: Full krets og kode

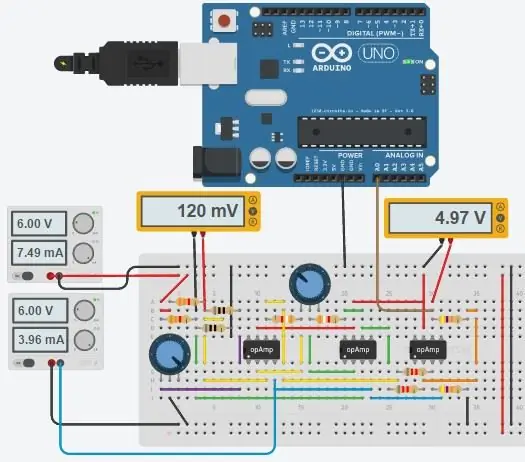
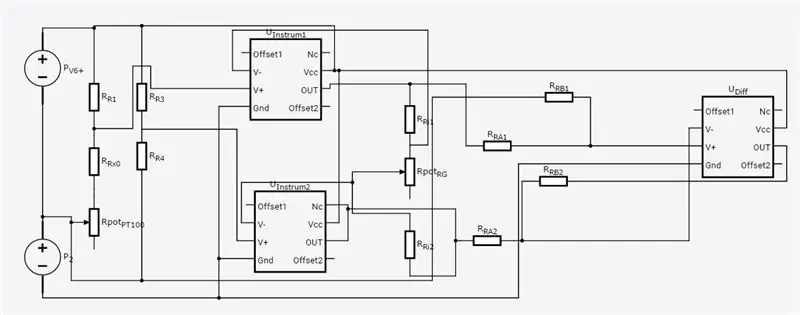
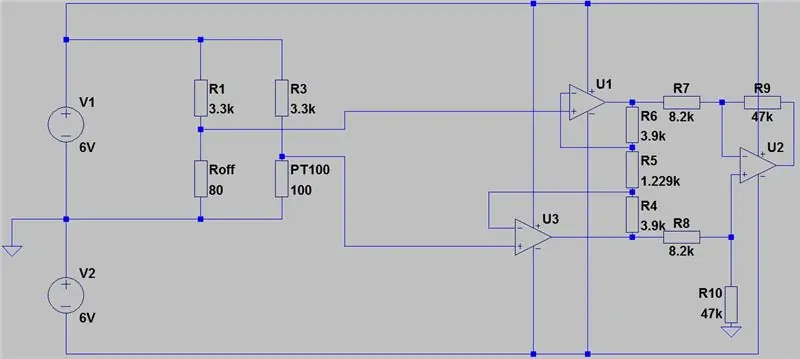
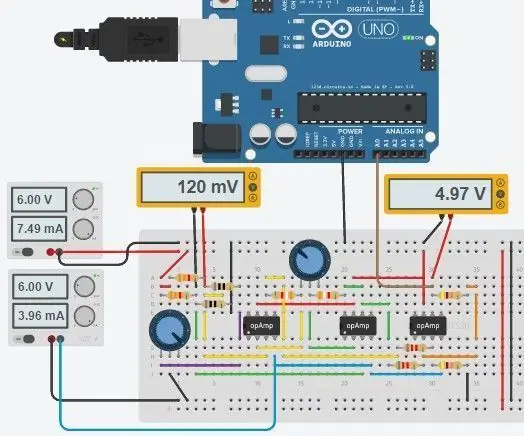
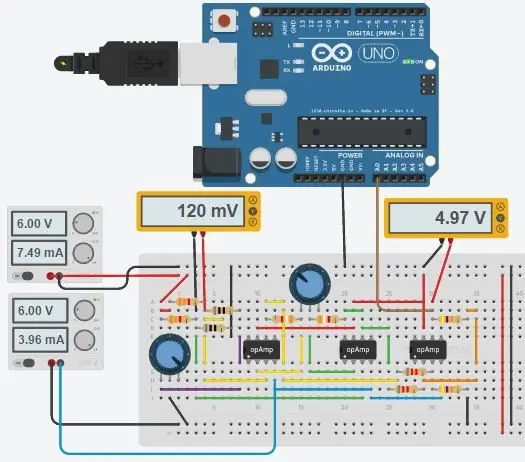
Hele kretsen er vist ovenfor, og den ble laget i Autodesks nye Circuits.io som lar deg lage kretser på brødbrett, redigere kretsdiagram (vist på bilde 2) og PCB -diagrammer og den beste delen, lar deg simulere kretsen fra brødbrettet og kan til og med programmere en Arduino og koble den til i breadboard -modusen, lenger ned på siden er simuleringen, og du kan leke med to potter. Hvis du vil kopiere kretsen og sette inn dine egne verdier, kan du finne kretsen her. Den første potten er 70ohms og i serie med en 80ohm motstand som simulerer PT100 med en rekkevidde på 80-150ohms, den andre potten er gevinsten til instrumenteringsforsterkeren. Dessverre brukte jeg et bibliotek jeg lastet ned for koden min, så Arduino er ikke inkludert i kretsen nedenfor, men det er bare to ekstra ledninger du trenger å koble til. Hvis du er mer komfortabel med LTspice, inkluderte jeg en asc -fil med kretsen.

Koble A0 -pinnen til utgangen på differensialforsterkeren

Koble GND for Arduino til kretsens GND (IKKE -6V)

Og det er kretsen gjort, nå til koden. Tidligere nevnte jeg at vi skal bruke formelen y = mx+c, nå skal vi beregne m (stigningen) og c (forskyvningen). I Arduino leser vi spenning, men temperaturligningen trenger oss til å kjenne motstanden til PT100, så en måte vi kan gjøre dette på er å erstatte Serial.println (temp) med Serial.println (V) og registrere spenning og motstand ved to temperaturer. Når du gjør denne testen, la PT100 være i fred et øyeblikk, for eksempel et minutt eller to, og hold deg borte fra varmekilder (sollys, bærbar vifte, kroppen din osv.).

Det første punktet vi kan ta er romtemperatur, når du har kretsen tilkoblet og fungerer, registrerer du spenningen (Vt1) som er lest av Arduino på den serielle skjermen og kobler raskt fra PT100 og registrerer motstanden (Rt1), ikke legg din hendene på sonden når du kobler fra, da dette vil endre motstanden. For den andre temperaturen kunne vi plassere sonden i isvann eller varmt vann (vær forsiktig hvis du bruker varmt vann) og gjenta det vi gjorde før vi fant Vt2 og Rt2. Like etter at du har plassert sonden i væsken, vent et minutt eller to til motstanden har lagt seg. Hvis du er interessert i tidsresponsen til PT100, kan du registrere spenningen fra den serielle skjermen hvert 2. sekund, så kan vi tegne en graf fra dette, så skal jeg forklare det senere. Ved å bruke de to spenningene og motstandene kan vi beregne stigningen som følger:

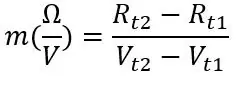
Rt1 og Rt2 er motstandene ved de to temperaturene og det samme gjelder for spenningene Vt1 og Vt2. Fra skråningen og ett av de to settene med punkter du registrerte kan vi beregne forskyvningen:

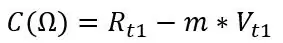
C skal være i nærheten av din virkelige Roff. Fra min simulering beregnet jeg disse verdiene:

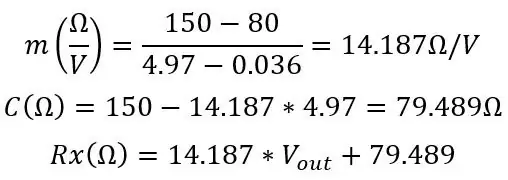
Fra denne motstanden kan vi finne temperaturen vår ved å bruke formelen vi hadde i starten:

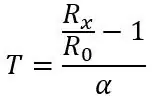
Og det er det, koden for Arduino er nedenfor. Hvis du har problemer, er det bare å legge igjen en kommentar, så skal jeg prøve å hjelpe.

Det er ingen bilder av kretsen jeg lagde slik jeg gjorde den for en stund siden, og jeg har ikke PT100 lenger til å remake og teste, men du må bare tro meg at den fungerer. Det er ikke mye om PT100 på Instructables som jeg fant, så det var derfor jeg gjorde denne ible.

I det neste trinnet skal jeg snakke om tidsresponsen til PT100, og hvis du ikke er interessert i matematikk, når du måler en temperaturendring, la PT100 slå seg til ro i et minutt eller så før du leser.

Hvis du er interessert i å se andre prosjekter jeg har laget, kan du besøke min

Blogg: Roboroblog

YouTube -kanal: Roboro

Eller se på mine andre instrukser: her

Hvis HTML -filen roter med koden nedenfor, er koden vedlagt

* Denne koden beregner temperaturen ved hjelp av en PT100

* Skrevet av Roboro * Github: <a href = "https://github.com/RonanB96/Read-Temp-From-PT100-… <a href =" https://github.com/RonanB96/Read-Temp- From-PT100-… <a href = "https://github.com/RonanB96/Read-Temp-From-PT100-… >>>>>>>>> * Circuit: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Blog: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Instrustable Post: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * */ //You'll need to download this timer library from here //https://www.doctormonk.com/search?q=timer #include "Timer.h" // Define Variables float V; float temp; float Rx; // Variables to convert voltage to resistance float C = 79.489; float slope = 14.187; // Variables to convert resistance to temp float R0 = 100.0; float alpha = 0.00385; int Vin = A0; // Vin is Analog Pin A0 Timer t; // Define Timer object

void setup() {

Serial.begin(9600); // Set Baudrate at 9600 pinMode(Vin, INPUT); // Make Vin Input t.every(100, takeReading); // Take Reading Every 100ms } void loop() { t.update(); // Update Timer } void takeReading(){ // Bits to Voltage V = (analogRead(Vin)/1023.0)*5.0; // (bits/2^n-1)*Vmax // Voltage to resistance Rx = V*slope+C; //y=mx+c // Resistance to Temperature temp= (Rx/R0-1.0)/alpha; // from Rx = R0(1+alpha*X) // Uncommect to convet celsius to fehrenheit // temp = temp*1.8+32; Serial.println(temp); }

Step 6: Time Response of PT100

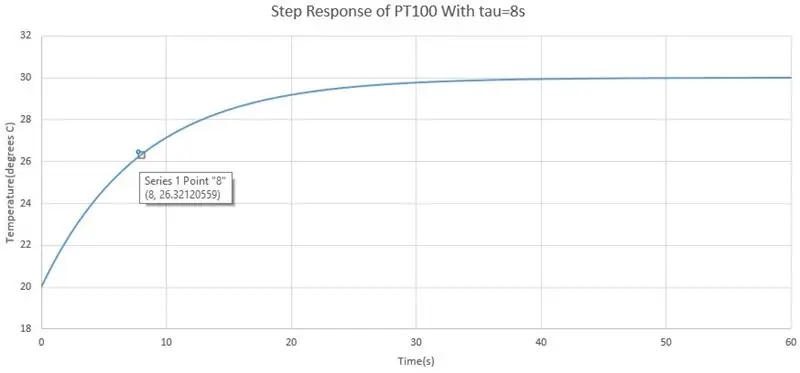
Så jeg nevnte at PT100 har en treg respons, men vi kan når som helst få en formel for gjeldende temperatur lest av PT100. Svaret til PT100 er et førsteordens svar som kan skrives med Laplace -termer, dvs. overføringsfunksjon, som:

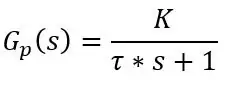
der tau (τ) er tidskonstanten, K er systemets forsterkning og s er Laplace -operatøren som kan skrives som jω hvor ω er frekvens.

Tidskonstanten forteller deg hvor lang tid det tar et førsteordens system å slå seg ned til den nye verdien, og en regel eller tommel er at 5*tau er hvor lang tid det tar å slå seg ned i den nye steady state. Forsterkningen K forteller deg hvor mye inngangen vil bli forsterket. Med PT100 er forsterkningen hvor mye motstanden endres dividert med temperaturendringen, fra å velge to tilfeldige verdier fra dette databladet, fikk jeg en gevinst på 0,3856 ohm/C.

Før jeg sa at du kunne registrere spenningen hvert 2. sekund etter at du satte sonden i væsken, varm eller kald, kan vi beregne systemets tidskonstant fra dette. Først må du identifisere hvor startpunktet og sluttpunktet er. Startpunktet er spenningen før du setter sonden i væsken og sluttpunktet er når den slo seg ned. Deretter trekker du dem, og det er spenningsendringen i trinnet, testen du utførte var en trinnendring som er en plutselig endring i inngang til et system, trinnet er temperatur. Nå på grafen, gå til 63,2% av spenningsendringen, og denne tiden er tidskonstanten.

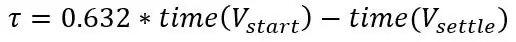
Hvis du kobler denne verdien til overføringsfunksjonen, har du deretter formelen for å beskrive frekvensresponsen til systemene, men det er ikke det vi ønsker akkurat nå, vi vil ha den faktiske temperaturen på tidspunktet t for et trinn i temperaturen, så vi går å måtte utføre en invers Laplace -transformasjon av et trinn inn i systemet. Overføringsfunksjonen til et førsteordens system med inngang av et trinn er som følger:

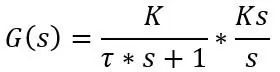
Hvor Ks er trinnstørrelsen, dvs. temperaturforskjellen. Så la oss si at sonden er avgjort ved 20 grader C, plassert i vann ved 30 grader C og sonden har en tidskonstant på 8s, overføringsfunksjonen og tidsdomeneformelen er som følger:

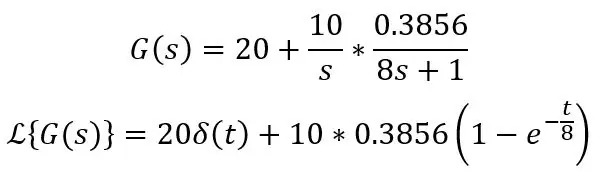
Δ (t) betyr bare en impuls, dvs. DC -forskyvning på 20 grader C i dette tilfellet, du kan bare skrive 20 i ligningene dine når du beregner dette. Dette er standardligningen for trinnet inn i et førsteordens system:

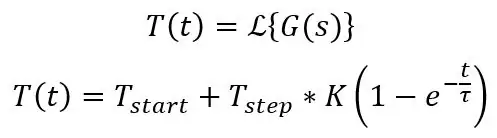
Ovenstående beregner temperaturen på tidspunktet t, men dette vil fungere for spenningen da de er proporsjonale med hverandre, du trenger bare start- og sluttverdien, tidskonstant og trinnstørrelse. Et nettsted som heter Symbolab er flott for å sjekke om matematikken din stemmer, den kan gjøre Laplace, integrasjon, differensiering og mange andre ting, og det gir deg alle trinnene på veien. Den inverse Laplace -transformasjonen ovenfor finner du her.