
Innholdsfortegnelse:
- Forfatter John Day day@howwhatproduce.com.
- Public 2024-01-30 11:23.
- Sist endret 2025-01-23 15:02.



Jeg vet hva du synes: "Huh? Det er mange instrukser om hvordan du bruker mikrokontrollere til å måle signalfrekvens. Gjesp." Men vent, det er en nyhet i denne: Jeg beskriver en metode for måling av frekvenser som er mye høyere enn en mikrokontroller (MCU) kan bære og signalets driftssyklus - alt på samme tid!
Enhetens frekvensområde spenner fra ~ 43 Hz til ~ 450 kHz, mens driftssyklusen varierer fra 1% til 99%.
La meg forklare "kan bære" -delen: en MCU måler perioden for et firkantbølgesignal, T, ved å spore tid mellom to påfølgende overgangshendelser. For eksempel hopper lav til høy spenning på en av I/O-pinnene. Det gjør det ved å telle antall pulser på sin egen interne klokke. Naivt bør den øvre grensen for målte frekvenser følge Nyqvist-Shannon-prøvetakingsteoremet; det vil si omtrent halvparten av MCUs klokkefrekvens. I virkeligheten er grensen mye, mye lavere, fordi MCU må utføre kode for å håndtere avbrudd, lagre variabler, utføre aritmetiske operasjoner, vise resultater, etc. I mine eksperimenter med en 48 MHz MCU var det minimale antallet klokkesykluser mellom målbare overganger ca 106. Derfor vil den øvre grensen for det målbare frekvensområdet i dette tilfellet være 48 000 /212 /2 = 226,4 kHz.
Mens MCU måler signalets periode, kan den også bestemme pulsbredden, P: tiden for signalspenningen forblir høy. Med andre ord, tid mellom lav til høy og høy til lav overgang. Signalets driftssyklus blir deretter definert som følgende prosentandel:
Plikt = 100% * P / T
Akkurat som i tilfellet med frekvens, er det en praktisk grense for pulsbredde. Ved å bruke eksemplet ovenfor ville 106 klokkesykluser begrense pulsbredden til ikke mindre enn 2,21 mikrosekunder. Eller ikke mindre enn 50% ved 226,4 kHz.
En av måtene å øke den øvre frekvensgrensen for firkantbølgesignaler er bruk av digitale skillelinjer som bruker flip-flops. Å dele inngangsfrekvensen med n ville utvide det målbare øvre området n ganger. Dette er gode nyheter, digitale skillere har en grunnleggende feil: delt signal mister informasjonen om pulsbredde (og driftssyklus)! På grunn av måten delerne fungerer på, har produksjonen alltid 50% driftssyklus. Nedtur…
På de følgende sidene vil jeg imidlertid vise hvordan jeg kan dele frekvensen digitalt og bevare den opprinnelige pulsbredden slik at jeg kan måle signaler langt utover grensene som er lagt ved direkte telling.
Trinn 1: Digital Frequency Division
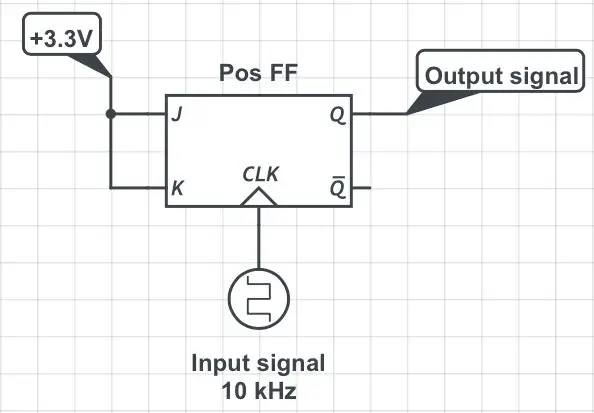
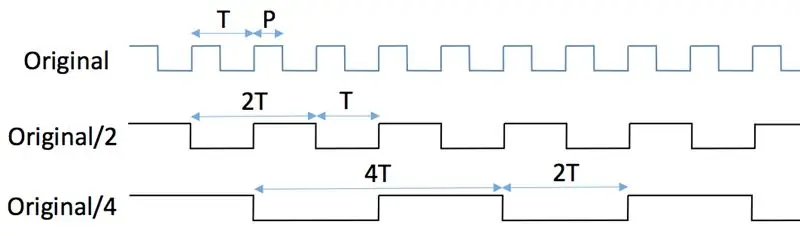
Tradisjonelle digitale frekvensdelere bruker flip-flops; denne opplæringen forklarer pent prinsipper for hvordan man konstruerer skillevegger ved bruk av standard JK flip-flops. Dette løser problemet med inngangsfrekvenser for høye for MCU, men har en stor ulempe: delt signal har 50% driftssyklus uavhengig av inngangssignalets plikt! For å se hvorfor det er tilfelle, se på de to første figurene. Det originale signalet med periode T og pulsbredde P mates inn i klokkestiften på en JK flip-flop mens dens J- og K-pinner til enhver tid holdes høyt (første figur). 3.3V logikk er forutsatt gjennomgående. La oss anta at vippen blir utløst av den positive (dvs. stigende) kanten av klokken. Under disse forholdene skjer det endringer i tilstanden til utgangspinnen (individuelle "flips" og "flops") hver gang klokkestiften går fra lav til høy. Klokkens høye til lave overgang (dvs. den negative kanten) ignoreres fullstendig. Se den andre figuren. Utgangspinnen, Q, sender ut et signal hvis periode er dobbelt så lang som den opprinnelige perioden, dvs. at frekvensen er halvert. Utgangens pulsbredde er alltid lik T. Følgelig går den opprinnelige pulsbredden, P, tapt.
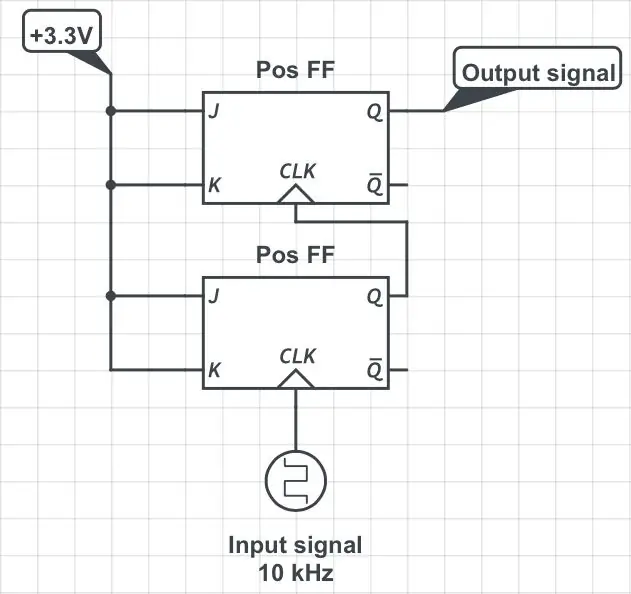
Ved å legge til en annen JK flip-flop i en konfigurasjon vist i den tredje figuren, deler den opprinnelige frekvensen med 4. Hvis du legger til flere flip-flops på samme sekvensielle måte, deler du frekvensen med påfølgende effekter på 2: 8, 16, 32, etc.
Problem: hvordan dele frekvensen til en firkantbølge mens du beholder pulsbredden?
Ideen er å legge til en negativ kantutløst JK-flip-flop på riktig måte til blandingen. La oss kalle det "Neg FF"; se fjerde figur. Her betyr "riktig" at J- og K-pinnene til den nye flip-floppen er knyttet til henholdsvis Q- og Qbar-utgangspinnene i divider-by-4 ("Pos FF") illustrert i forrige figur. (Her er "bar" den horisontale linjen over Q -symbolet som indikerer logisk negasjon.) For å se hva dette oppnår, ta en titt på funksjonstabellen til "Neg FF" i den femte figuren: Negs utgangspinner, Q og Qbar, speiler tilstanden til inngangspinnene, henholdsvis J og K. Hvilket betyr at de speiler tilstanden til Pos 'Q og Qbar. Men Negs flip-flop-handling må vente på den negative kanten av det originale signalet, som kommer på tidspunktet P etter den positive kanten. Aha!
De resulterende bølgeformene er illustrert i den sjette figuren. "Pos Q" -utgangssignal ved 1/4 frekvens, "Pos Qbar" er det invers, "Neg Q" følger "Pos Q" forskjøvet med pulsbredde P, og "Neg Qbar" er invers. Du kan bekrefte at det logiske OG for "Pos Qbar" og "Neg Q" gir et pulstog preget av den opprinnelige pulsbredden P og 1/4 av frekvensen. Bingo!
Først brukte jeg akkurat dette utgangssignalet til å mate MCU. Det viste seg imidlertid å være problematisk for svært korte pulsbredder på grunn av MCUs 106 syklusbegrensning nevnt i introduksjonen. Jeg har løst dette lille problemet ved å velge en annen utgang: "Pos Qbar" OG "Neg Qbar" i stedet. Ett blikk på bølgeformene bør overbevise deg om at pulsbredden til denne bestemte bølgeformen, P ', varierer mellom T og 2T i stedet for (0, T) område for P. P kan enkelt gjenopprettes fra P' ved å:
P = 2T - P '
Trinn 2: Anbefalt maskinvare



Jeg liker virkelig den relative nykommeren til elektroniske hobbyfolk: Atmel SAM D21 MCUer basert på 32-biters ARM Cortex M0+ -prosessoren som opererer med 48 MHz klokkefrekvens, mye høyere enn de eldre Atmels. Til dette prosjektet kjøpte jeg:
- ItsyBitsy M0 Express MCU -brett fra Adafruit
- Jeg hadde tilfeldigvis et oppladbart LiPo -batteri fra Adafruit
- Monokrom 128x32 SPI OLED -skjerm (du gjettet det: Adafruit)
- Dobbel positiv kant-utløst JK flip-flop SN74HC109 fra Texas Instruments
- Dobbel negativ kant-utløst JK flip-flop SN74HC112 fra Texas Instruments
- Firemanns- OG gate CD74AC08E fra Texas Instruments
- Firemanns ELLER gate CD74AC32E fra Texas Instruments
Trinn 3: Kretsen
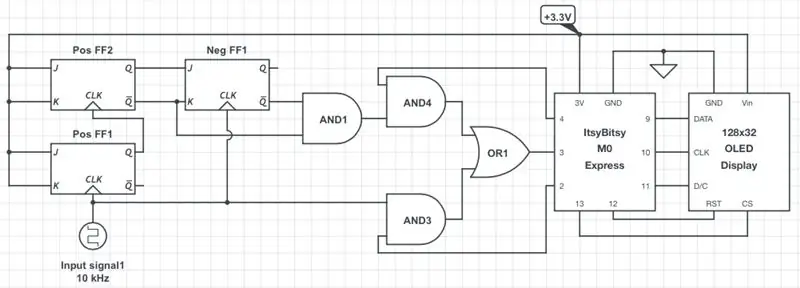
Den første figuren viser en forenklet skjematisk oversikt over frekvens/driftsmåleren. 3.3 V CMOS -logikken antas gjennomgående. Følgelig må inngangens firkantbølge amplitude være mellom den tilsvarende VIH nivå (dvs. 2 V) og 3,3 V. Hvis ikke, må du skalere den opp eller ned tilsvarende. I de fleste tilfeller vil en enkel spenningsdeler være tilstrekkelig. Hvis du vil designe din versjon av måleren på et annet logisk nivå, må du bruke en annen mikrokontroller (MCU), batteri og en skjerm som fungerer på ønsket nivå. Logikkportene og vippene som brukes i dette prosjektet, fungerer med logiske nivåer mellom 2 V og 6 V og bør være OK i de fleste tilfeller.
Som vist bruker ItsyBitsy MCU pinnene 9-13 for å kommunisere med skjermen gjennom programvare-SPI-protokollen. 3V -pinnen leverer strøm til hele kretsen. Digital inngangspinne 3 godtar det analyserte signalet, mens pinner 2 og 4 styrer signalkilden: enten direkte signal som kommer gjennom gate AND3 (lave inngangsfrekvenser), eller signal delt på 4 gjennom port AND4 (høye inngangsfrekvenser) som beskrevet i trinn 2 Koden, som ble diskutert i neste trinn, oppdager automatisk det innkommende frekvensområdet og skifter signalkilden på passende måte.
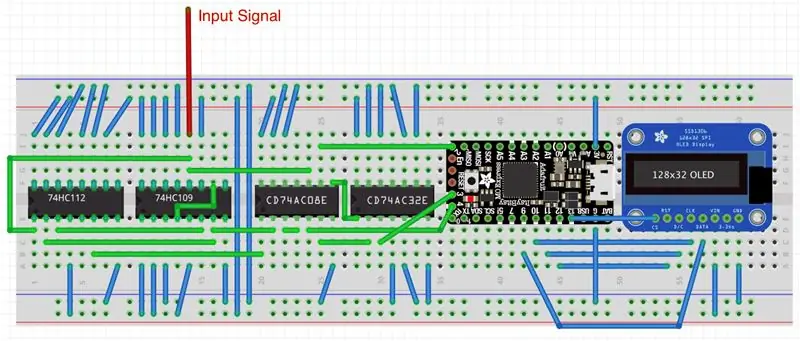
Skjematikken viser ikke den sanne kompleksiteten til digitale brikketilkoblinger. Det andre bildet viser hvordan prosjektet ville se ut på et brødbrett. Inngangssignal kommer gjennom en rød ledning til 2CLK-pinnen på den dobbelte positive kant-vippen. FORSIKTIG: Normalt skal alle J- og K -pinnene i denne vippen holdes høyt, men spesielt SN74HC109 har Kbar -pinnen - en invertert K -pinne - i stedet. Derfor må denne pinnen jordes! Den første flip-floppen med negativ kant i SN74HC112 har sin 1K- og 1J-pinne koblet til 1Q- og 1Qbar-pinnene i SN74HC109. Den andre vippen i SN74HC112 er ubrukt og inngangspinnene (2K, 2J, 2CLRbar) er jordet. Alle andre ekstra pinner PREbar (forhåndsinnstilt) og CLRbar (klar) i alle flip-flops må være koblet til logisk høy. Ubrukte klokker og utgangsstifter blir ikke tilkoblet. På samme måte er ubrukte inngangspinner i alle porter jordet, mens ubrukte utgangspinner ikke er tilkoblet. Som jeg diskuterte i min "Invisible Killer of the Phone Ring" Instruerbar, eliminerer jording av ubrukte inngangspinner av logiske brikker tilfeldige svingninger og sparer batteristrøm.
Trinn 4: Koden og måling av lave frekvenser
Naturligvis skjer all handlingen i koden som er koblet nedenfor. Når inngangen som kommer inn på pin 3 bytter fra digital lav til høy, begynner MCU å telle pulser for den interne 48 MHz -klokken. Den noterer øyeblikket for høy til lav overgang og fortsetter tellingen til neste lav til høy bryter, når den starter hele prosessen på nytt. Den første tellingen representerer pulsbredde, mens hele tellingen representerer signalets periode. Og det er hele hemmeligheten.
CPUen noterer disse overgangene via maskinvareavbrudd. SAMD21 har flere klokker; koden min bruker TC3 one. I utgangspunktet har jeg startet med å lese M0s databladstøtte for mye arbeid med å kode avbryterbehandleren, men snart har jeg oppdaget en veldig relatert kode i Arduino Forum -innleggene av brukerne electro_95, MartinL og Rucus hvis bidrag er behørig anerkjent. Jeg innlemmet og endret den kombinerte koden i min; sparer meg for mye tid!
Som jeg tidligere nevnte, er signaloppløsningen begrenset av ~ 106 CPU -sykluser for å utføre kode mellom avbrudd. Digital divisjon med pulsbreddebevaring tar seg av høye frekvenser. Lave frekvenser, på den annen side, utgjør en annen utfordring: siden TC3 -telleren er 16 bit lang, flyter den over etter å ha krysset grensen på 65, 536 tellinger. Man kan håndtere denne situasjonen ved å legge til et overløpsavbrudd, men valgte en annen løsning: TC3 kan bruke en forhåndsskaltet (dvs. programvareoppdelt) CPU-klokke i stedet for en 48 MHz maskinvare. Så hvis signalets periode nærmer seg overløpsgrensen, kan koden instruere TC3 om å bruke 24 MHz -tellinger for den neste perioden, og voila, telleren synker under 32, 768 tellinger. For enda lavere frekvenser kan TC3 instrueres til å telle 12 MHz pulser, etc. Den riktige forkalkeren bestemmes automatisk basert på signalets frekvens, med hysterese, for å holde TC3 -telleren innenfor overløpsgrensen. Som et resultat er den nedre enden av enhetens område omtrent 43 Hz.
Du er velkommen til å gaffel koden og bruke den i prosjektet ditt, men vær så snill å nevne kilden når du publiserer resultater.
Lenke til koden.
Anbefalt:
DIY -- Hvordan lage en edderkopprobot som kan kontrolleres ved hjelp av smarttelefon ved hjelp av Arduino Uno: 6 trinn

DIY || Hvordan lage en edderkopprobot som kan kontrolleres ved hjelp av smarttelefon ved hjelp av Arduino Uno: Mens du lager en edderkopprobot, kan du lære så mange ting om robotikk. Som å lage roboter er både underholdende og utfordrende. I denne videoen skal vi vise deg hvordan du lager en Spider -robot, som vi kan bruke ved hjelp av smarttelefonen vår (Androi
Hvordan lage en drone ved hjelp av Arduino UNO - Lag en quadcopter ved hjelp av mikrokontroller: 8 trinn (med bilder)

Hvordan lage en drone ved hjelp av Arduino UNO | Lag en Quadcopter ved hjelp av mikrokontroller: Introduksjon Besøk min Youtube -kanal En Drone er en veldig dyr gadget (produkt) å kjøpe. I dette innlegget skal jeg diskutere hvordan jeg får det billig? Og hvordan kan du lage din egen slik til en billig pris … Vel, i India er alle materialer (motorer, ESCer
AVR mikrokontroller. Lysdioder Blinker ved hjelp av tidtaker. Timere avbryter. Timer CTC -modus: 6 trinn

AVR mikrokontroller. Lysdioder Blinker ved hjelp av tidtaker. Timere avbryter. Timer CTC Mode: Hei alle! Timere er et viktig konsept innen elektronikk. Hver elektronisk komponent fungerer tidsmessig. Denne tidsbasen hjelper til med å holde alt arbeidet synkronisert. Alle mikrokontrollerne jobber med en forhåndsdefinert klokkefrekvens
Tastatur med LCD ved hjelp av CloudX mikrokontroller: 4 trinn
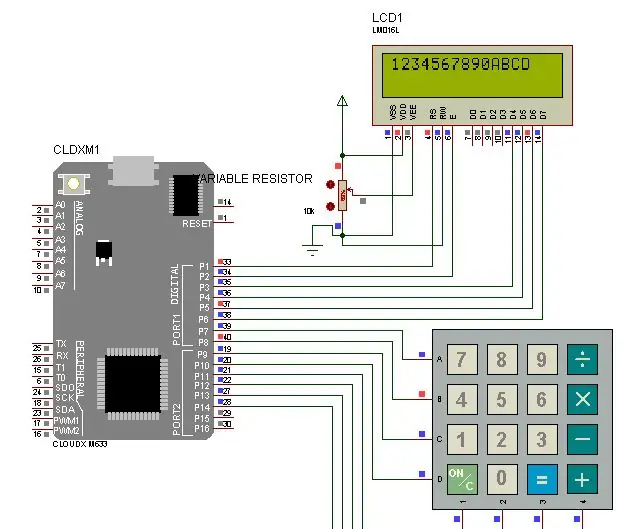
Tastatur med LCD ved hjelp av CloudX mikrokontroller: For dette prosjektet godtar vi data fra et matrisetastatur og deretter viser det på en LCD -modul
Tilpassede sølvkabler Audio/Digital/Høyfrekvens/GPS: 7 trinn

Tilpassede sølvkabler Audio/Digital/High Frequency/GPS: Med mange nye audio/video mods og nye enheter, både lyd for ipod og nå digital for video, må vi koble systemene våre til nye enheter med mer komplekse kabler. Noen veldig dyre … Disse må ha komponenter & materialer for byggeprosjekt
