
Innholdsfortegnelse:
- Trinn 1: Installere biblioteket
- Trinn 2: Fourier Transform og FFT -konsepter
- Trinn 3: Simulering av et signal
- Trinn 4: Analyse av et simulert signal - koding
- Trinn 5: Analyse av et simulert signal - Resultater
- Trinn 6: Analyse av et ekte signal - Kabling av ADC
- Trinn 7: Analyse av et ekte signal - koding
- Trinn 8: Analyse av et ekte signal - Resultater
- Trinn 9: Hva med et avskåret sinusformet signal?
- Forfatter John Day day@howwhatproduce.com.
- Public 2024-01-30 11:22.
- Sist endret 2025-01-23 15:02.


Denne relativt enkle opplæringen (med tanke på kompleksiteten i dette emnet) vil vise deg hvordan du kan lage en veldig enkel 1024 prøvespektrumanalysator ved hjelp av et Arduino -kort (1284 smal) og seriell plotter. Alle slags Arduino -kompatible brett vil gjøre, men jo mer RAM det har, den beste frekvensoppløsningen får du. Det vil trenge mer enn 8 KB RAM for å beregne FFT med 1024 prøver.
Spektrumanalyse brukes til å bestemme hovedfrekvenskomponentene i et signal. Mange lyder (som de som produseres av et musikkinstrument) består av en grunnfrekvens og noen harmoniske som har en frekvens som er et heltall multiplum av grunnfrekvensen. Spektrumanalysatoren viser deg alle disse spektrale komponentene.
Du vil kanskje bruke dette oppsettet som en frekvensmåler eller for å kontrollere alle slags signaler som du mistenker gir noe støy i din elektroniske krets.
Vi vil fokusere her på programvaredelen. Hvis du vil lage en permanent krets for en bestemt applikasjon, må du forsterke og filtrere signalet. Denne forkondisjoneringen er helt avhengig av signalet du vil studere, avhengig av amplitude, impedans, maksimal frekvens osv. Du kan sjekke
Trinn 1: Installere biblioteket
Vi kommer til å bruke ArduinoFFT -biblioteket skrevet av Enrique Condes. Siden vi ønsker å spare RAM så mye som mulig, vil vi bruke utviklingsgrenen til dette depotet som gjør det mulig å bruke float -datatypen (i stedet for dobbel) for å lagre de samplede og beregnede dataene. Så vi må installere det manuelt. Ikke bekymre deg, bare last ned arkivet og pakk det ut i Arduino -bibliotekmappen (for eksempel på Windows 10 standardkonfigurasjon: C: / Users / _your_user_name_ / Documents / Arduino / libraries)
Du kan kontrollere at biblioteket er riktig installert ved å kompilere et av eksemplene, som "FFT_01.ino."
Trinn 2: Fourier Transform og FFT -konsepter
Advarsel: Hvis du ikke tåler å se noen matematisk notasjon, vil du kanskje hoppe til trinn 3. Uansett, hvis du ikke får alt, bør du bare vurdere konklusjonen på slutten av delen.
Frekvensspekteret oppnås gjennom en Fast Fourier Transform -algoritme. FFT er en digital implementering som tilnærmer det matematiske konseptet til Fourier Transform. Under dette konseptet når du får utviklingen av et signal etter en tidsakse, kan du kjenne representasjonen i et frekvensdomene, sammensatt av komplekse (ekte + imaginære) verdier. Konseptet er gjensidig, så når du kjenner frekvensdomenerepresentasjonen, kan du transformere det tilbake til tidsdomenet og få signalet tilbake akkurat som før transformasjonen.
Men hva skal vi gjøre med dette settet med komplekse verdier i tidsdomenet? Det meste blir overlatt til ingeniører. For oss vil vi kalle en annen algoritme som vil transformere disse komplekse verdiene til spektraltetthetsdata: det er en størrelse (= intensitet) som er knyttet til hvert frekvensbånd. Antall frekvensbånd vil være det samme som antall prøver.
Du er sikkert kjent med equalizer -konseptet, som dette Tilbake til 1980 -tallet med den grafiske EQ. Vel, vi vil oppnå samme type resultater, men med 1024 bånd i stedet for 16 og mye mer intensitetsoppløsning. Når equalizeren gir et globalt syn på musikken, lar den fine spektralanalysen nøyaktig beregne intensiteten til hvert av de 1024 båndene.
Et perfekt konsept, men:
- Siden FFT er en digitalisert versjon av Fourier -transformasjonen, tilnærmer den seg det digitale signalet og mister litt informasjon. Så, strengt tatt, ville resultatet av FFT hvis det transformeres tilbake med en omvendt FFT -algoritme ikke gi akkurat det originale signalet.
- Teorien vurderer også et signal som ikke er begrenset, men som er et evigvarende konstant signal. Siden vi bare vil digitalisere det i en viss periode (dvs. prøver), vil det bli innført noen flere feil.
-
Endelig vil oppløsningen av analog til digital konvertering påvirke kvaliteten på de beregnede verdiene.
I praksis
1) Samplingsfrekvensen (notert fs)
Vi vil prøve et signal, dvs. måle amplituden, hvert 1/fs sekund. fs er samplingsfrekvensen. For eksempel hvis vi prøver ved 8 KHz, vil ADC (analog til digital omformer) som er ombord på brikken, gi en måling hvert 1/8000 sekund.
2) Antall prøver (merket N eller prøver i koden)
Siden vi trenger å få alle verdiene før vi kjører FFT, må vi lagre dem, og derfor vil vi begrense antall prøver. FFT -algoritmen trenger et antall prøver som har en effekt på 2. Jo flere prøver vi har, desto bedre, men det tar mye minne, desto mer trenger vi også for å lagre de transformerte dataene, som er komplekse verdier. Arduino FFT -biblioteket sparer litt plass ved å bruke
- En matrise kalt "vReal" for å lagre de samplede dataene og deretter den virkelige delen av de transformerte dataene
- En matrise kalt "vImag" for å lagre den imaginære delen av de transformerte dataene
Den nødvendige mengden RAM tilsvarer 2 (matriser) * 32 (bits) * N (prøver).
Så i vår Atmega1284 som har en fin 16 KB RAM, lagrer vi maksimalt N = 16000*8/64 = 2000 verdier. Siden antall verdier må være en effekt på 2, lagrer vi maksimalt 1024 verdier.
3) Frekvensoppløsningen
FFT vil beregne verdier for like mange frekvensbånd som antall prøver. Disse båndene spenner fra 0 HZ til samplingsfrekvensen (fs). Derfor er frekvensoppløsningen:
Oppløsning = fs / N
Oppløsningen er bedre når den er lavere. Så for bedre oppløsning (lavere) ønsker vi:
- flere prøver, og/eller
- en lavere fs
Men…
4) Minimal fs
Siden vi ønsker å se mange frekvenser, noen av dem er mye høyere enn den "grunnfrekvensen", kan vi ikke sette fs for lavt. Faktisk er det Nyquist - Shannon sampling setning som tvinger oss til å ha en samplingsfrekvens godt over det dobbelte av maksimal frekvens vi ønsker å teste.
For eksempel, hvis vi ønsker å analysere alt spekteret fra 0 Hz for å si 15 KHz, som er omtrent den maksimale frekvensen de fleste mennesker kan høre tydelig, må vi sette samplingsfrekvensen til 30 KHz. Faktisk setter elektronikere den ofte til 2,5 (eller til og med 2,52) * maksimal frekvens. I dette eksemplet vil det være 2,5 * 15 KHz = 37,5 KHz. Vanlige samplingsfrekvenser i profesjonell lyd er 44,1 KHz (lyd -CD -opptak), 48 KHz og mer.
Konklusjon:
Punkt 1 til 4 fører til: vi ønsker å bruke så mange prøver som mulig. I vårt tilfelle med en 16 KB RAM -enhet vil vi vurdere 1024 prøver. Vi vil prøve med den laveste samplingsfrekvensen som mulig, så lenge den er høy nok til å analysere den høyeste frekvensen vi forventer i signalet vårt (minst 2,5 * denne frekvensen).
Trinn 3: Simulering av et signal

For vårt første forsøk vil vi litt endre TFT_01.ino -eksemplet gitt i biblioteket for å analysere et signal som består av
- Grunnfrekvensen, satt til 440 Hz (musikalsk A)
- 3. harmoniske med halve kraften til det grunnleggende ("-3 dB")
- 5. harmoniske ved 1/4 av kraften til det grunnleggende ("-6 dB)
Du kan se på bildet over det resulterende signalet. Det ser virkelig veldig ut som et ekte signal man noen ganger kan se på et oscilloskop (jeg vil kalle det "Batman") i situasjoner når det er en klipping av et sinusformet signal.
Trinn 4: Analyse av et simulert signal - koding
0) Inkluder biblioteket
#inkludere "arduinoFFT.h"
1) Definisjoner
I deklarasjonsdelene har vi
const byte adcPin = 0; // A0
const uint16_t prøver = 1024; // Denne verdien MÅ ALLTID være en effekt på 2 const uint16_t samplingFrequency = 8000; // Vil påvirke tidtakerens maksimale verdi i timer_setup () SYSCLOCK/8/samplingFrekvens skal være et heltall
Siden signalet har en femte harmoniske (frekvens for denne harmoniske = 5 * 440 = 2200 Hz) må vi sette samplingsfrekvensen over 2,5 * 2200 = 5500 Hz. Her valgte jeg 8000 Hz.
Vi erklærer også matrisene der vi vil lagre rådata og beregnet data
float vReal [prøver];
float vImag [prøver];
2) Instantiering
Vi lager et ArduinoFFT -objekt. Dev -versjonen av ArduinoFFT bruker en mal, slik at vi kan bruke enten float eller den doble datatypen. Float (32 bits) er nok i forhold til den generelle presisjonen i programmet vårt.
ArduinoFFT FFT = ArduinoFFT (vReal, vImag, samples, samplingFrequency);
3) Simulering av signalet ved å fylle ut vReal -matrisen, i stedet for å ha det fylt med ADC -verdier.
I begynnelsen av løkken fyller vi vReal -matrisen med:
flyte sykluser = (((prøver) * signalFrequency) / samplingFrequency); // Antall signalsykluser som prøvetakingen vil lese
for (uint16_t i = 0; i <samples; i ++) {vReal = float ((amplitude * (sin ((i * (TWO_PI * cycles)) / samples))))) / / Bygg data med positive og negative verdier */ vReal += float ((amplitude * (sin ((3 * i * (TWO_PI * sykluser))/ prøver)))/ 2.0);/ * Bygg data med positive og negative verdier */ vReal += float ((amplitude * (sin ((5 * i * (TWO_PI * sykluser)) / prøver))) / 4.0); / * Bygg data med positive og negative verdier * / vImag = 0.0; // Imaginær del må nullstilles i tilfelle sløyfe for å unngå feilberegninger og overløp}
Vi legger til en digitalisering av grunnbølgen og de to harmoniske med mindre amplitude. Enn vi initialiserer den imaginære matrisen med nuller. Siden denne matrisen er befolket av FFT -algoritmen, må vi slette den igjen før hver ny beregning.
4) FFT -databehandling
Deretter beregner vi FFT og spektraltettheten
FFT.windowing (FFTWindow:: Hamming, FFTDirection:: Forward);
FFT.compute (FFTDirection:: Forward); / * Compute FFT */ FFT.complexToMagnitude (); / * Beregn størrelser */
FFT.windowing (…) operasjon endrer rådata fordi vi kjører FFT på et begrenset antall prøver. De første og siste prøvene presenterer en diskontinuitet (det er "ingenting" på den ene siden). Dette er en feilkilde. "Windowing" -operasjonen har en tendens til å redusere denne feilen.
FFT.compute (…) med retningen "Forward" beregner transformasjonen fra tidsdomenet til frekvensdomenet.
Deretter beregner vi størrelsesverdiene (dvs. intensiteten) for hvert av frekvensbåndene. VReal -matrisen er nå fylt med størrelsesverdier.
5) Seriell plottertegning
La oss skrive ut verdiene på serieplotteren ved å kalle funksjonen printVector (…)
PrintVector (vReal, (prøver >> 1), SCL_FREQUENCY);
Dette er en generisk funksjon som gjør det mulig å skrive ut data med en tidsakse eller en frekvensakse.
Vi skriver også ut frekvensen til båndet som har den høyeste størrelsesverdien
float x = FFT.majorPeak ();
Serial.print ("f0 ="); Serial.print (x, 6); Serial.println ("Hz");
Trinn 5: Analyse av et simulert signal - Resultater

Vi ser 3 pigger som tilsvarer grunnfrekvensen (f0), den tredje og femte harmoniske, med halvparten og 1/4 av f0 -størrelsen, som forventet. Vi kan lese øverst i vinduet f0 = 440.430114 Hz. Denne verdien er ikke akkurat 440 Hz, på grunn av alle årsakene forklart ovenfor, men den er veldig nær den virkelige verdien. Det var egentlig ikke nødvendig å vise så mange ubetydelige desimaler.
Trinn 6: Analyse av et ekte signal - Kabling av ADC

Siden vi vet hvordan vi skal gå frem i teorien, vil vi gjerne analysere et ekte signal.
Ledningen er veldig enkel. Koble bakken sammen og signallinjen til A0 -pinnen på brettet ditt gjennom en seriemotstand med en verdi på 1 KOhm til 10 KOhm.
Denne seriemotstanden vil beskytte den analoge inngangen og unngå å ringe. Det må være så høyt som mulig for å unngå ringing, og så lavt som mulig for å gi nok strøm til å lade ADC -en raskt. Se MCU -databladet for å vite den forventede impedansen til signalet som er koblet til ADC -inngangen.
For denne demoen brukte jeg en funksjonsgenerator for å mate et sinusformet signal med frekvens 440 Hz og amplitude rundt 5 volt (det er best hvis amplituden er mellom 3 og 5 volt, slik at ADC brukes nær full skala), gjennom en 1,2 KOhm motstand.
Trinn 7: Analyse av et ekte signal - koding
0) Inkluder biblioteket
#inkludere "arduinoFFT.h"
1) Erklæringer og instans
I deklarasjonsdelen definerer vi ADC -inngangen (A0), antall prøver og samplingsfrekvensen, som i forrige eksempel.
const byte adcPin = 0; // A0
const uint16_t prøver = 1024; // Denne verdien MÅ ALLTID være en effekt på 2 const uint16_t samplingFrequency = 8000; // Vil påvirke tidtakerens maksimale verdi i timer_setup () SYSCLOCK/8/samplingFrekvens skal være et heltall
Vi lager ArduinoFFT -objektet
ArduinoFFT FFT = ArduinoFFT (vReal, vImag, samples, samplingFrequency);
2) Oppsett av timer og ADC
Vi stiller inn tidtaker 1, slik at den sykler ved samplingsfrekvensen (8 KHz) og øker en avbrudd ved utgangssammenligning.
ugyldig timer_setup () {
// reset timer 1 TCCR1A = 0; TCCR1B = 0; TCNT1 = 0; TCCR1B = bit (CS11) | bit (WGM12); // CTC, prescaler på 8 TIMSK1 = bit (OCIE1B); OCR1A = ((16000000 /8) / samplingFrequency) -1; }
Og sett ADC slik det
- Bruker A0 som inngang
- Utløser automatisk på hver timer 1 -utgang sammenlign kamp B
- Genererer et avbrudd når konverteringen er fullført
ADC -klokken er satt til 1 MHz, ved å forhåndskaliere systemklokken (16 MHz) med 16. Siden hver konvertering tar omtrent 13 klokker i full skala, kan konverteringer oppnås med en frekvens på 1/13 = 0,076 MHz = 76 KHz. Samplingsfrekvensen bør være betydelig lavere enn 76 KHz for å la ADC ha tid til å samle dataene. (vi valgte fs = 8 KHz).
ugyldig adc_setup () {
ADCSRA = bit (ADEN) | bit (ADIE) | bit (ADIF); // slå på ADC, ønsker avbrudd ved fullføring ADCSRA | = bit (ADPS2); // Prescaler på 16 ADMUX = bit (REFS0) | (adcPin & 7); // innstilling av ADC -inngang ADCSRB = bit (ADTS0) | bit (ADTS2); // Timer/Counter1 Compare Match B trigger source ADCSRA | = bit (ADATE); // slå på automatisk utløsning}
Vi erklærer avbryterbehandleren som vil bli kalt etter hver ADC -konvertering for å lagre de konverterte dataene i vReal -matrisen og slette avbruddet
// ADC komplett ISR
ISR (ADC_vect) {vReal [resultNumber ++] = ADC; hvis (resultNumber == prøver) {ADCSRA = 0; // slå av ADC}} EMPTY_INTERRUPT (TIMER1_COMPB_vect);
Du kan ha en uttømmende forklaring på ADC -konvertering på Arduino (analogRead).
3) Oppsett
I oppsettfunksjonen tømmer vi den imaginære datatabellen og ringer opp timeren og ADC -oppsettfunksjonene
null I (); // en funksjon som satt til 0 alle imaginære data - forklart i forrige seksjon
timer_setup (); adc_setup ();
3) Sløyfe
FFT.dcRemoval (); // Fjern DC -komponenten i dette signalet siden ADC er referert til jord
FFT.windowing (FFTWindow:: Hamming, FFTDirection:: Forward); // Vei data FFT.compute (FFTDirection:: Forward); // Beregn FFT FFT.complexToMagnitude (); // Beregn størrelser // skrive ut spekteret og grunnfrekvensen f0 PrintVector (vReal, (prøver >> 1), SCL_FREQUENCY); float x = FFT.majorPeak (); Serial.print ("f0 ="); Serial.print (x, 6); Serial.println ("Hz");
Vi fjerner likestrømskomponenten fordi ADC refereres til jord og signalet er omtrent sentrert rundt 2,5 volt.
Deretter beregner vi dataene som forklart i forrige eksempel.
Trinn 8: Analyse av et ekte signal - Resultater

Vi ser faktisk bare en frekvens i dette enkle signalet. Den beregnede grunnfrekvensen er 440,118194 Hz. Her er verdien igjen en veldig nær tilnærming til den reelle frekvensen.
Trinn 9: Hva med et avskåret sinusformet signal?

La oss nå overdrive litt ADC ved å øke amplituden til signalet over 5 volt, så det klippes. Ikke press for mye for ikke å ødelegge ADC -inngangen!
Vi kan se noen harmoniske dukker opp. Klipping av signalet skaper høyfrekvente komponenter.
Du har sett det grunnleggende i FFT -analyse på et Arduino -kort. Nå kan du prøve å endre samplingsfrekvensen, antall prøver og vindusparameteren. Biblioteket legger også til en parameter for å beregne FFT raskere med mindre presisjon. Du vil legge merke til at hvis du setter samplingsfrekvensen for lav, vil de beregnede størrelsene virke totalt feil på grunn av spektralfolding.
Anbefalt:
DIY -- Hvordan lage en edderkopprobot som kan kontrolleres ved hjelp av smarttelefon ved hjelp av Arduino Uno: 6 trinn

DIY || Hvordan lage en edderkopprobot som kan kontrolleres ved hjelp av smarttelefon ved hjelp av Arduino Uno: Mens du lager en edderkopprobot, kan du lære så mange ting om robotikk. Som å lage roboter er både underholdende og utfordrende. I denne videoen skal vi vise deg hvordan du lager en Spider -robot, som vi kan bruke ved hjelp av smarttelefonen vår (Androi
Hvordan lage en drone ved hjelp av Arduino UNO - Lag en quadcopter ved hjelp av mikrokontroller: 8 trinn (med bilder)

Hvordan lage en drone ved hjelp av Arduino UNO | Lag en Quadcopter ved hjelp av mikrokontroller: Introduksjon Besøk min Youtube -kanal En Drone er en veldig dyr gadget (produkt) å kjøpe. I dette innlegget skal jeg diskutere hvordan jeg får det billig? Og hvordan kan du lage din egen slik til en billig pris … Vel, i India er alle materialer (motorer, ESCer
Slik prøver du å få gratis komponenter: 5 trinn
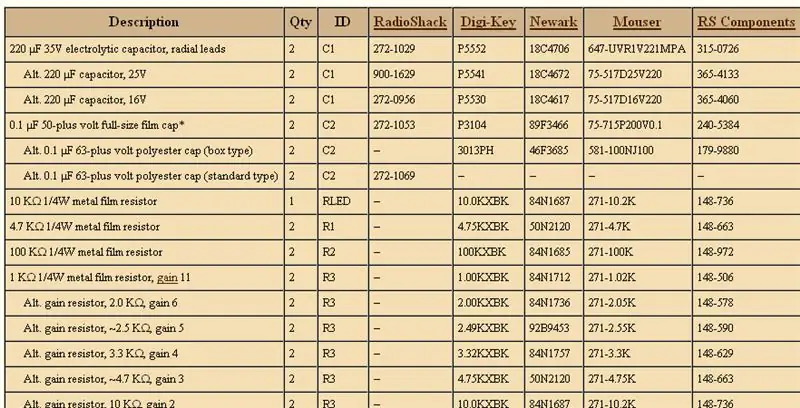
Hvordan prøve og få gratis komponenter: Noen ganger har du ikke penger, men du vil bygge noe fint. her er en guide for å hjelpe deg
Gratis elektroniske prøver: 12 trinn (med bilder)

Gratis elektroniske prøver: Visste du at noen produsenter og leverandører vil gi bort noen gratis prøver av produsentene sine til kunder og ingeniører for å teste dem på prosjektene sine? Dette er noen regler du bør vite før du begynner å få gratis prøver fra selskapet
Gratis elektroniske prøver: 5 trinn

Gratis elektroniske prøver: visste du at noen selskaper vil sende deg gratis elektronikk som lysdioder gratis? her er nettstedene jeg brukte og noen jeg plukket opp på veien
