
Innholdsfortegnelse:
- Forfatter John Day day@howwhatproduce.com.
- Public 2024-01-30 11:21.
- Sist endret 2025-01-23 15:02.



Denne instruktøren forklarer hvordan du dekoder Morse Code ved hjelp av en Arduino Uno R3.
Dekoderen, som automatisk tilpasser seg sendehastigheten, er i stand til å dekode morse opp til minst 80 ord per minutt.
Den innkommende koden vises som tekst på din Arduino Serial Monitor (eller TFT -skjerm hvis montert)
En toneoscillator er inkludert hvis du ønsker å øve på å sende morse.
Dekoderen har:
- en 320 x 240 TFT -skjermmodul [1]
- et digitalt båndpassfilter fra Goertzel for å skille uønskede signaler.
- et "Binary Morse Tree" for dekoding av signalet
- automatisk hastighetssporing
- en hørbar utgang når du trener morse
- både innkommende og utgående tekst vises.
Følgende tegn og symboler gjenkjennes:
- [A.. Z]
- [0..9]
- [., ? ' ! / () &:; = + - _ " @]
Den anslåtte kostnaden for morsekoder -skjoldet, minus TFT -skjermen, er $ 25. [1]
Bilder
- Forsidebildet viser en ferdig montert enhet
- Videoen viser dekoderen som fungerer
Merknader
[1]
- TFT -skjermmodulen er valgfri ettersom all tekst sendes til Arduino "Serial Monitor".
- TFT-modulen er beskrevet i min instruerbare
Trinn 1: Deleliste
Følgende deler ble hentet fra
1 eneste prototypeskjold for Arduino UNO R3, 2,54 mm pitch
Følgende deler ble hentet lokalt:
- 1 bare LM358 dobbel opamp
- 1 bare LED grønn
- 1 eneste LED -klips
- 1 eneste elektret mikrofonkapsel
- 1 bare normalt åpen trykknapp
- 1 bare 8-pinners DIP-kontakt
- 2 bare 330 ohm motstander
- 2 bare 2K2 motstander
- 5 bare 10K ohm motstander
- 2 bare 56K ohm motstander
- 2 bare 1uF kondensator
- 1 bare 10uF kondensator
Følgende deler er valgfrie:
- 1 bare 2,2 tommers TFT SPI LCD -skjermmodul 240*320 ILI9341 med SD -kortspor for Arduino Raspberry Pi 51/AVR/STM32/ARM/PIC [1]
- Morsetast / trykknapp
- 1 bare BC548 NPN -transistor
- 1 bare 1 tommers høyttaler
- 1 bare 33K ohm motstand
- 1 bare 3,5 mm mono -plugg (for morse -nøkkel)
- 1 bare 3,5 mm mono -kontakt (for morse -nøkkel)
- 3 bare 9 mm M3 tappede nylon avstandsstykker
- 1 bare 130 x 68 x 44 mm ABS plastboks
- 5 bare 2-pinners rettvinklede kontakter
Den anslåtte kostnaden for morsedekoder -skjoldet, minus den valgfrie TFT -skjermen, er $ 25. [1]
Merknader
[1]
Delelisten for den valgfrie 320 x 240 TFT-skjermmodulen er oppført i min instruerbare
[2]
En morselnøkkel eller solid trykknapp er nødvendig hvis du ønsker å bruke avsenderen.
Trinn 2: Kretsdiagram



Bilder
Foto 1 viser kretsdiagrammet for morsedekoderen. 330 ohm -motstanden i serie med morse -tasten begrenser D4 -utgangsstrømmen ved en tilfeldig kortslutning til bakken … øker verdien reduserer lydutgangen fra høyttaleren. Av denne grunn har jeg ikke lagt det til skjoldet, men festet det direkte til morseknappen for enkel justering
Foto 2 viser et matchende skjold. Skjoldet er fra min instruerbare https://www.instructables.com/id/Arduino-TFT-Grap… som jeg har lagt til mikrofonforsterkeren og toneoscillatoren. [1]
Foto 3 viser det ferdige skjoldet festet til en Arduino. Ingen andre komponenter kreves hvis teksten skal vises på Arduino "Serial Monitor"
Bilde 4 viser dekoderen delvis esket. Det er kuttet et hull i lokket for visning av displayet. Høyttaleren og mikrofonen har blitt limt fast til saken. Bor noen høyttalerhull i lokket før du monterer høyttaleren. Senterkontakten på lokket er for en forlengelsesmikrofon … uten dette må dekoderen plasseres nær høyttaleren, noe som ikke alltid er mulig
Bilde 5 viser TFT -skjermen. Svart elektrisk tape er festet til skjermens kanter … denne båndet forhindrer lyslekkasje og maskerer feil justering mellom displayet og åpningen i lokket
Viktig
[1]
Arduinos med en stor USB -kontakt krever et lag med elektrisk tape mellom USB -kontakten og Arduino -skjoldet. Utilsiktede shorts er mulig uten båndet, ettersom klaring er liten. Tapen er ikke nødvendig for Arduinos som har små kontakter
Trinn 3: Teori



Hver morsekodebokstav består av en serie med korte og lange varighetstoner kalt "prikker" og "bindestreker".
- en prikk (.) er 1 enhet i lengden
- en bindestrek (_) er 3 enheter i lengde
- mellomrommet mellom bokstavelementene er 1 enhet
- mellomrommet mellom bokstavene er 3 enheter
- mellomrommet mellom ord er 7 enheter
Vi kan bestemme om den innkommende tonen er prikk eller en strek ved å sammenligne varigheten med en referansetone på 2 enheter i lengde.
- en prikk er mindre enn 2 enheter
- en strek er større enn 2 enheter
Det er to helt forskjellige metoder for å dekode det innkommende mønsteret av prikker og bindestreker:
- lineært søk
- binært tre (også kjent som et dikotomisk søk)
Lineær søk
En vanlig metode er å lage en rekke tegn og deres matchende morsemønstre. For eksempel vil hvert av følgende tegn bli lagret som:
- A. _
- B _…
- C _. _.
- 0 _ _ _ _ _
- 1. _ _ _ _
- 2.. _ _ _
Hver bokstav krever 6 celler … 1 for selve bokstaven og 5 for (.) Og (_). For å gjøre dette trenger vi en bokstav [36] [6] tegnserie med totalt 216 celler. Ubrukte celler fylles normalt med et null eller et tomt.
For å dekode de innkommende prikkene og bindestrekene må vi sammenligne prikk/strekk -mønsteret for hver innkommende bokstav med våre referansetegnmønstre.
Selv om denne metoden fungerer, er den ekstremt treg.
Si at vi har 26 bokstaver ('A',.. 'Z') og sifrene ('0', … '9') lagret i en matrise, så må vi utføre 36 søk, hver med opptil 5 undersøk, som er totalt 36*5 = 180 søk for å dekode tallet '9'.
Binært tre
Et binært søk er langt raskere, ettersom ingen søk er nødvendig.
I motsetning til det lineære søket, som krever at både tegnet og morse -mønstrene lagres, lagrer det binære treet bare tegnene, noe som betyr at matrisestørrelsen er mindre.
Jeg har delt mitt binære tre (foto1) i to halvdeler (bilder 2 og 3) for å gjøre det mer lesbart.
For å finne et tegn flytter vi en peker til venstre hver gang vi hører en prikk og flytter pekeren til høyre hver gang vi hører et bindestrek. Etter hvert trekk halverer vi pekeravstanden for neste trekk … derav navnet binærtre.
For å dekode bokstaven '9' (bindestrek, bindestrek, bindestrek, prikk) krever 5 trekk … 4 til høyre og 1 til venstre som etterlater pekeren rett over '9'.
Fem trekk er betydelig raskere enn 180 søk !!!!!
Den binære tegnmatrisen er også mindre … 26 bokstaver og 10 tall krever bare en 64 x 1 linjeserie. Jeg har valgt å lage en 128 -tegners matrise slik at jeg kan dekode tegnsetting.
Trinn 4: Designnotater




Morse er vanskelig å dekode i nærvær av forstyrrende signaler. De uønskede signalene må avvises … dette krever en slags filter.
Det er mange muligheter:
- Faselåste sløyfer
- Induktorkondensatorfiltre
- Motstandskondensator aktive filtre
- Digital signalbehandling som Fast Fourier Transform eller Goertzel -filteret.
Metode 1, 2, 3 krever eksterne komponenter som er store.
Metode 4 krever ingen eksterne komponenter … frekvensene detekteres ved hjelp av matematiske algoritmer.
Fast Fourier Transform (FFT)
En metode for å oppdage tilstedeværelsen av en tone i en kompleks bølgeform er å bruke Fast Fourier Transform
Foto 1 viser hvordan FFT (Fast Fourier Transform) deler lydspekteret i “bins”.
Bilde 2 viser hvordan FFT "bingene" reagerer på et signal … i dette tilfellet 800Hz. Hvis et annet signal på si 1500Hz var til stede, ville vi se to svar … ett på 800Hz og et annet på 1500Hz.
I teorien kan en morse -kode -dekoder lages ved å overvåke utgangsnivået til en bestemt FFT -frekvensbinge … et stort tall representerer tilstedeværelsen av en prikk eller bindestrek … et lite tall representerer intet signal.
En slik morse -kode -dekoder kan lages ved å overvåke “bin 6” på bilde 2, men det er en rekke ting som er feil med denne tilnærmingen:
- vi vil bare ha en frekvensbakke … resten er bortkastede beregninger
- frekvensboksene vises kanskje ikke akkurat på frekvensen av interesse
- det er relativt tregt (20mS per Arduino -sløyfe ()
En annen metode er å bruke et Goertzel -filter.
Goertzel -filter
Goertzel -filteret ligner på FFT, men har bare en enkelt frekvensbeholder.
Foto3 viser frekvensresponsen til et Goertzel -filter for diskrete lydtrinn.
Foto 4 er et sveip av det samme filteret over det samme frekvensområdet.
Jeg bestemte meg for å "gå" med Goertzel -algoritmen som:
- Arduino loop () -tiden ved bruk av Goertzel -algoritmen var 14mS (millisekunder) mot 20mS (millisekunder) for en FFT -løsning som bruker Arduino "fix_FFT" -bibliotek.
- Det er enkelt å stille senterfrekvensen til et Goertzel båndpassfilter.
- Båndbredden er omtrent 190Hz.
Foto 5 viser den numeriske utgangen fra et 900 Hz Goertzel -filter når en tone oppdages. Jeg har satt tonen min til en verdi på 4000 … verdier over 4000 indikerer en tone.
I teorien trenger du bare å justere filteret til en behagelig lyttefrekvens. Dessverre synker lydutgangen fra min 1 tommers overvåkingshøyttaler raskt under 900Hz. For å unngå problemer bruker jeg en filterfrekvens på 950Hz. De nødvendige formlene for å beregne alternative filterfrekvenser finnes i kodehodet mitt.
Dekoding
Dekoding av prikker og bindestreker er ikke så enkelt som det ser ut først.
Perfekt morse er definert som:
- prikk = 1 enhet
- mellomrom inne i bokstaven = 1 enhet
- dash = 3 enheter
- mellomrom mellom bokstaver = 3 enheter
- mellomrom mellom ord = 7 enheter
For å dekode perfekt morse trenger vi ganske enkelt en referansetonvarighet på 2 enheter
- prikk <2 enheter
- elementrom <2 enheter
- dash> 2 enheter
- bokstav _rom> 2 enheter
- word_space> 6 enheter (dvs. 3 x referanseenheter)
Dette fungerer for maskinmors, men i den "virkelige verden":
- sendehastigheten varierer
- varigheten av hver prikk varierer
- varigheten av hver bindestrek varierer
- bokstavene E, I, S, H, 5 inneholder bare prikker som er gjennomsnittlige til prikkvarigheten
- bokstavene T, M, O, 0 inneholder bare bindestreker som gjennomsnitt til strekenes varighet
- ordgap kommer kanskje ikke
- fading skaper feil som dekoderen må gjenopprette.
- korrupte signaler på grunn av forstyrrelser
Bokstaver som bare inneholder prikker og bindestreker, løses delvis hvis:
vi estimerer referansens varighet til vi har mottatt en gyldig prikk og en gyldig bindestrek. Jeg bruker 200 millisekunder som er gyldig hvis sendehastigheten er mellom 6 WPM (ord per minutt) og 17 WPM. Du må kanskje øke denne verdien hvis du lærer morse. En hastighetstabell er inkludert i programvaren
Hastighetsvariasjoner løses hvis:
- vi utfører et rullende gjennomsnitt på hver prikk og hver bindestrek og
- beregne referansens varighet på nytt etter at hvert symbol er mottatt
Ordgap og ordgap som ikke kommer, løses hvis vi:
- husk tidspunktet for den siste bakkant (tone til no-tone) overgang,
- start algoritmen på nytt etter hver bokstav,
- beregne forløpt tid mens du venter på neste overgang (ingen tone til tone) og
- sett inn et mellomrom hvis 6 tidsenheter er overskredet.
Morse -oscillator
Jeg prøvde først noen Piezo -summer, men fant:
- frekvensen var fast
- utgangsfrekvensen var for høy for langvarig lytting
- piezos hadde en tendens til å drive ut av Goertzel -passbåndet
Jeg prøvde deretter å kjøre en akustisk transduser med en 750Hz firkantbølge, men fant at den hadde en resonans som filtrerte ut den første og tredje harmonikken. Bilde 6 viser mikrofonforsterkerens utgang til en 750Hz firkantbølge … vi ser den femte harmoniske !!!
Jeg tok deretter til en med en liten høyttaler. Foto 7 viser mikrofonutgangen til en 750Hz firkantbølge som ble sendt til en liten høyttaler … denne gangen ser vi det grunnleggende … ikke det femte harmoniske. Goertzel -filteret ignorerer alle harmoniske.
Merknader
[1]
en.wikipedia.org/wiki/Goertzel_algorithm
www.embedded.com/the-goertzel-algorithm/
Trinn 5: Programvare



Installasjon
- Last ned den vedlagte filen MorseCodeDecoder.ino [1]
- Kopier innholdet i denne filen til en ny Arduino -skisse
- Lagre skissen som "MorseCodeDecoder" (uten anførselstegn)
- Kompiler og last opp skissen til din Arduino
Programvareoppdatering 23. juli 2020
Følgende funksjoner er lagt til i den vedlagte filen "MorseCodeDecoder6.ino"
- et "Exact Blackman" -vindu [2]
- en "Noise_blanker"
Justering:
- øke mottakerens lydnivå til LED -lampen begynner å flimre og deretter slå seg av
- Still inn mottakeren din til LED -lampen blinker i takt med den innkommende morse
- Noise_blanker har blitt satt til å ignorere støybrudd opp til 8mS (en sløyfetid)
- Støygrensen kan justeres ved å sette Debug = true og se på seriell plotter
Merk
[1]
Sett Arduino Serial Monitor til 115200 bauds hvis du også vil se teksten.
[2]
- Foto 1… Eksakt Blackman -vindu
- Foto 2… Goertzel -filter uten Exact Blackman -vindu
- Foto 3,,, Goertzel -filter med Exact Blackman -vindu påført
Trinn 6: Drift
Dekoder
Plasser enheten ved siden av høyttaleren når du lytter til morse.
- Elektretmikrofonkapsel fanger opp morsesignalet fra høyttaleren din.
- Utgangen til elektretmikrofonen forsterkes deretter 647 ganger (56dB) før den sendes til Arduino for behandling.
- Et digitalt båndpassfilter fra Goertzel trekker ut morsesignalet fra støyen.
- Dekoding utføres ved hjelp av et binært tre.
- Dekoderutgangen vises som tekst på en 320 x 240 piksler TFT -skjerm. Den blir også sendt til Arduino "Serial Monitor" hvis du ikke vil bruke en skjerm.
Morse Avsender
En morsesender har også blitt inkludert. Dette lar deg øve på å sende morse og fungerer som følger:
- En konstant hørbar tone genereres på Arduino pin 4.
- Vi hører denne tonen via dekoderens høyttaler når vi trykker på morse-tasten.
- Tonen er satt til samme frekvens som Goertzel -filteret som lurer dekoderen til å tro at den lytter til ekte morse … uansett hva du sender, vil den vises som utskrevet tekst på displayet.
Sendingen din blir bedre etter hvert som dekoderen får opp vanlige feil som:
- for mye mellomrom mellom symbolene. (eksempel: Q trykt som MA)
- for mye plass mellom bokstaver (eksempel: NÅ skrives ut som NO W)
- feil kode
Trinn 7: Oppsummering
Dekoder
Denne instruksjonsboken beskriver hvordan du lager en morsekoder som konverterer morse -kode til trykt tekst.
- Dekoderen er i stand til å dekode morse opp til minst 80 WPM (ord per minutt)
- Dekoderen sporer automatisk variasjoner i mottatt sendehastighet.
- Teksten vises på seriell skjerm (eller på en 320 x 240 TFT -skjermmodul hvis montert) [1]
Avsender
En morsesender har også blitt inkludert
- Avsenderen hjelper deg med å forbedre kvaliteten på morsesendingen.
- Dekoderen bekrefter at det du har sendt er riktig
Kostnad for deler
Den estimerte kostnaden for morsedekoder -skjoldet, minus den valgfrie TFT -skjermen, er $ 25.
Klikk her for å se mine andre instrukser.


Andre pris i Audio Challenge 2020
Anbefalt:
LabDroid: Morse Code Encoder/Decoder: 4 trinn
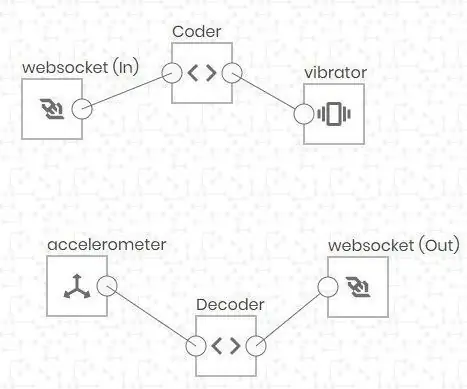
LabDroid: Morse Code Encoder/Decoder: Merk: Denne instruksjonen kan ikke realiseres 1: 1 i den nyeste versjonen av LabDroid. Jeg oppdaterer det snart. Dette prosjektet viser deg hva du kan gjøre med LabDroid. Siden en Hello World normalt er laget basert på tekst, lys eller lyd, tenkte jeg på LabDr
The Ultimate Binary Watch: 12 trinn (med bilder)

The Ultimate Binary Watch: Jeg ble nylig introdusert for begrepet binære klokker og begynte å undersøke om jeg kunne bygge en for meg selv. Imidlertid klarte jeg ikke å finne et eksisterende design som var både funksjonelt og stilig på samme tid. Så jeg bestemte meg
Escape Room Decoder Box: 7 trinn (med bilder)

Escape Room Decoder Box: Escape Rooms er utrolig morsomme aktiviteter som er veldig engasjerende og gode for lagarbeid. Har du noen gang tenkt på å lage ditt eget Escape Room? Med denne dekoderboksen kan du være godt i gang! Enda bedre har du tenkt på å bruke es
Mho Better Resistor Value Decoder Plushie: 4 trinn (med bilder)

Mho Better Resistor Value Decoder Plushie: Motstand er meningsløs, i det minste for å prøve å finne verdien av motstanden din hvis du ikke har fargekoden lagret. Jeg hadde en av disse elektroniske komponentplysjene til Adafruit Circuit Playground som lå og ventet på å bli hacke
Binary Marble Clock: 9 trinn (med bilder)

Binary Marble Clock: Dette er en enkel klokke som viser tiden (timer/minutter) i binær ved hjelp av lysdioder gjemt under glassmarmor. For en gjennomsnittlig person ser det ut som en haug med lys, men du vil kunne fortelle tiden ved å bare et raskt blikk på denne klokken. Det
