Innholdsfortegnelse:
- Forfatter John Day day@howwhatproduce.com.
- Public 2024-01-30 11:21.
- Sist endret 2025-01-23 15:02.

I denne instruksen vil jeg forklare hva et løpende gjennomsnitt er og hvorfor du bør bry deg om det, samt vise deg hvordan det skal implementeres for maksimal beregningseffektivitet (ikke bekymre deg for kompleksitet, det er veldig enkelt å forstå, og jeg vil gi et brukervennlig bibliotek for dine arduino -prosjekter også:)
Løpende gjennomsnitt, også ofte referert til som glidende gjennomsnitt, glidende gjennomsnitt eller løpende gjennomsnitt, er et begrep som brukes for å beskrive gjennomsnittlig verdi av siste N -verdier i dataserier. Den kan beregnes som et normalt gjennomsnitt, eller du kan bruke et triks for å få en minimal innvirkning på kodens ytelse.
Trinn 1: Use Case: Utjevning av ADC -målinger

Arduino har en anstendig 10 bit ADC med veldig lite støy. Når man måler verdi på en sensor som potensiometer, fotoresistor eller andre høyfjølende komponenter, er det vanskelig å stole på at målingen er korrekt.
En løsning er å ta flere målinger hver gang du vil lese sensoren din og gjennomsnittlig dem. I noen tilfeller er dette en levedyktig løsning, men ikke alltid. Hvis du ønsket å lese ADC 1000 ganger i sekundet, må du 10 000 hvis du tar gjennomsnittlig 10 målinger. Et enormt sløsing med beregningstid.
Min foreslåtte løsning er å ta målinger 1000 ganger i sekundet, oppdatere løpende gjennomsnitt hver gang og bruke den som nåværende verdi. Denne metoden introduserer litt ventetid, men reduserer beregningskompleksiteten til applikasjonen din, noe som gir deg mye mer tid til ytterligere behandling.
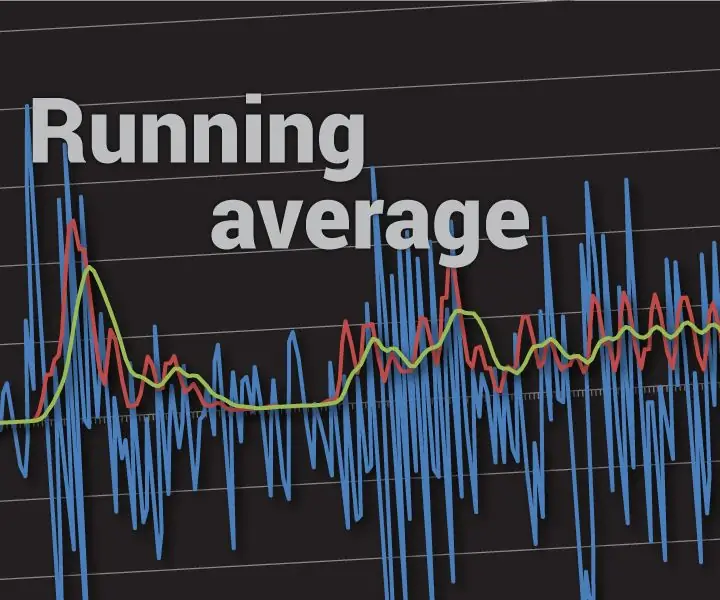
På bildet ovenfor brukte jeg løpende gjennomsnitt av de siste 32 målingene. Du vil se at denne metoden ikke er 100% feilsikker, men den forbedrer nøyaktigheten betydelig (det er ikke verre enn å gjennomsnitt 32 prøver hver gang). Hvis du ville beregne et gjennomsnitt på 32 målinger hver gang, ville det ta over 0,25 ms på Arduino UNO for målinger alene!
Trinn 2: Use Case: Measuring DC Component of Microphone Signal



Arduino kan måle spenninger mellom 0 og Vcc (normalt 5 V). Lydsignalet er helt AC, og hvis du vil måle det på en mikrokontroller, må du forspille det rundt 1/2 Vcc. I et Arduino UNO -prosjekt vil det bety omtrent 2,5 V (DC) + lydsignal (AC). Når du bruker 10 bit ADC og 5 V strømforsyning, bør 2,5 V bias være lik måling på 512. Så for å få en AC -verdi på signalet, bør 512 trekkes fra ADC -måling, og det er det, ikke sant?
I en ideell verden ville det være sant. Dessverre er det virkelige livet mer komplisert og vår signalforstyrrelse har en tendens til å drive. Svært vanlig er 50 Hz støy (60 Hz hvis du bor i USA) fra det elektriske nettverket. Vanligvis er det ikke altfor problematisk, men det er godt å vite at det eksisterer. Mer problematisk er lineær drift fra oppvarming av komponenter. Du setter nøye inn DC offset -korreksjon ved start, og den forsvinner sakte mens applikasjonen din kjører.
Jeg vil illustrere dette problemet med en (musikk) beat -detektor. Du konfigurerer fjerning av skjevhet og slag er klare (bilde 2). Etter en stund beveger DC -bias seg og slag er knapt merkbar for mikrokontrolleren (bilde 3). Slaggjenkjenningsalgoritmen vil bli utforsket grundig i en fremtidig instruksjon, ettersom den overskrider omfanget av denne artikkelen.
Heldigvis er det en måte å konstant beregne lydens DC -forskyvning. Det vil ikke komme som en overraskelse at løpende gjennomsnitt, emnet for dette instruerbare, gir en løsning.
Vi vet at gjennomsnittsverdien for ethvert vekselstrømssignal er 0. Ved å bruke denne kunnskapen kan vi trekke fra at gjennomsnittsverdien for vekselstrøm+likestrømssignal er dens likestrøm. For å fjerne det kan vi ta et løpende gjennomsnitt av de siste verdiene og trekke det fra gjeldende ADC -lesning. Vær oppmerksom på at du må bruke et langt nok løpende gjennomsnitt. For lyd bør en tiendedel av et sekund (antall prøver avhenger av samplingshastigheten) være tilstrekkelig, men vet at lengre gjennomsnitt fungerer bedre. På det første bildet kan du se eksempel på ekte DC -forspenningsberegning med løpende gjennomsnitt med 64 elementer ved 1 kHz samplingsfrekvens (mindre enn jeg anbefalte, men det fungerer fortsatt).
Trinn 3: Beregning

Du kan forestille deg løpende gjennomsnitt som gjennomsnittsvekt for mennesker på legeventerommet. Legen er ferdig med å undersøke en pasient og samtidig går en ny inn i venterommet.
For å finne ut gjennomsnittlig vekt for alle ventende pasienter i venterommet, kan sykepleier deretter spørre hver pasient om vekten deres, legge disse tallene opp og dele med antall pasienter. Hver gang legen godtar ny pasient, vil sykepleieren gjenta hele prosessen.
Du tenker kanskje: "Dette høres ikke så effektivt ut … Det må være en bedre måte å gjøre dette på." Og du ville ha rett.
For å optimalisere denne prosessen kan sykepleieren føre en oversikt over totalvekten til den nåværende pasientgruppen. Når legen har ringt den nye pasienten inn, vil sykepleieren spørre ham om vekten hans og trekke den fra gruppen totalt og la ham gå. Sykepleier ville da spørre pasienten som nettopp gikk inn i venterommet om vekten hans og legge den til summen. Gjennomsnittlig vekt på pasientene etter hvert skift vil være summen av vekter dividert med antall pasienter (ja, det samme som før, men nå spurte sykepleier bare to personer om vekten deres i stedet for dem alle). Jeg skjønner at dette avsnittet kan ha vært litt forvirrende, så se illustrasjonen ovenfor for ytterligere klarhet (eller still spørsmål i kommentarer).
Men selv om du ikke syntes det siste avsnittet var forvirrende, kan det hende du har spørsmål som hva som skal være i akkumulatoren i begynnelsen, hvordan legger jeg det jeg nettopp leste i en faktisk C -kode? Det vil bli behandlet i neste trinn, hvor du også får kildekoden min.
Trinn 4: Koden

For å beregne løpende gjennomsnitt må du først lagre de siste N -verdiene. du kan ha en matrise med N -elementer og flytte hele innholdet ett sted hver gang du legger til et element (ikke gjør dette), eller du kan overskrive et gammelt element og justere pekeren til neste element som skal kastes (vær så snill å gjøre dette:)
Akkumulator bør starte initialisert til 0, det samme gjelder for alle elementer i forsinkelseslinje. I andre tilfeller vil løpende gjennomsnitt alltid være feil. Du vil se at delayLine_init tar seg av å initialisere forsinkelseslinjen, du bør ta vare på akkumulatoren selv.
å legge til et element for å forsinke linjen er like enkelt som å redusere indeksen til det nyeste elementet med 1, og sørg for at det ikke peker på siden av forsinkelseslinjematrisen. etter å ha redusert indeksen når den er 0, vil den gå rundt til 255 (fordi det er et 8 -bits usignert heltall). Modulo (%) -operatør med størrelsen på forsinkelseslinjeserien vil sikre at indeksen peker til et gyldig element.
Å beregne et løpende gjennomsnitt bør være lett å forstå hvis du fulgte analogien min i forrige trinn. Trekk det eldste elementet fra akkumulatoren, legg den nyeste verdien til akkumulatoren, skyv den nyeste verdien til forsinkelseslinjen, returner akkumulatoren delt på antall elementer.
Lett, ikke sant?
Du er velkommen til å eksperimentere med å bruke den vedlagte koden for å bedre forstå hvordan alt dette fungerer. Slik det er nå, leser arduino analog verdi på analog pin A0 og skriver ut "[ADC -verdi], [løpende gjennomsnitt]" på seriell port med 115200 baudhastighet. Hvis du åpner arduinos serielle plotter med riktig overføringshastighet, ser du to linjer: ADC -verdi (blå) og utjevnet verdi (rød).
Trinn 5: Tillegg

Det er noen få ting du ikke nødvendigvis trenger å vite for å bruke løpende gjennomsnitt i prosjektet ditt. Det vil ikke skade å vite.
forsinkelse: Jeg vil begynne med å snakke om illustrasjon av dette trinnet. Du vil legge merke til at løpende gjennomsnitt av flere elementer gir større forsinkelse. Hvis responstiden din for å endre verdi er kritisk, vil du kanskje bruke et kortere løpende gjennomsnitt eller øke samplingsfrekvensen (mål oftere).
Går videre.
initialisering: Da jeg snakket om initialisering av akkumulator og forsinkelseselementer, sa jeg at du skulle initialisere dem alle til 0. Alternativt kan du initialisere forsinkelseslinjen til alt du liker, men akkumulatoren skal starte som en sum av de nyeste N -elementene i forsinkelseslinjen (hvor N er antall elementer i løpende gjennomsnitt). Hvis akkumulator starter som en hvilken som helst annen verdi, vil beregnet gjennomsnitt være feil - enten for lavt eller for høyt, alltid med samme beløp (forutsatt de samme innledende forholdene). Jeg foreslår at du prøver å lære hvorfor dette er slik ved å bruke noen "penn og papirsimulering".
akkumulatorstørrelse: Du bør også merke deg at akkumulatoren skal være stor nok til å lagre summen av alle elementene i forsinkelseslinjen hvis de alle er positive eller negative maks. Det betyr praktisk talt at akkumulator skal være én datatype større enn forsinkelseslinjeelementer og signert hvis forsinkelseslinjeelementer er signert.
triks: Lange forsinkelseslinjer tar mye minne. Det kan fort bli et problem. Hvis du er svært begrenset med hukommelse og ikke bryr deg så mye om nøyaktighet, kan du tilnærme løpende gjennomsnitt ved å utelate forsinkelse helt og gjøre dette i stedet: trekk 1/N * akkumulator fra akkumulatoren og legg til ny verdi (på eksempel på 8 langt løpende gjennomsnitt: akkumulator = akkumulator * 7/8 + newValue). Denne metoden gir feil resultat, men det er en grei metode for å beregne løpende gjennomsnitt når du har lite minne.
lingvistikk: "løpende gjennomsnitt/gjennomsnitt" brukes vanligvis når det refereres til gjennomsnittlig sanntid mens "glidende gjennomsnitt/gjennomsnitt" vanligvis betyr at algoritmen kjører på statiske datasett, for eksempel Excel -regneark.
Trinn 6: Konklusjon
Jeg håper dette var lett å forstå, og at det vil hjelpe deg i dine fremtidige prosjekter. Send gjerne spørsmål i kommentarene nedenfor hvis det er noe uklart.
Anbefalt:
Velg en tittel og søkeord for instruksjonene dine: 6 trinn (med bilder)

Velg en tittel og nøkkelord for instruksjonsboken din: Å velge riktig tittel og søkeord kan være forskjellen mellom en instruerbar å gå til forsiden av Googles søkeresultater eller krasje og brenne seg inn i det fryktede, no-views-landet til internettene. Mens søkeord og tittel ikke er de eneste
Koble til og ettermonter dine tilkoblede løsninger med Hologram Nova og Ubidots: 9 trinn

Koble til og ettermonter dine tilkoblede løsninger med Hologram Nova og Ubidots: Bruk Hologram Nova til å ettermontere infrastruktur. Sett opp Hologram Nova ved hjelp av en Raspberry Pi for å sende (temperatur) data til Ubidots. I den følgende veiledningen vil Ubidots demonstrere hvordan du konfigurerer et Hologram Nova ved hjelp av en Raspberry Pi og viser en te
Lag dine egne widgets enkelt - Rask BPM -teller: 6 trinn
Lag dine egne widgets enkelt - Rask BPM -teller: Web -apper er vanlige, men ikke nettapper som ikke krever internettilgang. I denne artikkelen viser jeg deg hvordan jeg lagde en BPM -teller i en enkel HTML -side kombinert med vanilje -javascript ( se her). Hvis den er lastet ned, kan denne widgeten brukes offline
Hvordan lage dine egne PCB -er: 7 trinn
Hvordan lage dine egne PCB -er: I denne opplæringen vil jeg vise deg hvordan du kan designe dine egne PCB -er på få minutter
CP2 Excel veid gjennomsnitt: 14 trinn
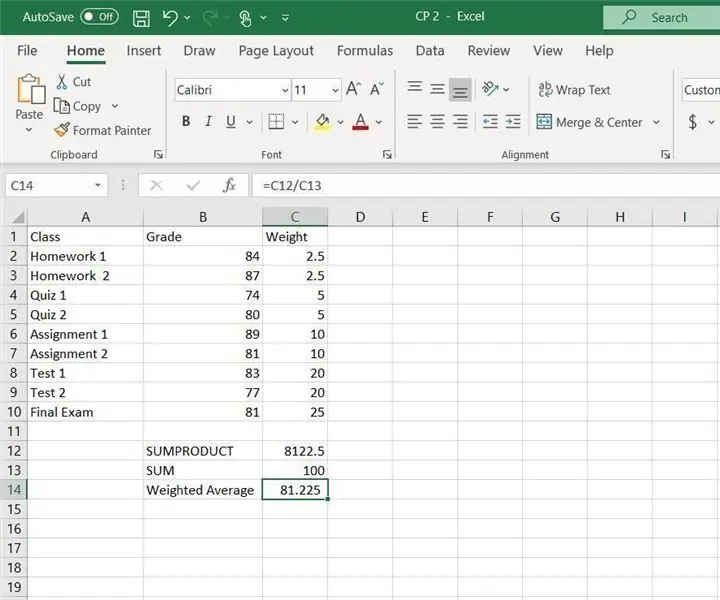
CP2 Excel veid gjennomsnitt: Instruksjoner om hvordan du beregner det veide gjennomsnittet i Excel. I dette eksemplet vil SUMPRODUCT og SUM -funksjonen bli brukt i Excel. Det veide gjennomsnittet er nyttig for å beregne totalkarakteren for en klasse
