Eksperimenter i avansert datalogging (ved hjelp av Python): 11 trinn

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-30 11:21

Det er mange dataloggingsinstruksjoner, så da jeg ønsket å bygge et eget loggprosjekt, så jeg meg rundt på en haug. Noen var gode, noen ikke så mye, så jeg bestemte meg for å ta noen av de bedre ideene og lage min egen søknad. Dette resulterte i et prosjekt både mer avansert og mer komplisert enn jeg først hadde forventet. En del av det ble en serie eksperimenter i behandling av sensordata. Denne instruksen lar deg prøve de samme eller lignende eksperimentene.

(Du kan se all koden og laste den ned på: Kode på GitHub Du kan komme til visning, kanskje i et annet vindu, med bare 2 klikk)

Vanligvis innebærer datalogging følgende:

• Datainnsamling: Les noen data fra en sensor. Ofte er dette bare å lese en analog til digital omformer (ADC) på en enhet som en Arduino.
• Databehandling: Når du leser en ADC -verdi, må konverteringsutgangen normalt skaleres til de riktige enhetene. Det kan også være behov for å gjøre noen justeringer for å kalibrere verdiene som skal korrigeres for sensorfeil.
• Filtrering: Data inneholder vanligvis noe støy, dette kan filtreres slik at du ser etter signalet i dataene dine, ikke støyen.
• Datalagring: Dataene lagres, kanskje i en tekstfil, kanskje i skyen. Data bør overleve selv om strømmen går av. Det er enkelt å lagre for mye data, vi har et lite triks for å redusere datalagringsplassen.
• Datavisning: Metoder for å se på dataene dine, egentlig ikke datalogging, men hvis du ikke gjør noen form for visning av dataene, hvorfor samle dem?
• Fjernadgang: Ikke nødvendig, men hyggelig å ha.

De fleste instruktører inkluderer noen, men ikke alle de ovennevnte, eller gjør dem på en veldig enkel måte. Denne instruksen tar for seg to av de ofte hoppede loggproblemene, og gir deg som en bonus et diagram for å grafisere dataene dine uten å bruke en skytjeneste. Du kan bruke det hele eller trekke ut biter og remixe dem til et eget prosjekt.

Trinn 1: Verktøy og materialer

Dette eksemplet er alt i Python, så det vil kjøre på, og komponenter kan brukes på, stort sett alle operativsystemer, inkludert Mac, PC, Linux og Raspberry Pi.

Så for å bruke denne instruerbare alt du trenger er et Python 3.6 -miljø som kjører, og last ned den vedlagte koden. Etter å ha kjørt koden jeg har satt opp, kan du endre den for dine egne eksperimenter. Som vanlig med Python må du kanskje legge til noen pakker/moduler for å få alt til å fungere. Mitt Spyder -miljø har stort sett alle nødvendige deler på plass (se: Graph Instructable Views with Python Screen Scraping). Når du først ser på feilmeldinger, vil de gi deg beskjed om manglende deler i miljøet ditt.

De to neste trinnene vil fortelle deg hvordan du bygger og kjører et eget eksperiment, men det er sannsynligvis bedre å vente til du kjører de inkluderte eksperimentene før du prøver ditt eget.

For å forstå koden må du ha litt erfaring med objektorientert Python, og forklare at det er utenfor omfanget av denne instruerbare, men Google bør gi deg all hjelp du måtte trenge.

Legg merke til koden: (Kode på GitHub Du kan komme til visning, kanskje i et annet vindu, med bare 2 klikk) er nå i Python 3.6, så det vil være best å ha 3,6. Eldre versjon av koden er her i koblingene nedenfor.

Trinn 2: Bygg et eksperiment

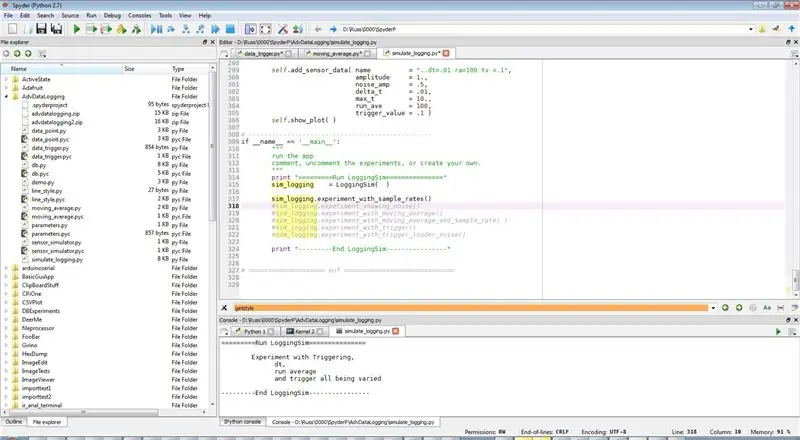
Det er tre programmeringstrinn (og linjer) for å bygge et eksperiment. Hvert eksperiment er en funksjon i LoggingSim -objektet i filen simulate_logging.py. La oss se på eksperiment 1 (bare den første grafen) som vi vil kjøre i neste trinn:

def experiment_with_sample_rates (self):

print "" "Eksperimenter med prøvepriser Ser på forskjellige samplingshastigheter ved å endre delta T" "" self.start_plot (plot_title = "Prøvepriser - del 1/3: Delta T = 1.0") self.add_sensor_data (name = "dt = 1. ", amplitude = 1., noise_amp =.0, delta_t = 1., max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot ()

Hvert eksperiment er skrevet som sin egen funksjon, så vi har en linje som definerer funksjonen (def eksperiment …..)

Den neste, ikke -kommentarlinjen, (start_plot (….) lager objektet for eksperimentet og gir det et navn.

Den neste linjen, uten kommentar, (add_sensor_data (…) er delt inn i flere linjer. Den simulerer en sensor som måler et signal med potensielt støy og noe prosessering. Funksjonsargumentene er som følger:

• navn: et navn på den siste grafen for å identifisere dataene
• amplitude: hvor stort signalet er, vil vi alltid bruke en amplitude på 1. i denne instruerbare.
• noise_amp: hvor stor støyen er, 0. er ingen støy, vi starter her.
• delta_t: tiden mellom målingene, kontrollerer samplingshastigheten.
• max_t: maksimal tid vi samler inn data, vil vi alltid bruke 10 i denne instruksen.
• run_ave: behandling med et løpende gjennomsnitt, 0 betyr ingen behandling.
• trigger_value: behandling ved hjelp av triggering, 0 betyr ingen behandling

den siste linjen, uten kommentar, (self.show_plot ……) viser grafen.

For å gjøre ting litt mer komplisert kan du ha flere linjer på en graf eller flere grafer i et eksperiment. Dette bør være tydelig fra eksperimentene som følger.

Trinn 3: Kjøre et eksperiment

Dette er koden for å kjøre et eksperiment. Som vanlig i Python er den plassert på slutten av filen.

sim_logging = LoggingSim ()

sim_logging.experiment_with_sample_rates ()

Dette er bare 2 linjer:

• Lag en loggesimulator (LoggingSim ())
• Kjør den (sim_logging.experiment_with_sample_rates ())

I den nedlastede koden har jeg noen flere linjer og kommentarer, det burde være lett å finne ut.

Trinn 4: Eksperiment: Prøvehastighet

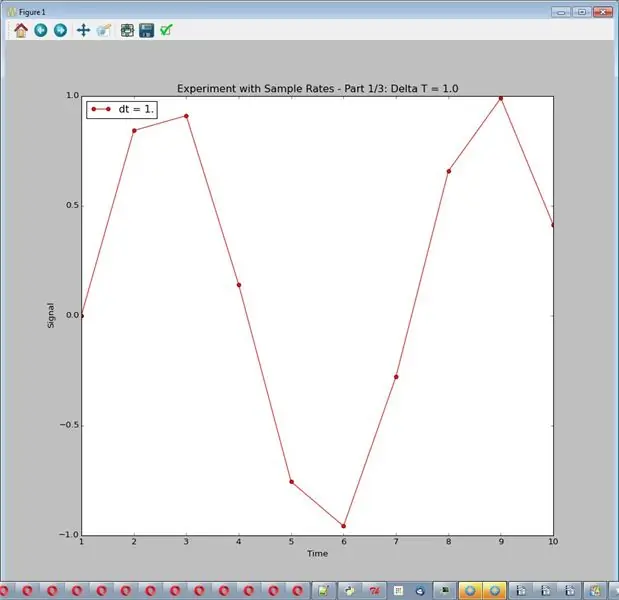
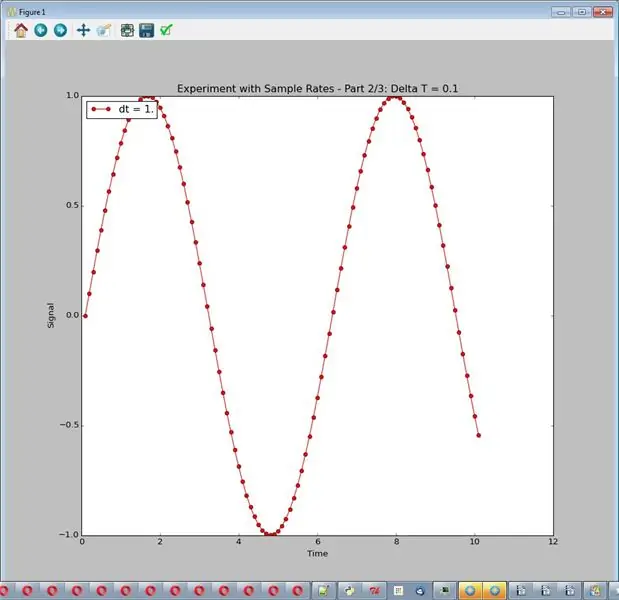
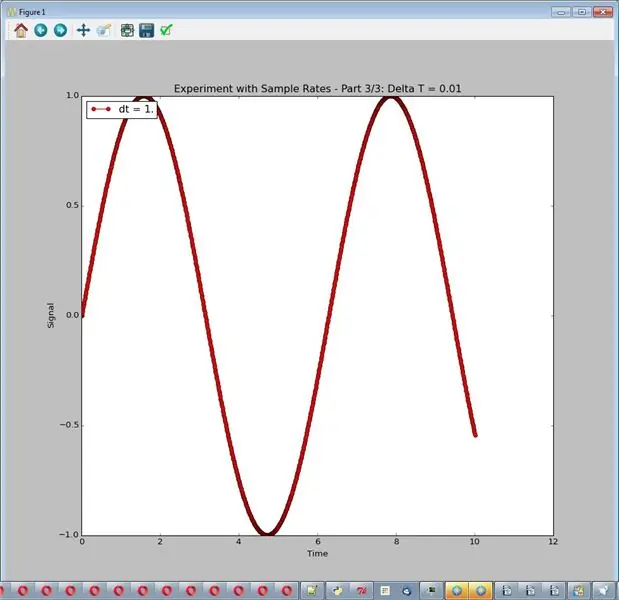
Simulatoren, slik den er satt opp her, gir alltid ut en fin jevn sinusbølge med amplitude 1. For dette eksperimentet vil vi rote med samplingshastigheten, justert med delta_t, tidsforskjellen mellom prøvene. Vi vil ikke ha støy eller annen behandling. Koden bruker 3 samplingsfrekvenser (delta_t = 1.0, 0.1 og 0.01.) Siden grafene faller oppå hverandre er eksperimentet satt opp for å produsere 3 forskjellige grafer. De resulterende grafene er bildene for dette trinnet.

def experiment_with_sample_rates (self):

print "" "Eksperimenter med prøvepriser Ser på forskjellige samplingshastigheter ved å endre delta T" "" self.start_plot (plot_title = "Eksempel på prøvepriser 1/3: Delta T = 1.0") self.add_sensor_data (name = "dt = 1. ", amplitude = 1., noise_amp =.0, delta_t = 1., max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot () # ------------- ----------------------------------- self.start_plot (plot_title = "Eksempelpriser 2/3: Delta T = 0,1 ") self.add_sensor_data (navn =" dt = 1. ", amplitude = 1., noise_amp =.0, delta_t = 0.1, max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot () # ------------------------------------------------ selv.start_plot (plot_title = "Eksempeleksempelpriser 3/3: Delta T = 0.01") self.add_sensor_data (navn = "dt = 1.", amplitude = 1., noise_amp =.0, delta_t = 0.01, max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot ()

For å kjøre den, bruk linjen: sim_logging.experiment_with_sample_rates ()

Mulige konklusjoner:

• For lav samplingsfrekvens er virkelig dårlig.
• Høye priser er ofte bedre.

(Python 3.6 -kode på GitHub -lenken nedenfor på instructables, 2.7)

Trinn 5: Eksperiment: Viser støy

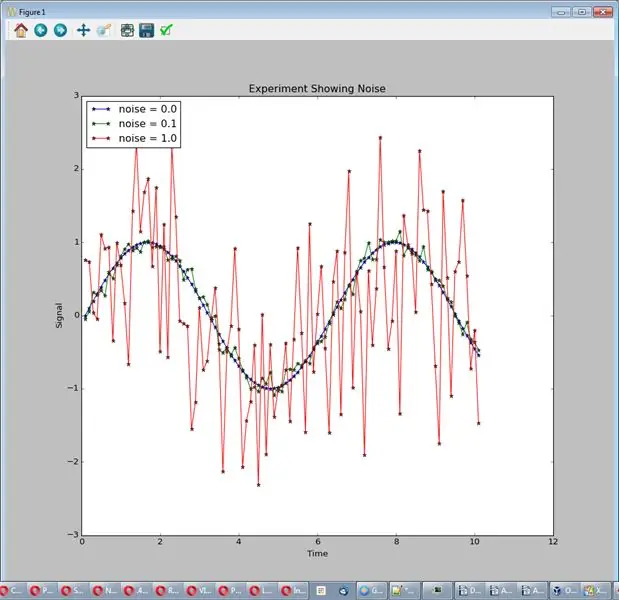
I dette eksperimentet beholder vi det samme signalet, bruker en middels samplingshastighet og har forskjellige mengder støy (noise_amp =.0,.1, 1.0.) Kjør det med: sim_logging.experiment_showing_noise (). Utgangen er en graf med 3 linjer.

Mulig konklusjon:

Støy gjør det vanskelig å se signalet, reduser det hvis du kan

Koden:

# ------------------------------------------------

def experiment_showing_noise (self): print "" "Eksperiment som viser støy Ser på forskjellige mengder støy ved å endre støyamplituden." "" self.start_plot (plot_title = "Experiment som viser støy") self.add_sensor_data (name = "noise = 0.0 ", amplitude = 1., noise_amp =.0, delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.add_sensor_data (navn =" noise = 0.1 ", amplitude = 1., noise_amp =. 1, delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.add_sensor_data (navn = "noise = 1.0", amplitude = 1., noise_amp = 1., delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot ()

Trinn 6: Eksperiment: Reduser støy med glidende gjennomsnitt

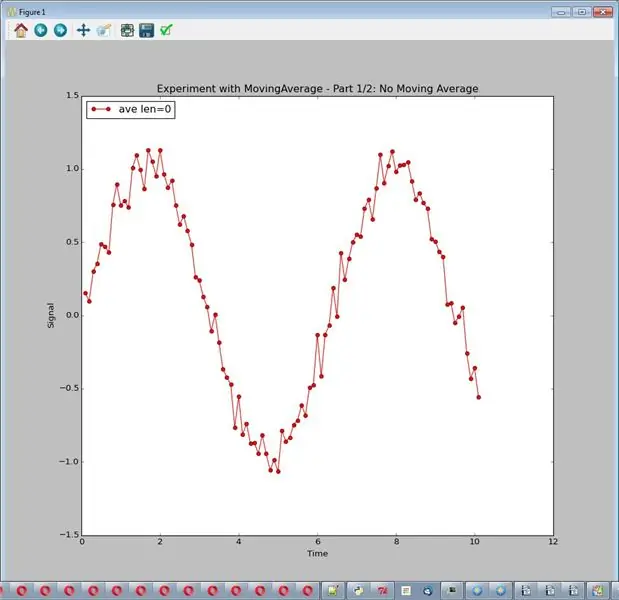
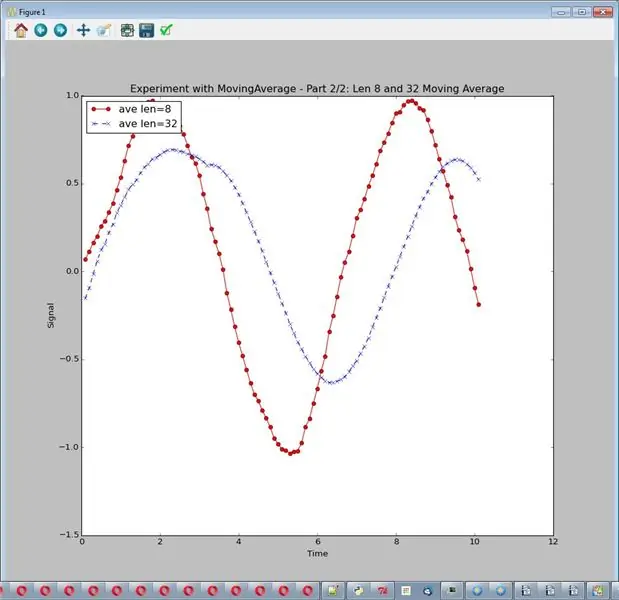
Et glidende gjennomsnitt (for eksempel med lengde 8) tar de siste 8 målingene og gjennomsnitt dem. Hvis støyen er tilfeldig, håper vi at den vil bli gjennomsnittlig til nær 0. Kjør eksperimentet med: sim_logging.experiment_showing_noise (). Skriv ut en graf.

Mulige konklusjoner:

• Et glidende gjennomsnitt eliminerer mye av støyen
• Jo lenger det glidende gjennomsnittet er, jo mer støyreduksjon
• Det lengre glidende gjennomsnittet kan redusere og forvride signalet

Koden:

# ------------------------------------------------

def experiment_with_moving_average (self): print "" "Experiment with MovingAverage Ser på forskjellige MovingAverage ved å endre lengden. Alle har samme støy." "" # ------------------ ------------------------------ self.start_plot (plot_title = "MovingAverage-Part 1/2: No Moving Average") selv.add_sensor_data (navn = "ave len = 0", amplitude = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.show_plot () self.start_plot (plot_title) = "MovingAverage-Part 2/2: Len 8 og 32") self.add_sensor_data (navn = "ave len = 8", amplitude = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 8, trigger_value = 0) self.add_sensor_data (navn = "ave len = 32", amplitude = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 32, trigger_value = 0) self.show_plot ()

Trinn 7: Eksperiment: glidende gjennomsnitt og prøvehastighet

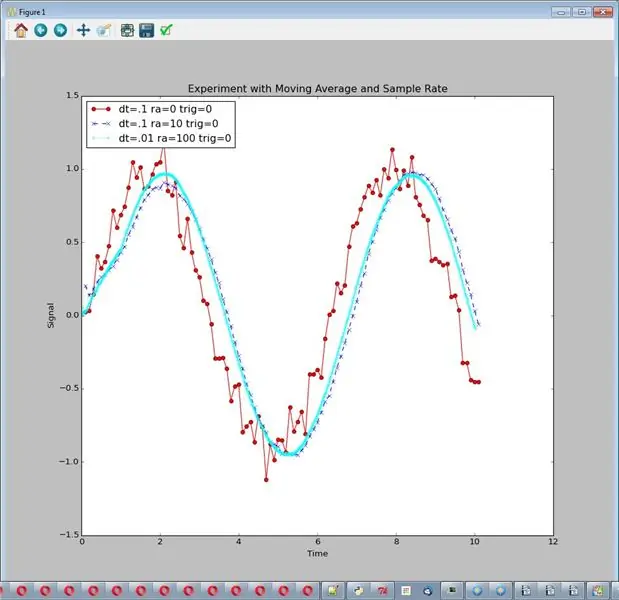
I dette eksperimentet sammenligner vi råsignalet med støy og 2 forskjellige variasjoner for å redusere støyen.

1. Middels prøvehastighet og middels løpende gjennomsnitt
2. Høy prøvehastighet og løpende gjennomsnittlig høy lengde

Kjør den med: sim_logging …… Output er en graf. Jeg tror det er klart at #2 gjør en bedre jobb med å redusere støyen, så vi kan konkludere med at:

Høy samplingshastighet og løpende gjennomsnitt med høy lengde er gode

Men du må huske på at det er en kostnad. #2 tar mye mer behandling og resulterer i at mye mer data lagres. Kostnaden kan være verdt det eller ikke. I det neste eksperimentet vil vi legge til en trigger, en enhet for å redusere mengden data som er lagret.

Koden:

def experiment_with_moving_average_and_sample_rate (self):

print "" "Eksperimenter med glidende gjennomsnitt og prøvehastighet, dt, kjøre gjennomsnitt som varieres" "" # ---------------------------- -------------------- self.start_plot (plot_title = "Moving Average and Sample Rate") self.add_sensor_data (name = "dt =.1 ra = 0 trig = 0 ", amplitude = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 0, trigger_value = 0) self.add_sensor_data (navn =" dt =.1 ra = 10 trig = 0 ", amplitude = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 10, trigger_value = 0) self.add_sensor_data (navn = "dt =.01 ra = 100 trig = 0", amplitude = 1., noise_amp =.1, delta_t =.01, max_t = 10., run_ave = 100, trigger_value = 0) self.show_plot ()

Trinn 8: Eksperiment: Logging med utløser

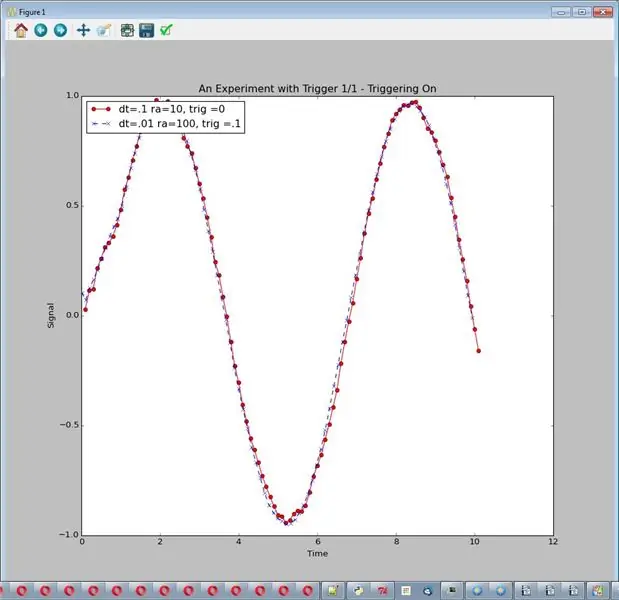
I dette eksperimentet legger vi til en trigger. For det første, hva mener jeg med en trigger? En trigger er en teknikk der vi samler inn data, men bare lagrer dem etter at en variabel har endret seg betydelig. I disse eksperimentene satte jeg en trigger på variabelen tid (x -akse). Ved å bruke utløseren kan jeg ta den høye datamengden fra rask sampling og redusere den til en mer rimelig mengde data. Det er spesielt nyttig med høye samplingshastigheter og et langt løpende gjennomsnitt.

Jeg har tatt #2 -linjen fra det siste eksperimentet som var "bra" og la til en trigger. Kjør den med: sim_logging …… Utdata er en graf, x linjer.

Hva skjer? Vi får et "godt" plot med en rimelig mengde data (det samme som nr. 1). Det har vært en del kostnader ved høyere behandling. Totalt sett er imidlertid resultatene omtrent det samme som #1 den lavere samplingshastigheten med mindre filtrering. Du kan konkludere med:

• Langt løpende gjennomsnitt med utløser kan gi god støydemping med rimelige mengder data.
• Den ekstra behandlingen gir kanskje ikke så mye bedre resultater og kommer med en kostnad.

Koden:

# ------------------------------------------------

def experiment_with_trigger (self): print "" "" Experiment with Triggering, dt, run average and trigger all being variety "" " # ----------------------- ------------------------- self.start_plot (plot_title = "Trigger 1/1-Triggering On") self.add_sensor_data (name = "dt =.1 ra = 10, trig = 0 ", amplitude = 1., noise_amp =.1, delta_t =.1, max_t = 10., run_ave = 10, trigger_value = 0) self.add_sensor_data (navn =" dt =.01 ra = 100, trig =.1 ", amplitude = 1., noise_amp =.1, delta_t =.01, max_t = 10., run_ave = 100, trigger_value =.1) self.show_plot ()

=

Trinn 9: Eksperiment: Logging With Trigger - Louder Noise

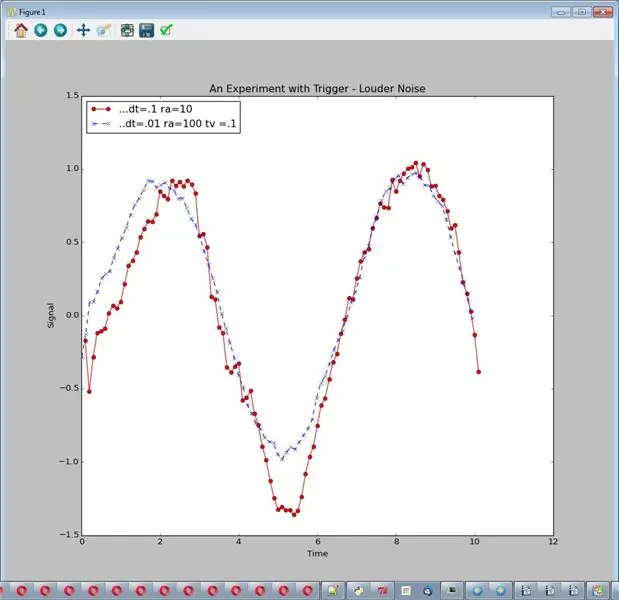
La oss ta det samme eksperimentet som det siste trinnet og forsterke støyen. Kjør den med: sim_logging …… Utdata er en graf, 2 linjer.

Nå ser den ekstra behandlingen mer verdt ut. En rimelig konklusjon her kan være:

Å velge mengde og type behandling for støyreduksjon avhenger av signalet og støyen

Koden:

def experiment_with_trigger_louder_noise (self):

print "" "Høyere støy enn tidligere eksperiment" "" self.start_plot (plot_title = "Et eksperiment med Trigger-Louder Noise") self.add_sensor_data (navn = "… dt =.1 ra = 10", amplitude = 1., noise_amp =.5, delta_t =.1, max_t = 10., run_ave = 10, trigger_value = 0) self.add_sensor_data (navn = "..dt =.01 ra = 100 tv =.1", amplitude = 1., noise_amp =.5, delta_t =.01, max_t = 10., run_ave = 100, trigger_value =.1) self.show_plot ()

Trinn 10: Lag dine egne eksperimenter

På dette tidspunktet håper jeg at du ser at teknikkene i denne instruksjonsboken kan være nyttige i datalogging, men at de også må brukes med tanke. Å eksperimentere med dem kan hjelpe denne prosessen.

Noen kommentarer til eksperimentene og ting du kan se nærmere på:

• Sinusbølger er ikke den eneste interessante signaltypen, prøv andre, andre bølger eller ramper eller…..
• Jeg brukte en normal fordeling for støyen, det er så mange typer støy; du bør vurdere andre
• Å kjøre gjennomsnitt er en enkel, men ikke den eneste metoden for å se på støy

Merk: logging av bilder fra Wikipedia.

Trinn 11: Bruke teknikkene i loggprogramvaren

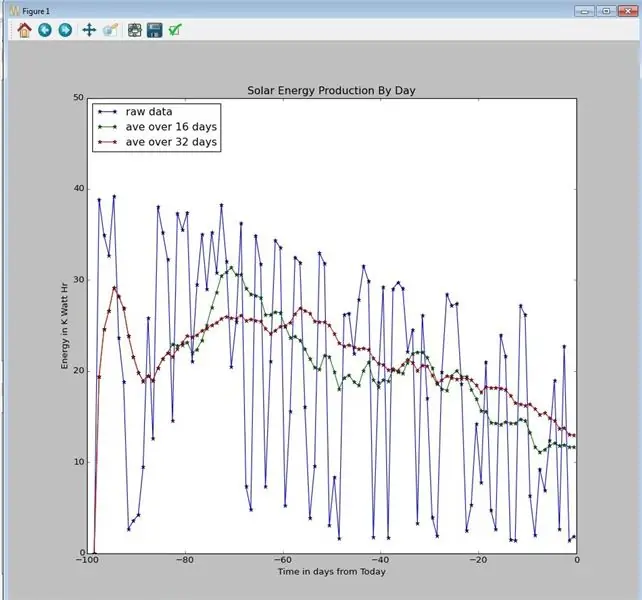
Koden min er objektorientert og behandlingen for løpende gjennomsnitt og trigger kan bare kopieres til Python -miljøet ditt og deretter brukes. Objektene er:

• DataTrigger i data_trigger.py
• MovingAverage i moving_average.py

Hovedobjektet mitt LoggingSim i simulate_logging.py skal gi deg et godt eksempel på hvordan du bruker det. Hvis du bruker et annet språk, kan du lese koden min og implementere på ditt språk.

Denne koden kan gi prosjektet bedre datalogging, prøv det.

Grafen ovenfor er fra Graph Your Solar Power av russ_hensel som bruker det samme løpende gjennomsnittlige objektet.