☠WEEDINATOR☠ Del 4: Differensiell styringsgeometri -kode: 3 trinn

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-30 11:25

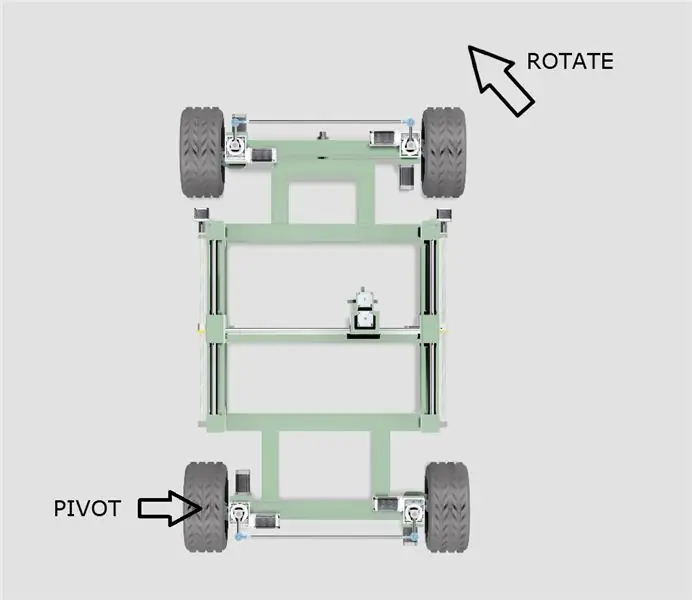
Hvis du har tid til å se videoen ovenfor, vil du legge merke til at det er noen merkelige lyder forårsaket av motorene på rattet som stopper nå og da WEEDINATOR navigerer en 3 -punkts sving. Motorene støter i hovedsak mot hverandre ettersom svingradiusen er forskjellig på innsiden til utsiden og avstanden hjulet beveger seg er forskjellig per svingningsgrad.

Svingens geometri kan utarbeides ved å skissere rundt 8 permutasjoner av svingen, og gi eksempler på sving i forskjellige vinkler på det indre hjulet fra 0 (ingen sving) til 90 (full lås) grader. Høres komplisert ut?

De fleste roboter med små hjul prøver ikke å ha noen form for sofistikert styring og er veldig effektive på å bare endre den relative hastigheten til motorene på hver side av kjøretøyet, noe som er omtrent det samme som hvordan en beltegraver eller tank virker. Dette er flott hvis du lader over en kraterfylt krigssone og skyter på alt som beveger seg, men i et rolig landbruksmiljø er det viktig å gjøre så lite skade på jord og bakken som mulig, så sliping av hjul frem og tilbake mot hverandre er ikke passende!

De fleste biler og traktorer har en veldig nyttig gadget som kalles en "differensial", bortsett fra bilene du ser i gamle amerikanske filmer hvor du kan høre dekkene som skriker hver gang de går rundt et hjørne. Bygger amerikanerne fortsatt biler som dette? Med WEEDINATOR kan vi programmere differensial i drivmotorene ved å beregne formelen for de relative hastighetene og vinklene til hjulene i en bestemt svingningsvinkel. Høres det fortsatt komplisert ut?

Her er et raskt eksempel:

Hvis WEEDINATOR navigerer en sving og har det innvendige hjulet på 45 grader, er det ytre hjulet IKKE 45 grader, det er mer som 30 grader. Det indre hjulet kan også snu i 1 km/time, men det ytre hjulet vil være betydelig raskere, mer som 1,35 km/time.

Trinn 1: Oppsett av geometri

Noen få grunnleggende antagelser er gjort til å begynne med:

• Chassiset vil svinge rundt ett av bakhjulene som vist i diagrammet ovenfor.
• Det effektive midten av svingesirkelen vil bevege seg langs en linje som strekker seg fra midten av de to bakhjulene, avhengig av svingvinkelen.
• Geometrien vil ha form av en sinuskurve.

Trinn 2: Skalerte tegninger av hjulvinkler og radier

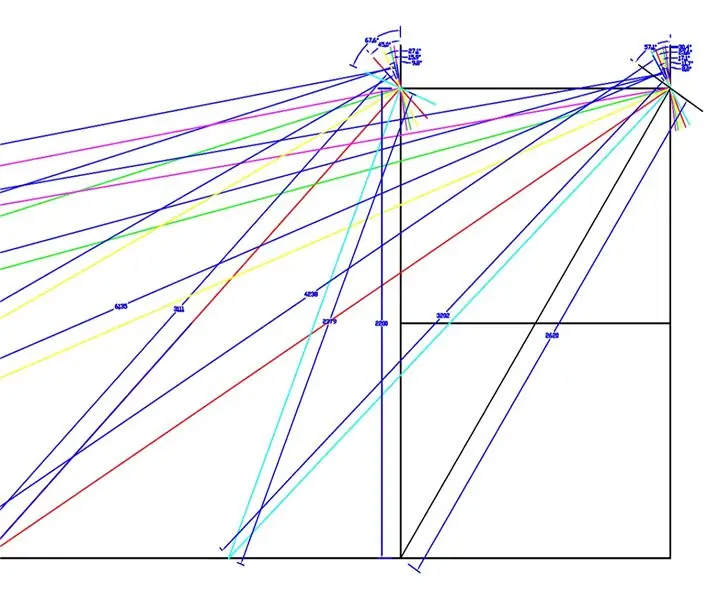
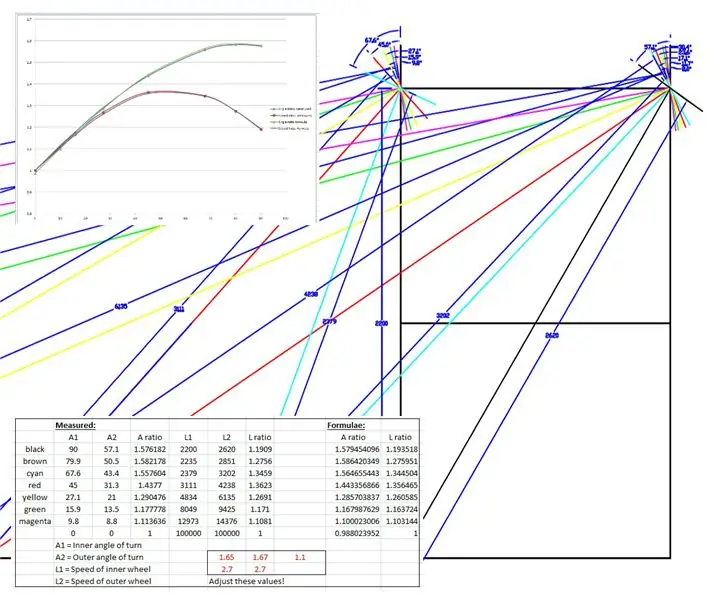
Det ble laget en fullskala tegning av WEEDINATOR forhjul og chassis med 8 forskjellige permutasjoner av innvendig hjulvinkel mellom 0 og 90 grader og de respektive svingsentrene ble kartlagt som vist på tegningene ovenfor.

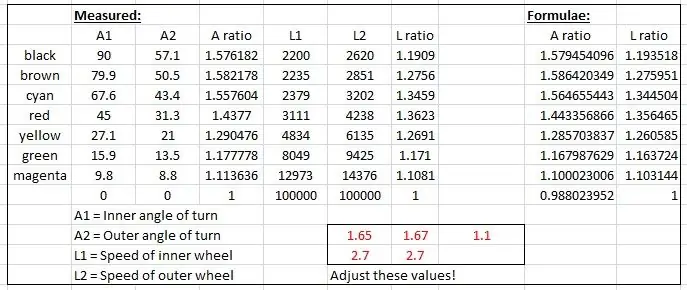
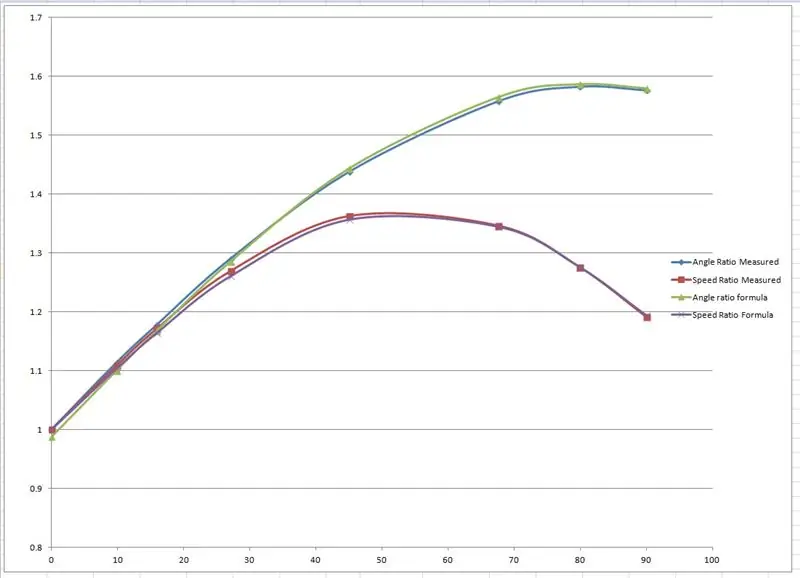
De effektive radiene ble målt fra tegningen og plottet på en graf i Microsoft Excel.

To grafer ble produsert, en av forholdet mellom venstre og høyre forhjulsaksel og en annen for forholdet mellom de to radiene for hver bestemt svingvinkel.

Jeg "fudged" opp noen formler for å etterligne de empiriske resultatene basert på en sinuskurve. En av fudgingene ser slik ut:

speedRatio = (sin (indre*1,65*pi/180) +2,7)/2,7; // indre er den indre svingvinkelen.

Kurvene ble fudged ved å endre verdiene vist i rødt i excel -filen til kurvene passet sammen.

Trinn 3: Koding av formlene

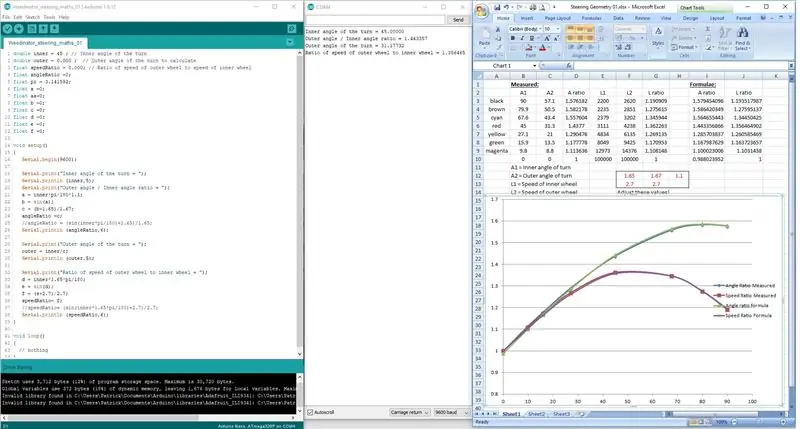
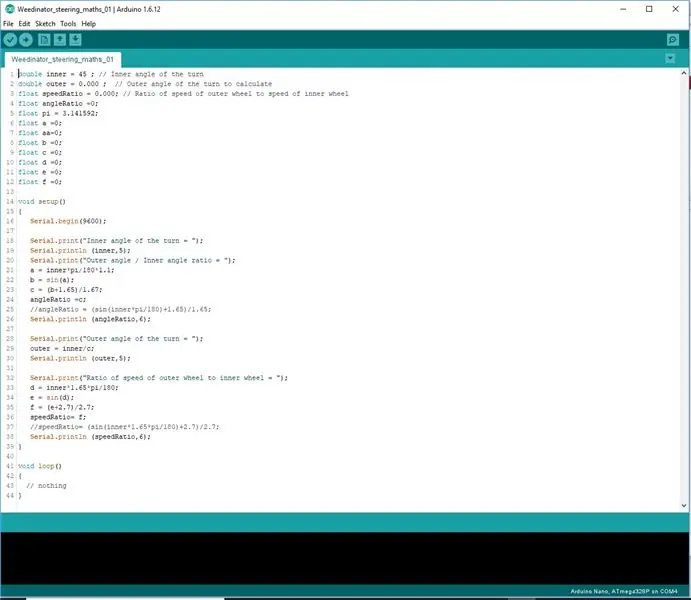
I stedet for å prøve å kode formlene på en linje, ble de delt inn i 3 stadier for å la Arduino behandle matematikken riktig.

Resultatene vises i seriell portdisplay og kontrolleres med de målte resultatene på skalategningen.