Vet du om ESP32 ADC -justering ?: 29 trinn

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-30 11:23

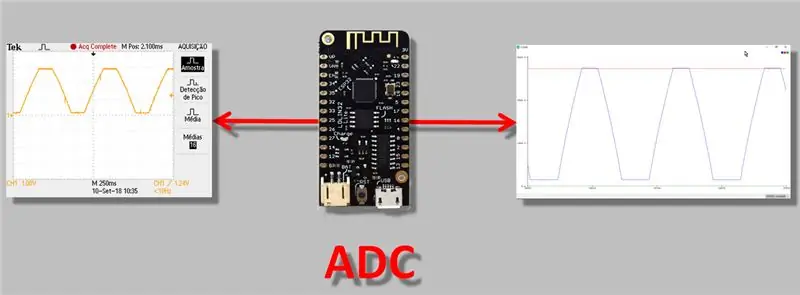
I dag skal jeg snakke om et mer teknisk problem, men en jeg tror alle som jobber med ESP32 burde vite: problemet med ADC (analog-til-digital-omformer) lesejustering. Jeg synes dette er viktig, fordi når du gjør en "måling", spesielt med et instrument som har en analog utgang, må du være helt sikker på at avlesningen utføres riktig.

I videoen i dag vil vi derfor utføre målinger ved hjelp av den "analog-digitale omformeren" til ESP32, observere konverteringsavvikene og anvende en ADC-justerings- / kalibreringsmetode.

Trinn 1: Hva er en AD -omformer?

En AD -omformer er en krets som er i stand til å oversette en analog (kontinuerlig) mengde til digitale (diskrete) verdier. Hva betyr det? Det betyr at selv om digitale verdier bare kan anta diskrete verdier dannet av kombinasjonen av nuller og ener, kan en analog mengde anta hvilken som helst verdi innenfor et område. For eksempel, hvis vi målte spenningen til en ideell AA -celle, kunne vi finne en verdi mellom 0V og 1,5V, siden dette er analog mengde. Utgangstilstanden til en ideell lampe må bare anta to tilstander (av eller på), som er en diskret størrelse. Siden mikrokontrollere jobber med denne diskrete logikken, trenger vi en krets som er i stand til å oversette en analog mengde til digital (eller diskret).

Trinn 2: Ressurser brukt

• Ett Lolin32 Lite -kort v1.0.0

• Et Tektronix TDS1001C -oscilloskop for fangst

• En USB -kabel for ESP32

• Et Hantek DSO4102C -oscilloskop som signalgenerator

Trinn 3: ESP32 ADC

Ifølge Espressif-data kan ESP32-brikkene vise en +/- 6% forskjell fra en brikke til en annen i de målte resultatene.

I tillegg har konverteringen IKKE et lineært svar for hvert tilgjengelig område for lesing. Espressif gir en metode for kalibrering og foreslår at brukerne implementerer andre metoder hvis de anser det nødvendig for å oppnå ønsket nøyaktighet.

Vi vil utføre en datainnsamling, og fra dette vil vi vise ADC -svarene og et eksempel på hvordan du bruker en matematisk prosess for å lese justeringen.

Det er flere (enklere eller mer komplekse) måter å utføre disse løsningene på. Det er opp til deg å vurdere det som passer best for prosjektet ditt.

Den som vises her vil ha et illustrerende formål og prøve å ta opp interessante punkter som kan observeres under justeringer.

Trinn 4: Krets brukt

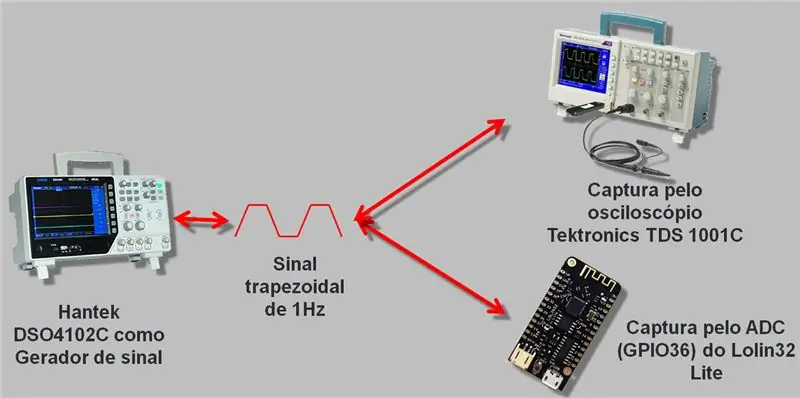
Jeg brukte et oscilloskop med en signalgenerator som går opp til 25 MHz, Hantek DSO4102C. Vi genererte en bølge som ble lest av ESP A / D og oscilloskopet. Dataene som ble samlet inn ble registrert i csv og i et regneark, som jeg vil legge igjen i slutten av artikkelen for nedlasting.

Trinn 5: Skilt brukt

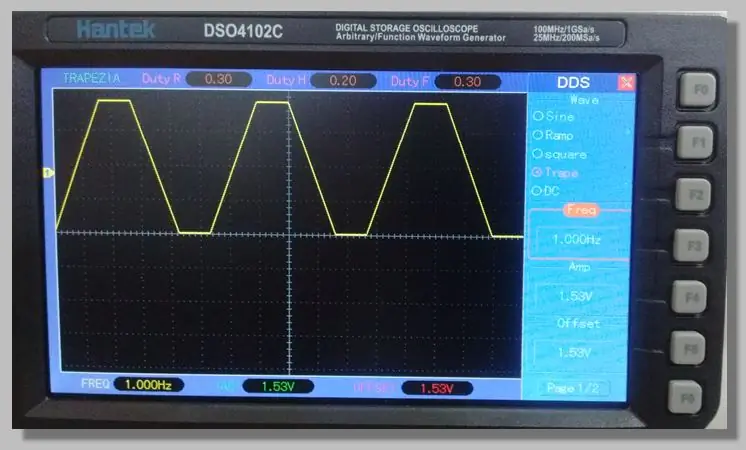
Vi valgte et lavfrekvent trapesformet signal som gir tilgang til rampene som går gjennom hele konverteringsområdet. Dette gir mulighet for et stort antall prøver på disse ramper.

Trinn 6: Data innhentet av oscilloskopet

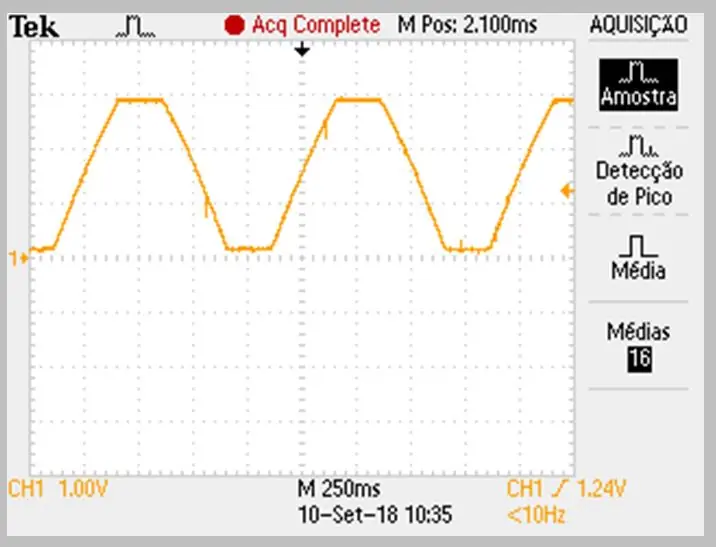
Bildet av fangsten ble utført av oscilloskopet. Dataene ble lagret i en csv -fil. Legg merke til den svake krumningen på signalets stigende og fallende ramper.

Trinn 7: Data innhentet av oscilloskopet (csv -fil i Excel)

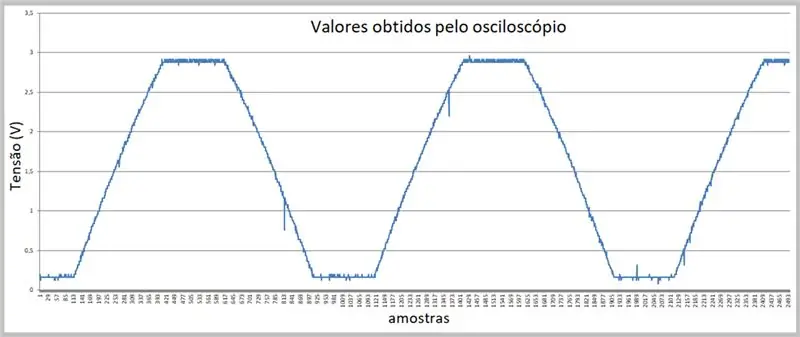
Vi har prøvetakingene her.

Trinn 8: Data innhentet av ADC

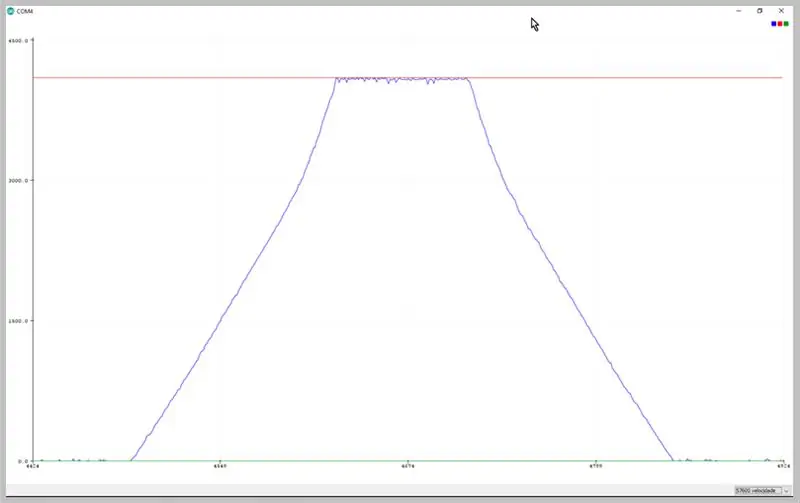
Ved å endre overføringshastigheten til serien, kan vi se dataene som er fanget opp av ADC. Observer deformasjonen av det trapesformede signalet.

Data observert på Arduino IDE seriell plotter

Trinn 9: Data innhentet av ADC - Excel

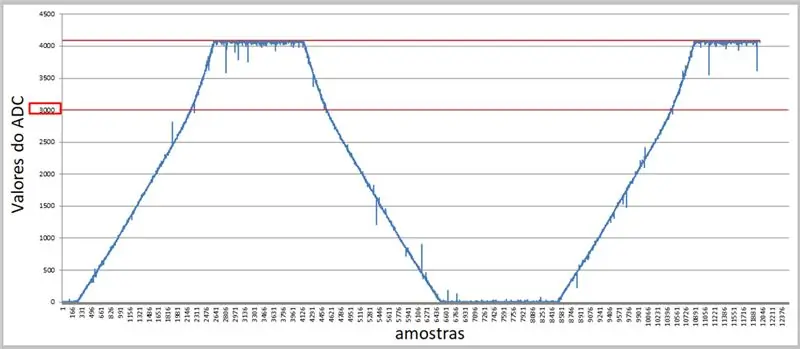
Ved å bruke en høyere hastighet og den serielle terminalen, kan vi fange opp verdiene og bruke dem i Excel for våre sammenligninger.

Trinn 10: Sammenligning av klatreramper

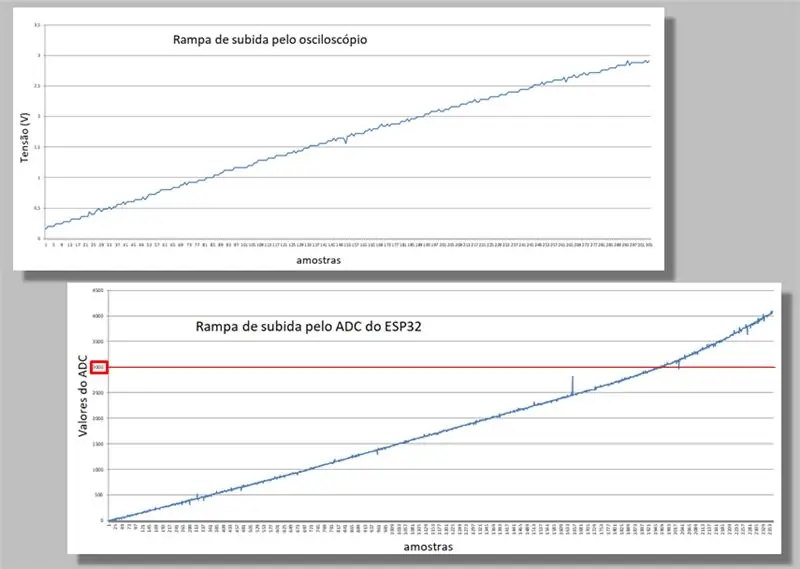
Vi sammenligner de to klatrerampene til de to fangstene.

Legg merke til krumningen som oppstår på begge ramper.

Vær også oppmerksom på at for samme rampe har vi mange flere prøver av ESP32 enn fra oscilloskopet.

Trinn 11: Likestilling av antall prøver

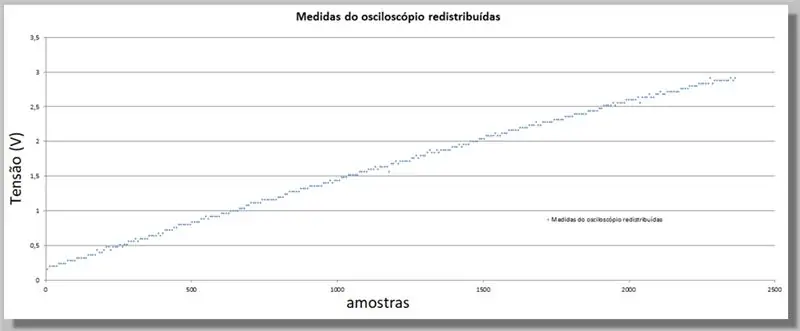
Fordi ESP32 ga et større antall prøver enn oscilloskopet, må vi likestille disse verdiene, da de vil tjene som en indeks for å sammenligne de to kurvene.

For dette vil vi gjøre en direkte sammenligning.

Vi har 305 prøver for oscilloskoprampen og 2365 prøver for ADC -rampen.

Siden ramper er i samme område, kan vi si at vi har omtrent 7,75 prøver av ADC for hvert oscilloskop.

Multiplisering av indeksen for hver oscilloskopprøve har samme kurve, men med indekser som tilsvarer ADC og de distribuerte dataene.

For å fylle ut de manglende dataene for de nye posisjonene, bruker vi en kurve som statistisk passer til de kjente dataene.

Trinn 12: Fylle hullene - trendlinjen

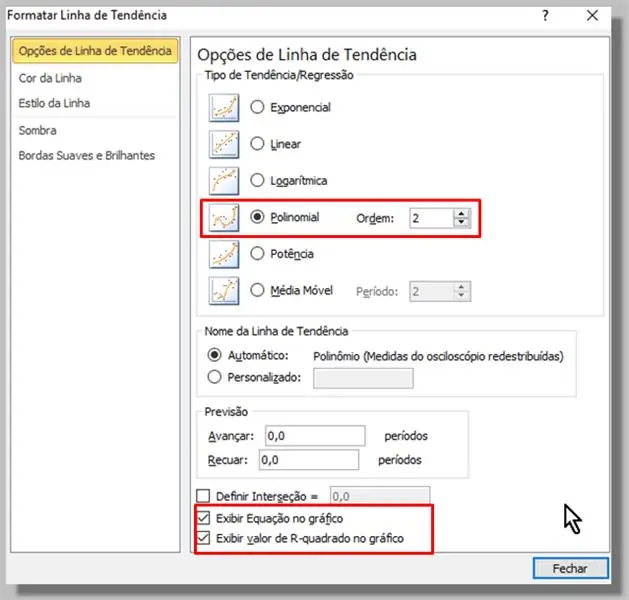
Velg de kjente dataene (blå prikker), ved å klikke og deretter klikke med høyre knapp, velger vi: "Legg til trendlinje …"

I vinduet som vises, velger vi polynomtypen (rekkefølge 2 vil være nok).

Vi sjekket også alternativene "Vis ligning i diagrammet" og "Vis verdi for R-kvadrat i diagrammet".

Vi klikker "Lukk".

Trinn 13: Fyll ut hullene - grad 2 polynomkurve

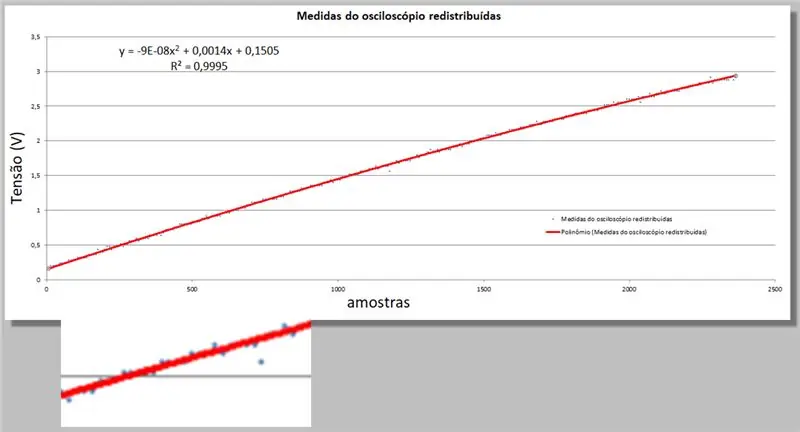
Excel gir oss to nye opplysninger; andreordens ligning som passer best til dataene, og R-kvadrat-ligningen som kvantifiserer denne tilstrekkeligheten.

Bare husk at jo nærmere 1, jo mer passende er ligningen.

La oss ikke fordype oss i matematikken som er involvert, la oss bare bruke den som et verktøy.

Trinn 14: Fylle hullene - Evaluering av funksjonen

La oss fylle ut samplingsgapene med dataene som genereres av ligningen. Og sammenligne dem punkt for punkt.

y = -9E -08x2 + 0, 0014x + 0, 1505

R² = 0, 9999

Oscilloskopspenning = -9E -08 * indeks2 + 0, 0014 * indeks + 0, 1505

Trinn 15: Konvertering av oscilloskopspenningen til en tilsvarende verdi for å sammenligne med ADC

La oss dra nytte av dette for også å transformere verdien av oscilloskopspenningen til en ekvivalent ADC -verdi.

Siden den høyeste verdien som ble oppnådd i ADP for ESP32 var 4095, som tilsvarer avlesningen på 2,958V for den samme indeksen, kan vi si at:

Hver volt i målingene av oscilloskopet tilsvarer omtrent 1384,4 enheter av AD. Derfor kan vi multiplisere alle målinger av oscilloskopet med denne verdien.

Trinn 16: Sammenligning av de to rampene som er oppnådd

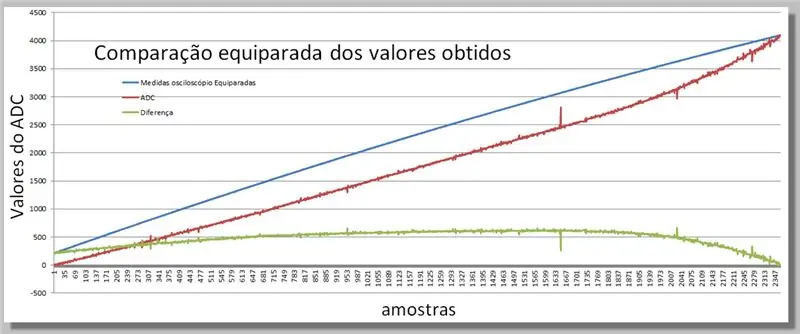
Visualisere forskjellene oppnådd i de to avlesningene.

Trinn 17: Oppførsel av ADC -leseforskjellen (ERROR)

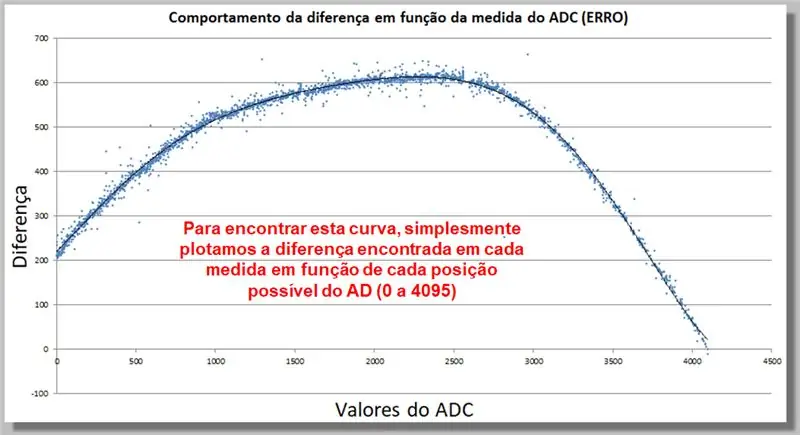
Kurven nedenfor viser hvordan forskjellen i ADC -avlesningen oppfører seg som en funksjon av målingen. Denne innsamlingen av data lar oss finne en korreksjonsfunksjon.

For å finne denne kurven, plotter vi ganske enkelt forskjellen som finnes i hvert mål som en funksjon av hver mulig AD -posisjon (0 til 4095).

Trinn 18: ADC -leseforskjellsadferd - Finne en korreksjonsfunksjon

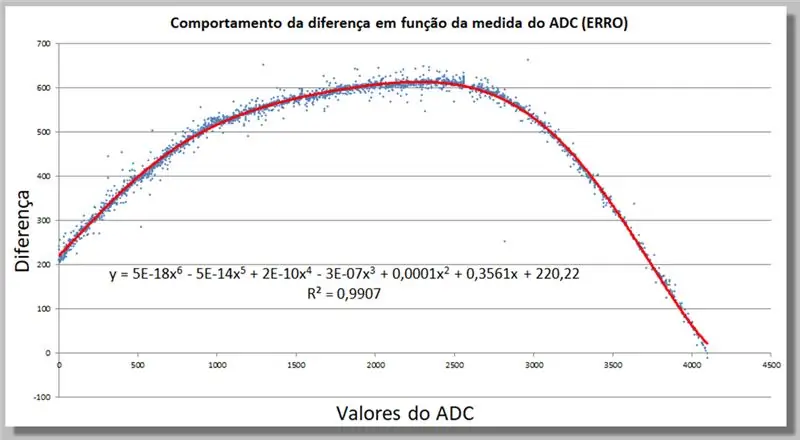
Vi kan bestemme en korreksjonsfunksjon i Excel ved å legge til en trendlinje, nå av høyere grad, til den passer tilstrekkelig med dataene våre.

Trinn 19: Bruke annen programvare

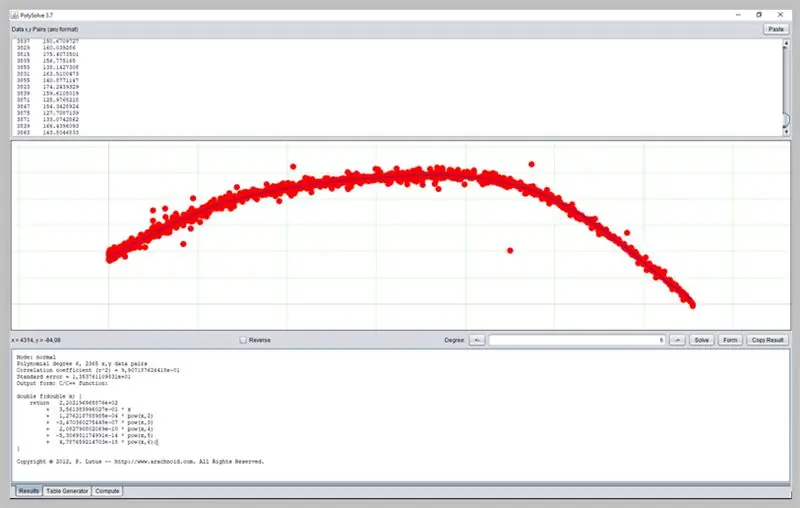
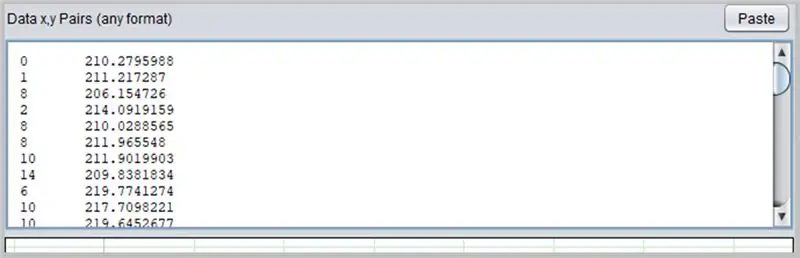
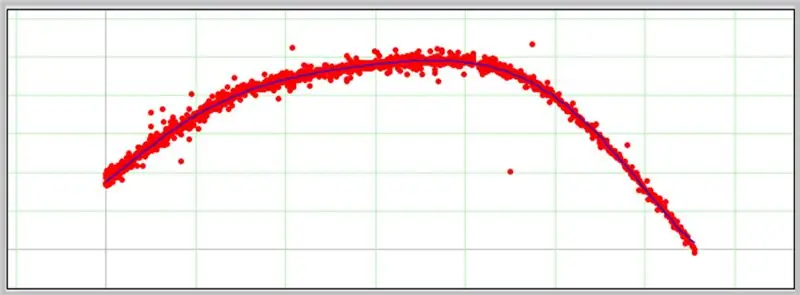
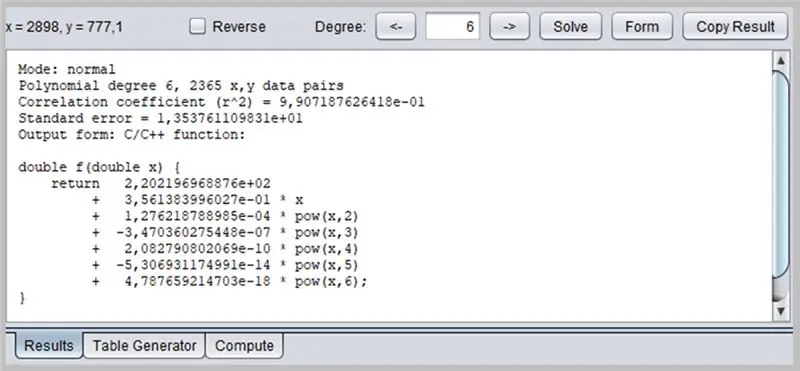
Annen interessant programvare for å bestemme kurver er PolySolve, som kan brukes direkte på lenken: https://arachnoid.com/polysolve/ eller lastes ned som et Java -program.

Den tillater anvendelse av høyere grad polynomregresjoner og levering av den formaterte funksjonen, så vel som andre funksjoner.

For å bruke det, bare skriv inn dataene i den første tekstboksen. Dataene må følge rekkefølgen X, Y atskilt med komma eller fane. Vær forsiktig når du bruker prikken korrekt som et desimaltegn.

Et diagram vil vises i den neste boksen hvis de angitte dataene er riktig formatert.

Slik gikk ADC -feilkurven vår.

Dette vinduet vil vise resultatet av regresjonen, inkludert funksjonstilstrekkelsesdata, som igjen kan ha utdataene formatert på flere måter: som en C / C ++ - funksjon, en liste over koeffisienter, en funksjon skrevet i Java, etc.

Merk: Vær oppmerksom på desimalskilletegn

Trinn 20: Konstanter og oppsett ()

Jeg påpeker her GPIO som brukes til analog fangst. Jeg initialiserer den serielle porten, så vel som pinnen som er bestemt for analog fangst.

const int pin_leitura = 36; // GPIO usado para captura analógica void setup () {Serial.begin (1000000); // Iniciciando a porta serial somente for debug pinMode (pin_leitura, INPUT); // Pino utilizado para captura analógica}

Trinn 21: Loop () og korrigeringsfunksjonen

Vi registrerer den justerte spenningen, og vi skriver ut verdiene med eller uten de riktige korreksjonene.

void loop () {int valor_analogico = analogRead (pin_leitura); // realiza a captura da tensão ajustada //Serial.print(valor_analogico + f (valor_analogico)); // imprime os valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimime os valores para debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Serial.println (0); // cria uma linha para marcar o valor mínimo de 0}

Legg merke til på linje 12 at vi har muligheten til å skrive ut dataene med tillegg av differensfunksjonen f (analog_verdi).

Trinn 22: Bruke PolySolve Correction -funksjonen

Her bruker vi PolySolve -funksjonen inne i Arduino IDE.

/* Modus: normal polynomgrad 6, 2365 x, y datapar Korrelasjonskoeffisient (r^2) = 9, 907187626418e-01 Standardfeil = 1, 353761109831e+01 Utmatingsskjema: C/C ++-funksjon: Copyright © 2012, P. Lutus - https://www.arachnoid.com. Alle rettigheter forbeholdt. */ dobbelt f (dobbelt x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Legg merke til komma-for-prikk-endringen som desimalseparator.

Trinn 23: Capture With Correction - Plotter Serial

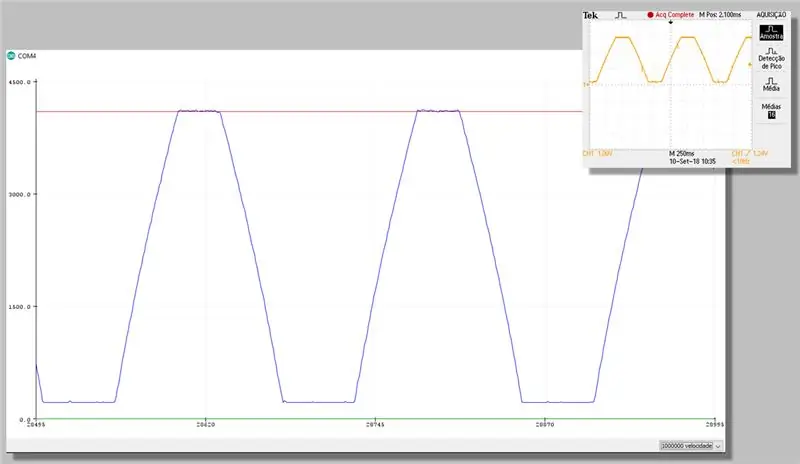
Trinn 24: Beregningskostnad

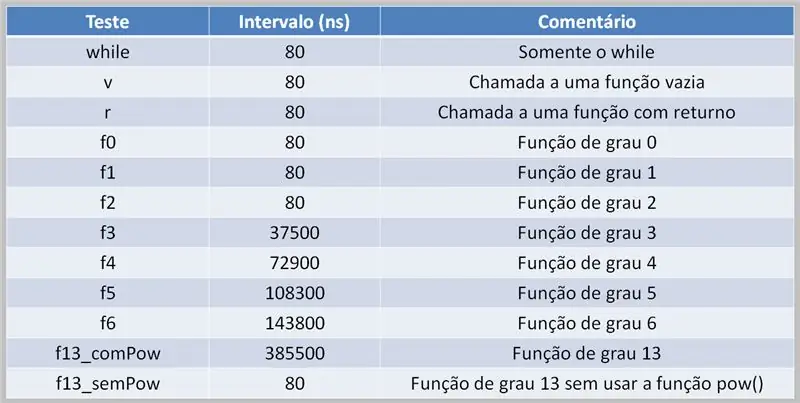
For å utføre polynomberegninger er det nødvendig for prosessoren å håndtere denne oppgaven. Dette kan føre til forsinkelser i utførelsen, avhengig av kildekoden og tilgjengelig datakraft.

Her ser vi en resultattabell for en test som bruker flergradige polynomer. Legg merke til forskjellen mellom tidspunktene da pow () -funksjonen ble brukt og når den ikke var det.

Trinn 25: Testkode - Oppsett () og Loop Start ()

Her har vi koden som ble brukt i testen vår.

ugyldig oppsett () {Serial.begin (1000000); // Iniciando a porta serial somente para debug} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000.0; // quantidade de chamadas float contador = 0,0; // contador de chamadas

Trinn 26: Testkode - sløyfe () og behandling

Jeg brukte funksjonen micros () for å få verdien i mikrosekunder.

// ============== inicia o processo float agora = micros (); // marca o instante inicial while (contador <quantidade) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a função POW contador ++; } agora = (micros () - agora) / quantidade; // determina o intervalo que se passou para cada iteração // ============== finaliza o processo

Trinn 27: Testkode - Loop () - Resultater

Vi skriver ut verdien som er returnert fra klasse 13 -funksjonen med og uten POW for sammenligning, samt behandlingsintervallet.

// imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função POW Serial.print (" -"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM a função POW Serial.print (" -"); // imprime o intervalo do processamento Serial.println (agora, 6); }

Trinn 28: Testkode - brukte funksjoner

Tomme funksjoner (bare med retur) av grad 0 og 1.

// FUNÇÃO VAZIDobbel v (dobbel x) {} // FUNÇÃO SOMENTE COM RETORNO dobbel r (dobbel x) {retur x; } // FUNÇÃO DE GRAU 0 dobbel f0 (dobbel x) {retur 2.202196968876e+02; } // FUNÇÃO DE GRAU 1 dobbel f1 (dobbel x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x; }

Grad 2, 3 og 4 funksjoner.

// FUNÇÃO DE GRAU 2dobbel f2 (dobbel x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 doble f3 (dobbel x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3); } // FUNÇÃO DE GRAU 4 doble f4 (dobbel x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2,082790802069e-10 * pow (x, 4); }

Funksjoner i klasse 5 og 6.

// FUNÇÃO DE GRAU 5dobbel f5 (dobbel x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5); } // FUNÇÃO DE GRAU 6 doble f6 (dobbel x) {retur 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Klasse 13 -funksjon ved bruk av POW.

// FUNÇÃO DE GRAU 13 USANDO O POWdobbel f13_comPow (dobbel x) {retur 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }

Grade 13 funksjon uten bruk av POW.

// FUNÇÃO DE GRAU SEM USAR O POWdobbel f13_semPow (dobbel x) {retur 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e -35 * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x; }

Trinn 29: Filer

Last ned filene:

PDF

INO

Regneark