CNC trommelplotter: 13 trinn (med bilder)

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-30 11:23

Denne instruksjonen beskriver en A4/A3 plotter laget av en seksjon av plastrør, to BYJ-48 trinnmotorer og en SG-90 servo. I hovedsak er det en flat-bed plotter rullet opp i en trommel.

Den ene motoren roterer trommelen mens den andre flytter skrivehodet. Servoen brukes til å heve og senke pennen.

Denne plotteren har en rekke fordeler fremfor en tradisjonell flatbed -plotter:

• vesentlig mindre fotavtrykk
• krever bare en lineær føringsskinne
• enkel å konstruere
• billig

En innebygd tolk godtar gcode-utgangen fra Inkscape.

Kommunikasjon med plotteren skjer via en bluetooth -lenke.

Plotteren er kompatibel med CNC-grafikk-nettbrettet beskrevet i min instruerbare

Selv om det ikke er et presisjonsinstrument, er nøyaktigheten til denne plotteren tilfredsstillende for det tiltenkte formålet å overføre akvarellkonturer til papir.

Trinn 1: Kretsen

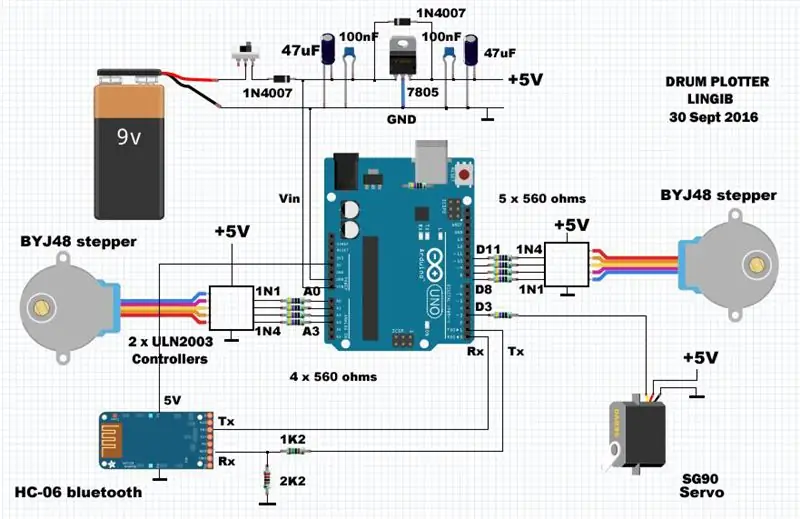
Kretsen består av en Arduino UNO R3 mikrokontroller og et tilpasset skjold som de diskrete komponentene er montert på. Strøm tilføres via en ekstern 5 volt 1 amp regulator. Gjennomsnittlig strøm er rundt 500mA.

BYJ-48 trinnmotorer er festet til PORTB (pinner D8, D9, D10, D11) og PORTC (pinner A0, A1, A2, A3). SG-90 pennløfteservo er festet til pinne D3.

Motstandene på 560 ohm, som kan utelates, gir et mål for kortslutningsbeskyttelse for arduinoen hvis noe skulle gå galt. De gjør det også lettere å koble skjoldet når de fungerer som "hoppere" over tilførselsskinnene.

Motstandene 1k2 og 2K2 forhindrer skade på HC-06 bluetooth-modulen [1] ved å slippe 5 volt utgangen fra arduinoen ned til 3,3 volt.

[1] Koble fra HC-06 bluetooth-modulen når du laster opp kode til arduinoen via USB-porten. Dette vil unngå konflikter i seriell port.

Trinn 2: Den lineære stasjonen

Den lineære drivenheten er laget av en lengde på 3 mm x 32 mm aluminiumstang, en stripe av aluminiumsplate og fire små kulelager.

Aluminium er tilgjengelig fra de fleste maskinvarebutikker. U624ZZ 4x13x7mm U-sporskiver er tilgjengelig fra

Enkle håndverktøy er alt du trenger. Skjær aluminiumsstangen slik at den passer til plotterens dimensjoner.

Motorenheten

Monter BJY-48 trinnmotor gjennom stangen i den ene enden og fest en GT2 20 tann, 5 mm boring, remskive til motorakselen. Monter nå en annen GT2 -remskive i den andre enden av stangen slik at remskiven kan rotere fritt. Jeg brukte en 5 mm diameter rørformet (radio) avstandsstykke og en 3 mm bolt for å oppnå dette.

Sløyfe nå en lengde med GT2 -tannrem rundt remskivene. Fest tannreimens ender med en halvvridning slik at tennene fletter seg sammen og festes med en kabelbinder.

Fest til slutt vognen til tannremmen med et kabelbinder.

Vognenheten

Vognenheten er laget av en stripe av aluminiumsplate [1] som U624ZZ -remskivene er boltet på. Bruk om nødvendig en 4 mm skive for å plassere remskivene fra aluminiumsplaten.

Remskivene, som har et 4 mm spor, strekker seg over aluminiumstangen topp og bunn slik at det ikke er noen vertikal bevegelse, men aluminiumslisten beveger seg fritt til venstre og høyre.

For å sikre at vognen går fritt, må du først montere de to øverste remskivene og deretter markere posisjonene til de to nederste trinsene med remskivene sittende på stangen. Hullene til disse to trinsene kan nå bores. Bruk en liten "pilot" -bor først for å forhindre at den større 4 mm boren driver.

Før du bøyer aluminiumstrimmelen til et "U", borer du et hull på toppen og bunnen for å passe til pennens diameter. Fullfør nå svingene.

Fest tannremmen til vognen ved hjelp av et kabelbånd og en 3 mm bolt mellom de to øverste remskivene.

Pennløfterenheten

Fest en SG-90-servo på toppen av vognenheten med ett eller to kabelbånd.

Slipp pennen nedover de to hullene du har boret. Sørg for at pennen glir opp og ned fritt.

Fest en "krage" til pennen slik at pennen er rett unna trommelen når servoen er i oppposisjonen.

[1] Aluminium kan kuttes ved å slå begge sider av arket med en skarp kniv (boksekutter) og deretter bøye snittet over kanten på et bord. Noen vrikker og arket vil bryte og etterlate et rett brudd. I motsetning til tinn-snips knekker denne metoden ikke aluminiumet.

Trinn 3: Trommelen

Trommelen består av en seksjon av plastrør med to endepropper [1].

Bruk et kompass, innstilt på den innvendige radius av røret ditt, for å tegne kontakten på endepluggen. Klipp nå rundt hver kontur med en fin bladsag ("coping", "fret"), og tilpass deretter hver endeplugg ved hjelp av en trerasp. Fest endepluggene med små skruer som er senket ned.

En 6 mm konstruksjonsbolt gjennom midten av hver endeplugg danner akselen.

Trommeldimensjoner

Trommeldimensjonene bestemmes av papirstørrelsen. En trommeldiameter på 100 mm støtter A4 -portrett og A3 -landskap. En trommeldiameter på 80 mm støtter bare A4 -landskap. Bruk så liten trommeldiameter som mulig for å redusere tregheten … BYJ-48-motorene er bare små.

En trommeldiameter på 90 mm er ideell for A4 -portrett- og A3 -liggende papir, ettersom de motsatte kantene, når de vikles rundt trommelen, overlapper omtrent 10 mm, noe som betyr at du bare har en søm å tape på plass.

Roter trommelen

Hver aksel passerer gjennom en aluminiumsbrakett slik at trommelen kan rotere fritt. Endeflåten forhindres ved hjelp av en GT-2, 20 tenner, 6 mm boring, remskive festet til akselen i den ene enden. Et kontinuerlig GT-2-tannrem binder BJY-48-trinnmotoren til trommelen. Motoren krever en remskive med en borestørrelse på 5 mm.

[1] Plastende plugger er tilgjengelige for de fleste rørdiametre, men ble avvist da de passet over røret i stedet for innvendig og plasten har en tendens til å bøyes. De ville sannsynligvis være greit hvis en kontinuerlig aksel ble brukt i stedet for boltene … men da trenger du en metode for å feste akselen til endepluggene.

Trinn 4: Konstruksjonstips

Sørg for at pennen beveger seg langs midten av trommelen. Dette kan oppnås ved å kutte hjørnene ut av trestøttene. Hvis pennen er utenfor midten vil den ha en tendens til å gli ned langs siden av trommelen.

Nøyaktig boring av de to pennhullene er viktig. Enhver vingling i pennestyret eller vognenheten vil forårsake vakling langs X-aksen.

Ikke stram GT-2-reimene for mye … de trenger bare å være stramme. BYJ-48 trinnmotorer har ikke mye dreiemoment.

BJY-48-trinnmotorer viser ofte små mengder tilbakeslag som er ubetydelig langs X-aksen, men er bekymringsfull når det gjelder Y-aksen. Grunnen til dette er at en rotasjon av Y-aksemotoren tilsvarer en rotasjon av trommelen, mens pennevognen krever mange svinger av X-aksemotoren for å krysse trommelens lengde. Eventuell Y-akses tilbakeslag kan elimineres ved å holde et konstant dreiemoment på trommelen. En enkel metode er å feste en liten vekt til en nylonsnor som er viklet rundt trommelen.

Trinn 5: Bresenhams linjetegningsalgoritme

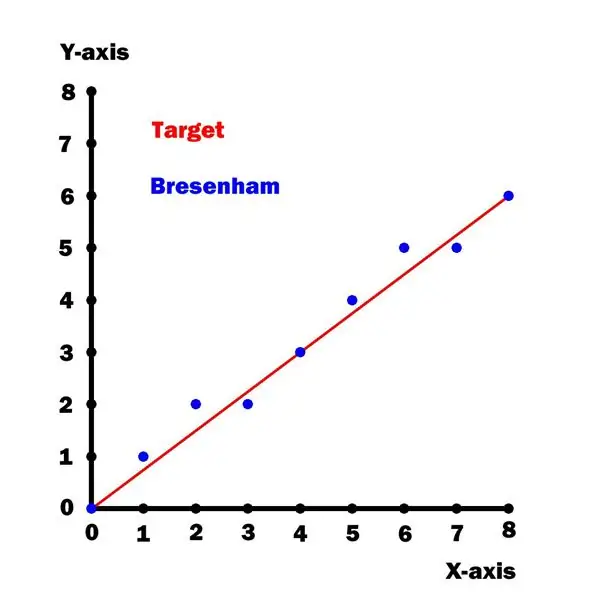
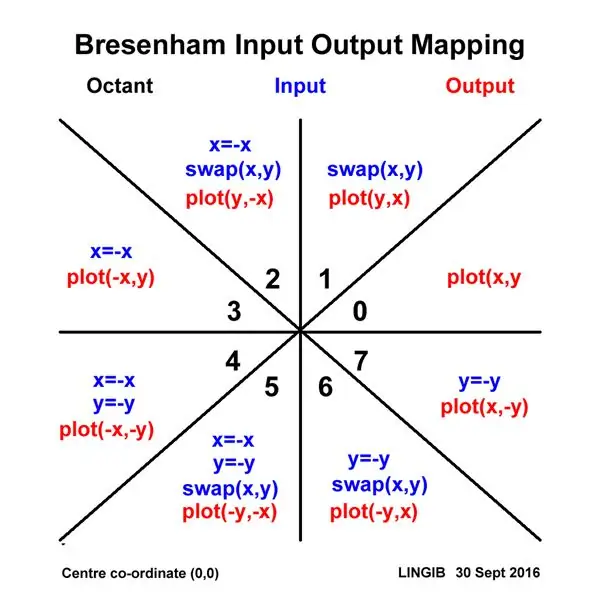
Denne plotteren bruker en optimalisert versjon [1] av Bresenhams linjetegningsalgoritme. Dessverre er denne algoritmen bare gyldig for linjebakker mindre enn eller lik 45 grader (dvs. en oktant av en sirkel).

For å omgå denne begrensningen "kartlegger" jeg alle XY -innganger til den første "oktanten", og deretter "fjerner du kartleggingen" av dem når det er på tide å plotte. Inngangs- og utgangskartfunksjonene for å oppnå dette er vist i diagrammet ovenfor.

Avledning

Resten av dette trinnet kan utelates hvis du er kjent med Bresenhams algoritme.

La oss tegne en linje fra (0, 0) til (x1, y1) der:

• x1 = 8 = horisontal avstand
• y1 = 6 = vertikal avstand

Ligningen for en rett linje som går gjennom opprinnelsen (0, 0) er gitt av ligningen y = m*x hvor:

m = y1/x1 = 6/8 = 0,75 = skråning

Enkel algoritme

En enkel algoritme for å plotte denne linjen er:

• int x1 = 8;
• int y1 = 6;
• flyte m = y1/x1;
• tomt (0, 0);
• for (int x = 1; x <= x1; x ++) {
• int y = rund (m*x);
• plott (x, y);
• }

Tabell 1: Enkel algoritme

x	m	m*x	y
0	0.75	0	0
1	0.75	0.75	1
2	0.75	1.5	2
3	0.75	2.25	2
4	0.75	3	3
5	0.75	3.75	4
6	0.75	4.5	5
7	0.75	5.25	5
8	0.75	6	6

Det er to problemer med denne enkle algoritmen:

• hovedløkken inneholder en multiplikasjon som er treg
• den bruker flytende tall som også er treg

En graf over y mot x for denne linjen er vist ovenfor.

Bresenhams algoritme

Bresenham introduserte begrepet et feilbegrep 'e' som initialiseres til null. Han innså at m*x -verdiene vist i tabell 1 kan oppnås ved påfølgende tilsetning av 'm' til 'e'. Han innså videre at y bare økes hvis brøkdelen av m*x er større enn 0,5. For å holde sammenligningen innenfor området 0 <= 0,5 <= 1 trekker han 1 fra 'e' når y økes.

• int x1 = 8;
• int y1 = 6;
• flyte m = y1/x1;
• int y = 0;
• flyte e = 0;
• tomt (0, 0);
• for (int x = 1; x <= x1; x ++) {
• e+= m;
• hvis (e> = 0,5) {
• e -= 1;
• y ++;
• }
• plott (x, y);
• }

Tabell 2: Bresenhams algoritme

x	m	e	e-1	y
0	0.75	0	0	0
1	0.75	0.75	-0.25	1
2	0.75	0.5	-0.5	2
3	0.75	0.25		2
4	0.75	1	0	3
5	0.75	0.75	-0.25	4
6	0.75	0.5	-0.5	5
7	0.75	0.25		5
8	0.75	1	0	6

Hvis du undersøker algoritmen og tabell 2, vil du se at;

• hovedsløyfen bruker bare addisjon og subtraksjon … det er ingen multiplikasjon
• mønsteret for y er det samme som for tabell 1.

Men vi bruker fremdeles flytende tall … la oss fikse dette.

Bresenhams (optimaliserte) algoritme

Bresenhams flytende punktalgoritme kan konverteres til et heltall hvis vi skalerer 'm' og 'e' med 2*x1, i så fall m = (y1/x1)*2*x1 = 2*y1

Bortsett fra skalering 'm' og 'e' er algoritmen lik den ovenfor bortsett fra:

• vi legger 2*y1 til 'e' hver gang vi øker 'x'
• vi øker y hvis e er lik eller større enn x1.
• vi trekker 2*x1 fra 'e' i stedet for 1
• x1 brukes til sammenligning i stedet for 0,5

Hastigheten til algoritmen kan økes ytterligere hvis løkken bruker null for testen. For å gjøre dette må vi legge til en forskyvning til feilbegrepet 'e'.

• int x1 = 8;
• int y1 = 6;
• int m = (y1 << 1); // konstant: stigning skalert med 2*x1
• int E = (x1 << 1); // konstant: 2*x1 for bruk i sløyfe
• int e = -x1; // forskyvning av -E/2: testen er nå utført på null
• tomt (0, 0);
• int y = 0;
• for (x = 1; x <= x1; x ++) {
• e += m;
• hvis (e> = x1) {
• e -= E
• y ++;
• }
• plott (x, y);
• }

Tabell 3: Bresenhams (optimaliserte) algoritme

x	m	E	e	e - E	y
0	12	16	-8		0
1	12	16	4	-12	1
2	12	16	0	-16	2
3	12	16	-4		2
4	12	16	8	-8	3
5	12	16	4	-12	4
6	12	16	0	-16	5
7	12	16	-4		5
8	12	16	8	-8	6

Nok en gang er mønsteret for y det samme som i de andre tabellene. Det er interessant å merke seg at tabell 3 bare inneholder heltall og at forholdet m/E = 12/16 = 0,75 som er linjen 'm'.

Denne algoritmen er ekstremt rask ettersom hovedløkken bare innebærer addisjon, subtraksjon og en sammenligning med null. Multiplikasjon brukes ikke bortsett fra når vi initialiserer verdiene for 'E' og 'm' ved å bruke "venstre-shift" for å doble verdiene til x1 og y1.

[1] Denne optimaliserte versjonen av Bresenhams algoritme er fra et papir "Bresenham Line and Circle Drawing", copyright © 1994-2006, W Randolph Franklin (WRF). Materialet hans kan brukes til ideell forskning og utdanning, forutsatt at du krediterer ham og lenker tilbake til hjemmesiden hans,

Trinn 6: Koden

Last ned den vedlagte filen til en mappe med samme navn, og last den deretter opp til plotteren ved hjelp av arduino IDE (integrert utviklingsmiljø).

Koble fra HC-06 bluetoorh-modulen før du prøver å laste opp. Dette er nødvendig for å unngå en seriell portkonflikt med USB -kabelen.

Tredjeparts kode

I tillegg til.ino-koden ovenfor trenger du følgende programvarepakker som er gratis / donasjonsmateriell:

• Teraterm som er tilgjengelig fra
• Inkscape som er tilgjengelig fra

Instruksjoner for installering og bruk av hver av de ovennevnte tredjepartspakkene finner du i artikkelen min

Trinn 7: Meny

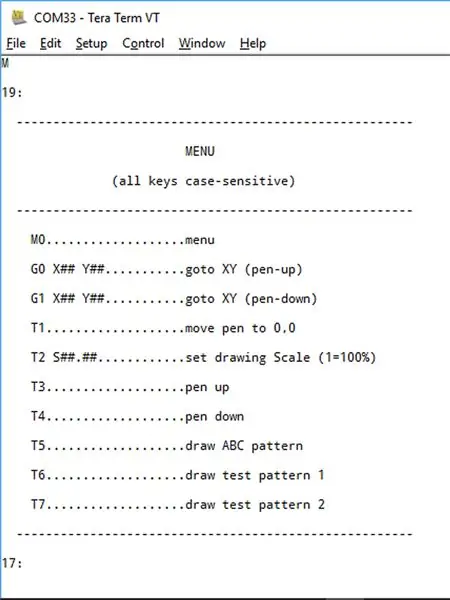
Opprett en Bluetooth -tilkobling med plotteren din ved hjelp av "Teraterm".

Slå på "caps lock" ettersom alle kommandoer er i store bokstaver.

Skriv inn bokstaven 'M', og en meny skal vises som vist ovenfor.

Menyen er rimelig selvforklarende:

• M (eller M0) viser menyen
• G0 lar deg sende pennen til en bestemt XY-koordinat med pennen hevet.
• G1 lar deg sende pennen til en bestemt XY-koordinat med pennen senket.
• T1 lar deg plassere pennen din over 0, 0-koordinaten din. Skriv 'E' for å gå ut.
• T2 lar deg skalere tegningen din. For eksempel "T2 S2.5" skalerer tegningen din til 250%. Standardskalaen er 100%
• T3 og T4 lar deg heve eller senke pennen.
• T5 tegner et "ABC" testmønster.
• T6 tegner et "mål".
• T7 tegner et sett med radielle linjer, hvis formål er å verifisere at Bresenhams algoritme fungerer i hver av de åtte "oktanter"

Merknader:

• alle pennbevegelser bruker tegneskalaen ved hjelp av menyalternativet T2
• "17:" og "19:" tallene er "Xon" og "Xoff" terminal håndtrykkskoder fra arduino -tolken.

Trinn 8: Kalibrering

Verdiene for X_STEPS_PER_MM og Y_STEPS_PER_MM er for en trommel med en diameter på 90 mm.

Verdier for andre trommeldiametere kan beregnes ved hjelp av følgende forhold:

• trommens omkrets er PI*diameter
• 2048 trinn tilsvarer en omdreining for hver motoraksel
• en omdreining av en GT-2 remskive tilsvarer 40 millimeter lineær bevegelse av et registerreim

En annen metode er å skrive inn følgende kommandoer,

• G1 X0 Y100
• G1 X100 Y100

mål deretter lengden på de resulterende linjene og "skala" verdiene for X-STEPS_PER_MM og Y_STEPS_PER_MM

Trinn 9: Gcode -forbehandling

Denne plotteren krever bare fire av Inkscape gcodes (dvs. G0, G1, G2, G3). Koden vil kjøres betydelig raskere hvis vi fjerner alle unødvendige g -koder og kommentarer.

For å gjøre dette trenger du en kopi av "Notisblokk ++". Denne gratis tekstredigereren inneholder en "vanlig uttrykk" søkemotor for å finne og fjerne uønsket tekst. Notisblokk ++ er tilgjengelig fra

Åpne filen som skal endres med Notisblokk ++ og plasser markøren øverst i filen.

Velg "Vis/Vis symbol/Alle tegn" etterfulgt av "Søk/erstatt …" fra den øverste menylinjen.

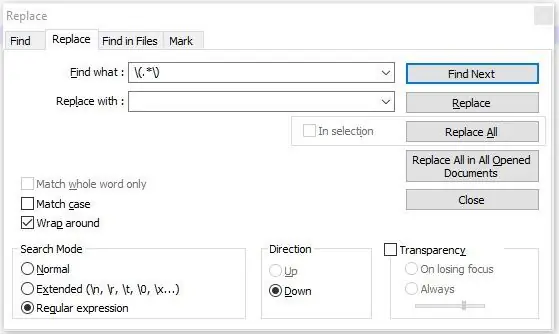
Klikk på avmerkingsboksen "Vanlig uttrykk" (se første bilde) og skriv inn hver av de følgende kodesekvensene i søkeboksen.

Klikk "Erstatt alle" etter hver oppføring:

• %
• (.*)
• ^M.*$
• Z.*$

Regeluttrykkene ovenfor fjerner alle % -symboler, alle kommentarer vist i parentes, alle M -koder, alle Z -koder og kodene som følger.

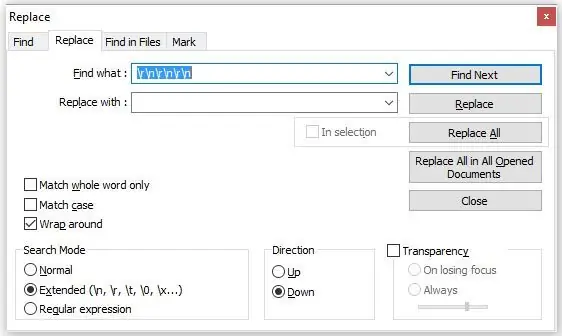
Klikk nå i avmerkingsboksen "Utvidet uttrykk" (se 2. bilde) og skriv inn følgende kodesekvens:

r / n / r / n / r / n

Dette uttrykket fjerner de uønskede vognreturene og linjefødene som er opprettet av den første sekvensen.

Lagre filen under et annet navn ved å bruke "Lagre som".

Ferdig.

Trinn 10: Resultater

Denne plotteren ble bygget som "proof of concept" og hadde aldri til hensikt å være perfekt. Når det er sagt, er ikke resultatene så ille. De oppfyller definitivt mitt designmål om å overføre akvarellkonturer til papir.

De tre første bildene er de innebygde testmønstrene henholdsvis T5, T6, T7.

"Hei verden!" mønster ble sendt til plotteren via bluetooth. En "forhåndsbehandlet" kopi av denne filen er vedlagt.

Trinn 11: Kodeoppdatering

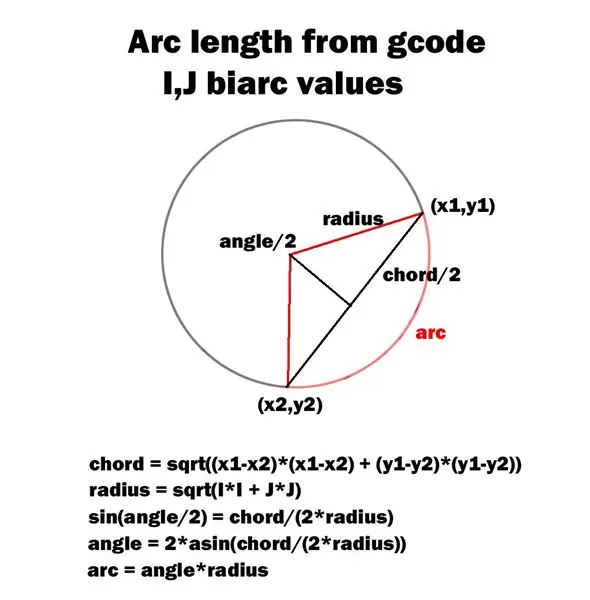
Koden for denne plotteren er oppdatert til Drum_Plotter_V2.ino.

Endringer fra den opprinnelige Drum_Plotter.ino inkluderer:

• jevnere plassering av pennen
• gjenkjenner nå G02 gcode -instruksjoner (buer med klokken)
• gjenkjenner nå G03 gcode-instruksjoner (buer mot klokken)

Det vedlagte diagrammet beskriver metoden min for å beregne buevinkelen.

Trinn 12: Drum_plotter_v3.ino

En kodeoppdatering for "CNC Drum Plotter" er vedlagt.

"drum_plotter_v3.ino" fikser en mindre feil som påvirket plotterens nøyaktighet.

Endringshistorikk

Versjon 2:

Bi-buekurver lagt til

Versjon 3:

Følgende funksjoner ble omskrevet for å løse en mindre feil som påvirket plotterens nøyaktighet.

• (int) erstattet med runde () i funksjonen move_to ().
• draw_line () funksjon "oktant" søkealgoritme forbedret
• Tolken bruker nå strengfunksjoner i stedet for tips som forenkler designet. For eksempel kan vi nå søke etter "MENY" i stedet for å lete etter bokstaven 'M', og deretter trekke ut heltallet som følger. Dette lar deg tilpasse plotteren med dine egne kommandoer.

Trinn 13: Drum_plotter_plotter_v4.ino

16. januar 2017:

Koden for denne trommelplotteren er ytterligere optimalisert. Flere funksjoner er lagt til.

Endringene inkluderer:

• raskere draw_line () algoritme
• matchende move_to () -funksjon
• trinn tellere
• mindre feilrettelse

For ytterligere detaljer, les kommentarene i "drum_plotter_v4.ino" vedlagt.

Klikk her for å se mine andre instrukser.