Rekursivt summering av en matrise i Java: 9 trinn

2025 Forfatter: John Day | [email protected]. Sist endret: 2025-01-13 06:58

Rekursjon er en veldig nyttig og tidseffektiv prosedyre som raskt kan løse et problem med svært lite kode. Rekursjon innebærer metoden du lager for å kalle seg selv for å forkorte det opprinnelige problemet.

I dette eksemplet summerer vi en rekke med 10 heltall, men størrelsen kan være av hvilken som helst lengde.

Rekvisita

Du bør kunne grunnleggende java -syntaks og ha IDE eller et tekstredigeringsprogram for å skrive koden for denne oppgaven.

Trinn 1: Konfigurer hovedmetoden din

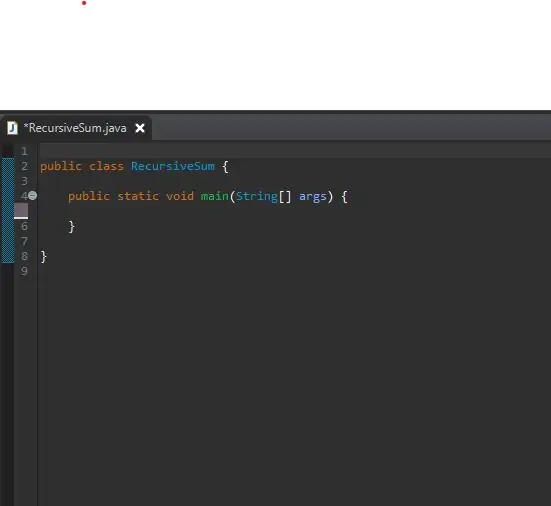
For å begynne, sett opp hovedmetoden din i en nyopprettet klasse. Jeg har kalt klassen min for RecursiveSum. Det er her du vil lage en rekke heltall og kalle din rekursive metode.

Trinn 2: Lag din rekursive metodeoverskrift

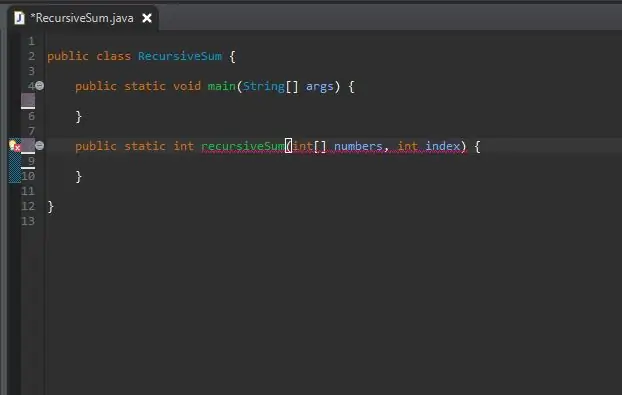
Utenfor hovedmetoden, opprett metodeoverskriften for din rekursive metode.

Metoden er statisk, da den ikke vil kreve at et objekt bruker den på.

Returtypen er int, ettersom matrisen vi skal bruke vil være full på heltall. Dette kan imidlertid endres til hvilken nummertype matrisen inneholder.

Jeg har kalt metoden min for recursiveSum som vil ta to parametere; en rekke heltall og indeksen vi skal legge til summen. Jeg har kalt disse parameterne henholdsvis tall og indeks.

Du vil se feil akkurat nå, og det er greit. De vil bli fikset senere.

Trinn 3: Lag din Kicker/base Case

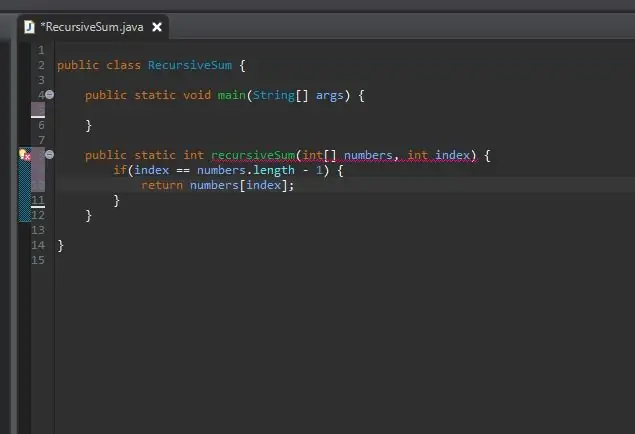
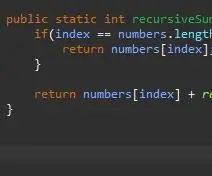
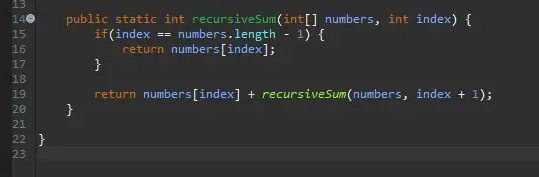
En rekursiv metode trenger en kicker/base case. Dette er tilstanden som vil stoppe metoden din fra å kalle seg uendelig. Denne basissaken kan betraktes som den mest enkle saken vi vil støte på. I dette tilfellet vil hovedtilfellet være når vi er på slutten av matrisen. Hvis den nåværende indeksen er lik lengden på matrisen (minus 1 fordi matriser begynner å telle fra 0 ikke 1), er vi på slutten, og vi returnerer bare det elementet til indeksen.

Trinn 4: Det rekursive trinnet

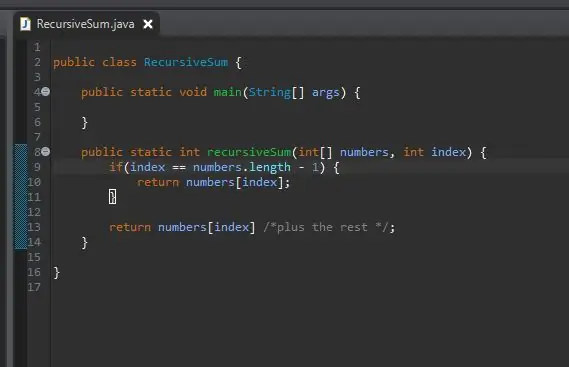
Når vi har vår basiskasse, er det neste trinnet vårt rekursive trinn. Det er her magien skjer. Vi har håndtert saken når indeksen vår er lik det siste elementet i matrisen. Hva om vi ikke er det siste elementet i matrisen vår? Hva om vi bare kunne fortelle det å legge til vårt nåværende element pluss det neste? Til slutt vil vi treffe slutten av vårt utvalg, og basissaken vår vil påvirke.

For å oppnå dette, returnerer vi ganske enkelt vår nåværende indeks og "legger til resten" av matrisen.

Trinn 5: Forkort problemet

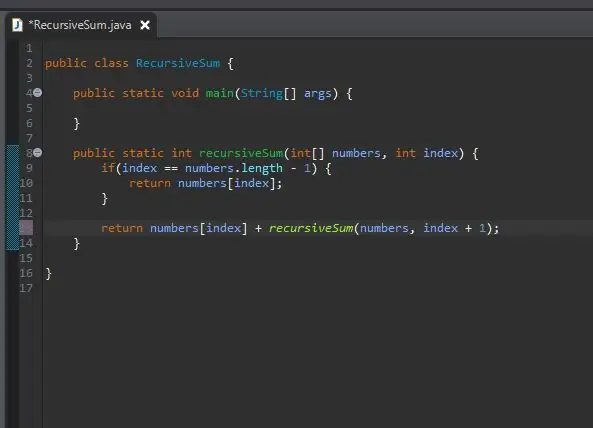
Hvordan "legger vi til resten"? Vi har allerede en metode som vil legge til et bestemt element; vår rekursiveSum () -metode! Vi kan kalle det igjen, men endre hvilken indeks vi summerer.

Vi sender i samme matrisen vi behandler, men vi sender inn den neste indeksen fra vår nåværende indeks. Vi gjør dette ved ganske enkelt å legge en til vår nåværende indeks som vist.

Trinn 6: Lag matrisen med heltall

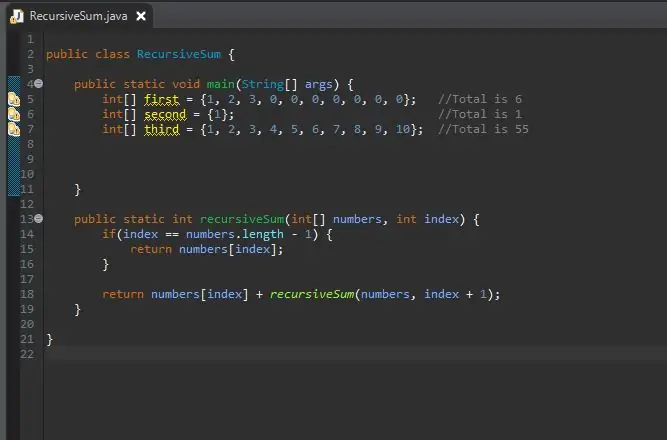
Nå som vår rekursive summeringsmetode er fullført, kan vi lage vårt utvalg som vi vil behandle. Denne matrisen vil være i vår hovedmetodeblokk.

Du kan lage størrelsen på matrisen så lenge du vil. Jeg har laget noen forskjellige matriser med forskjellige størrelser og verdier for å vise at det ikke bare fungerer på en enkelt størrelse.

Trinn 7: Ring til metoden med arraysene dine

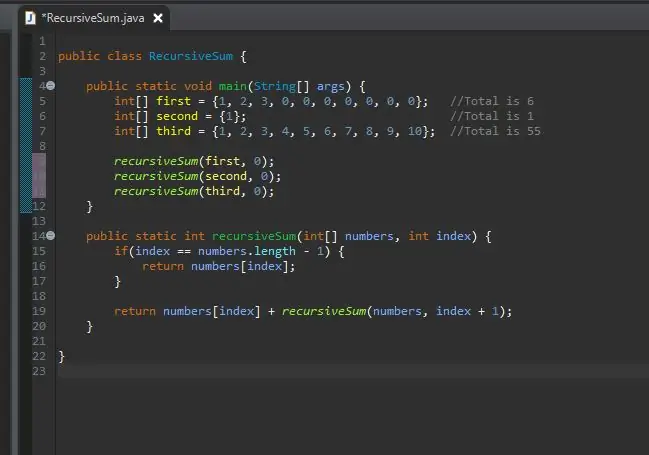
Nå kan du ringe din rekursive metode og sende disse matrisene til den. Nå kan du kjøre programmet.

Trinn 8: Skriv ut resultatene

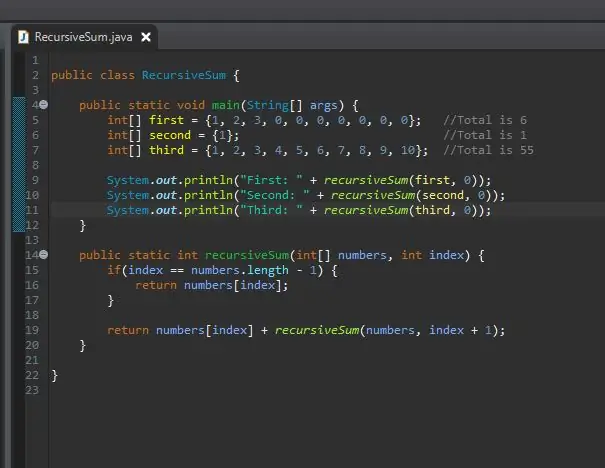
Ingenting skjedde. Hvorfor? Rekursiv sum returnerer et heltall, men vi har ikke gjort noe med dette heltallet. Det gjorde jobben sin, men vi kan ikke se resultatet. For å se resultatet, skriver vi det ut slik. Etter at du har kjørt dette, bør du se resultatene for hver av matrisene dine.

Trinn 9: Gratulerer

Du har fullført en rekursiv funksjon. Endre gjerne størrelsen på matrisene dine. Hvis du tester den, vil du legge merke til at den krasjer når du har en tom matrise. Vi har ikke redegjort for det, men det er en fin måte å forbedre din rekursive metode.