Grid Tie Inverter: 10 trinn (med bilder)

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-30 11:21

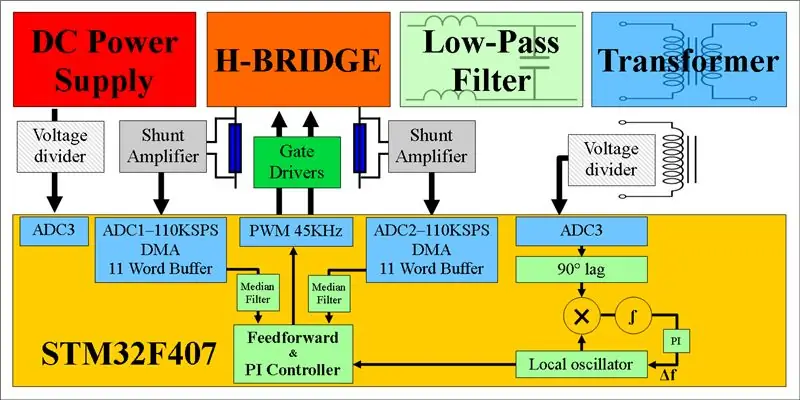
Dette er et kjøttfullt prosjekt, så fest deg!

Omformere med strømnett gjør det mulig å skyve strømmen inn i en stikkontakt, noe som er en fantastisk evne. Jeg synes kraftelektronikken og kontrollsystemene som er involvert i designen deres er interessante, så jeg bygde min egen. Denne rapporten deler det jeg lærte og dokumenterer hvordan jeg gjorde ting. Jeg vil være interessert i eventuelle kommentarer du har (bortsett fra de om ikke å rote med strømnettet).

Alle konseptene er skalerbare, men dette oppsettet hadde en maksimal effekt på 40 watt før filterinduktorene begynte å mette. Utgangsstrømmen var sinusformet med THD <5%.

Se programvaren på min GitHub

Rekvisita

• Jeg brukte utviklingsbordet STM32F407. Den kjører på 168 MHz og har 3 innebygde ADCer som kan 12bit oppløsning på over 2,4 MSPS (millioner prøver per sekund) hver. Det er sinnsykt!
• Jeg brukte utviklingsbordet DRV8301. Dette huser en 60v H-bro sammen med de nødvendige portdriverne, nåværende shuntene og strømforsterkere. Super snill!
• Jeg brukte en toroidformet transformator på 230-25v med 2 utgangskraner. Dette betydde at jeg ikke måtte produsere nettspenning direkte, men kunne jobbe med toppspenninger på 40 volt i stedet. Mye tryggere!
• Jeg koblet en mengde induktorer og kondensatorer sammen for å få L- og C -verdiene jeg ønsket for filteret.
• Et oscilloskop og differensialprobe er nøkkelen for et prosjekt som dette. Jeg har et Picoscope

Trinn 1: Hva er strømnettet?

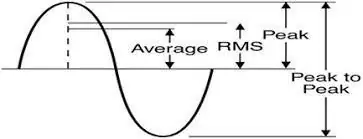
Det du får ved en stikkontakt (i Storbritannia) er et 50Hz 230v RMS sinusformet signal med en veldig lav impedans. Noen ting å si om det:

50Hz - Nettfrekvensen opprettholdes veldig nøyaktig ved 50Hz. Det varierer litt, men 90% av tiden er det mellom 49,9-50,1Hz. Se her. Du kan forestille deg at alle de enorme generatorene i kraftstasjoner opp og ned i landet snurrer i kor. De roterer synkront og produserer for oss et 50Hz sinusformet signal. Deres kombinerte massive rotasjons treghet tar tid å bremse eller øke hastigheten.

I teorien, hvis det ble festet en ENORM belastning til nettet, ville det begynne å bremse landets generatorer. Men som svar ville gutta på National Grids kontrollkontor be kraftstasjoner om å steke kjelene sine, skru opp varmen og tvinge generatorene vanskeligere til å følge med etterspørselen. Således er tilbud og etterspørsel i en kontinuerlig dans med hverandre.

En ting å si om 50Hz -signalet. Selv om det varierer veldig omtrent 50Hz, sørger gutta på toppen for at gjennomsnittsfrekvensen over dagen er nøyaktig 50Hz. Så hvis nettet er på 49,95Hz i 10 minutter, sørger de for at det går på 50,05Hz senere for å bringe det eksakte antallet sykluser til 50Hz x 60sekunder x 60minutter x 24 timer = 4, 320, 000/dag. De gjør dette nettopp ved å bruke International Atomic Time. Husholdnings-, kontor- og industriapparater kan derfor bruke nettfrekvensen til å holde tiden. Dette gjøres vanligvis med for eksempel mekaniske stikkontakter.

230v - Dette er RMS (Root Mean Square) spenningen til 50Hz -signalet. Selve signalet svinger opp til en 325v topp. Dette er viktig å vite, for hvis du bygger en omformer må du produsere så høye spenninger hvis du skal få strøm til å strømme inn i pluggene.

I virkeligheten er spenningene sett ved en plugg i huset ditt ganske varierende. Det skyldes spenningsfall over motstanden i ledninger, kontakter, sikringer, transformatorer etc. Det er motstand overalt. Hvis du slår på en elektrisk dusj som drar 11 kilowatt (det er ~ 50Am), vil selv 0,2 ohm motstand gi deg 10 volt. Du kan se dette som at lysene blir litt svakere. Store motorer, for eksempel de i hoover, trekker enorme strømmer mens motoren får fart. Så du ser ofte en liten flimmer av lysene når du slår dem på.

Poenget mitt er at nettspenningen er mye mer variabel. Her i Storbritannia skal det være 230v med en +10%/-6% toleranse. Du kan forvente å se plutselige endringer og svingninger når store belastninger i nærheten slås av/på. Tenk på tørketrommel, vannkoker, ovn, hoover osv.

Sinusformet - Signalet skal være en fin ren sinusbølge, men i virkeligheten suger noen ikke -lineære apparater kraften sin fra visse punkter i sinusbølgesyklusen. Dette introduserer forvrengning, og derfor er signalet ikke en perfekt sinusbølge. Ikke -lineære belastninger inkluderer vanligvis datamaskinens strømforsyninger, lysrør, ladere, TVer, etc.

Total harmonisk forvrengning (THD) kvantifiserer dette i bølgeformen. Det er forskrifter for hvor ren en omformers utgang må være. Hvis det ikke er i stand til å produsere et rent nok signal, blir det ikke godkjent for salg. Dette er viktig fordi harmonisk innhold i nettet reduserer effektiviteten til noen enheter som er koblet til det (spesielt merkelige harmoniske). Jeg tror maks tillatt THD er 8%

Lav impedans - Når du tenker på en grid tie inverter, vil dette være viktig å vurdere. Det er alle slags belastninger festet til strømnettet, inkludert induktive, resistive og tidvis kapasitive belastninger. Så impedansen er ukjent og foranderlig. Motstanden er veldig liten, noe som betyr at hvis du kobler til en høy strømbelastning, vil spenningen ikke falle mye i det hele tatt.

Trinn 2: Slik skyver du kraften inn i rutenettet

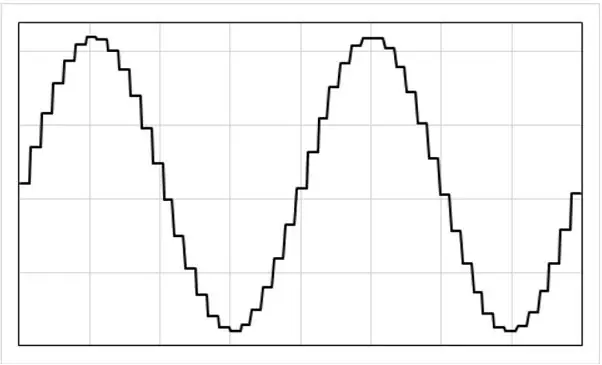
For å skyve strøm inn i nettet må vi syntetisere et signal som nøyaktig samsvarer med frekvensen og fasen til strømnettet, men med en noe høyere spenning.

På grunn av nettets lave motstand er det vanskelig å vite nøyaktig hvor mye høyere å gjøre denne spenningen. Og ettersom RMS -spenningen svinger, må vi sikre at vi svinger med den. Bare det å produsere et fast 50Hz spenningssignal litt høyere enn nettspenningen kommer ikke til å fungere!

PI Kontroll av utgangsstrømmen

Det vi trenger er en kontrollsløyfe der vi måler øyeblikkelig strøm vi skyver inn i nettet og justerer utgangsspenningen automatisk for å drive strømmen vi ønsker. Dette vil effektivt transformere vår utgang til en strømkilde (i stedet for en spenningskilde) som er mer egnet for å drive lave impedanser. Vi kan oppnå dette ved å bruke en PI (Proportional Integral) kontrollløkke:

PI -kontrollløkker er fantastiske! Det er 3 deler til dem:

• Den målte verdien - strømmen vi legger i strømnettet
• Settpunktet - Strømmen vi ønsker å skyve inn i strømnettet
• Utgangen - Signalspenningen som skal genereres

Hver gang vi kaller PID -algoritmen, passerer vi den siste nåværende målingen og settpunktet vi ønsker. Det vil returnere et vilkårlig tall (proporsjonalt med utgangsspenningen som skal genereres).

Vår PID -kontrollalgoritme lar oss velge utgangsstrømmen vi ønsker til enhver tid. For å produsere en 50Hz sinusformet utgangsstrøm må vi kontinuerlig endre den forespurte strømmen på en sinusformet måte.

PID -algoritmen kalles hver 100us (tilsvarer 200 ganger per 50Hz syklus). Hver gang det kalles, er det i stand til å gjøre direkte justeringer av utgangsspenningen og dermed indirekte justere utgangsstrømmen. Som et resultat produserer vi en trinnvis strømutgang som ligner den som vises på bildet, og hvert trinn forekommer hvert 100us. Det gir nok oppløsning.

Feedforward -kontroll

Vi kan massivt redusere arbeidsmengden til PI -kontrolleren ved å også legge til en feedforward -kontroller. Dette er enkelt! Vi vet den omtrentlige utgangsspenningen vi trenger å generere (samme som den øyeblikkelige nettspenningen). PI -kontrolleren kan deretter overlates til den lille ekstra spenningen som trengs for å drive en utgangsstrøm.

I seg selv matcher fremoverkontrolleren vekselretterens utgangsspenning til nettets spenning. Ingen strøm skal strømme hvis vi matcher godt nok. Feedforward -kontrollen gjør derfor 99% av utgangskontrollen.

På grunn av nettets lave motstand vil enhver forskjell i vår FF -utgangsspenning og nettspenningen resultere i en stor strøm. Jeg la derfor til en 1ohm buffermotstand mellom omformeren og nettet. Dette fører til tap, men de er ganske små i den store ordningen.

Trinn 3: Produsere utgangsspenningen ved hjelp av PWM

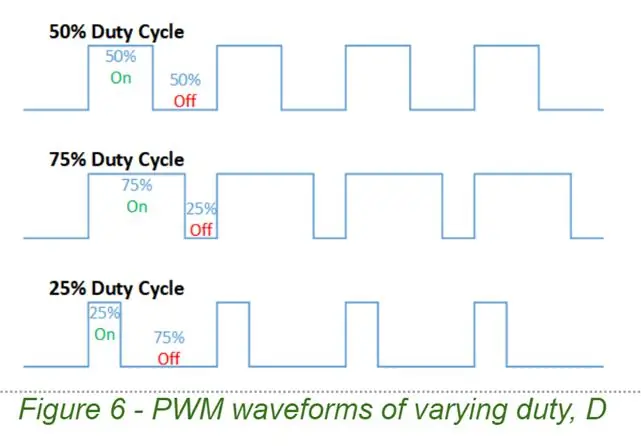
Selv om vi indirekte styrer utgangsstrømmen, er det en utgangsspenning som vi genererer til enhver tid. Vi bruker PWM (Pulse Width Modulation) for å produsere utgangsspenningen vår. PWM-signaler kan enkelt produseres av mikrokontrollere, og de kan forsterkes ved hjelp av en H-bro. De er enkle bølgeformer preget av 2 parametere, frekvensen F og driftssyklus D.

En PWM -bølgeform bytter mellom 2 spenninger, i vårt tilfelle 0v og Vsupply

• Med D = 1.0 er PWM -kurven ganske enkelt likestrøm ved Vsupply
• Med D = 0,5 får vi en firkantbølge med en gjennomsnittlig spenning på 0,5 x Vsforsyning, (dvs. D x Vsupply)
• Med D = 0,1 får vi en pulsert bølgeform med et periodens gjennomsnitt på 0,1 x Vforsyning
• Med D = 0,0 er utgangen en flatlinje (DC ved 0v)

Gjennomsnittsspenningen er nøkkelen. Med et lavpassfilter kan vi fjerne alt annet enn DC-gjennomsnittskomponenten. Så ved å variere PWM -driftssyklusen D, er vi i stand til å gjøre hvilken som helst likspenning ønsket. Søt!

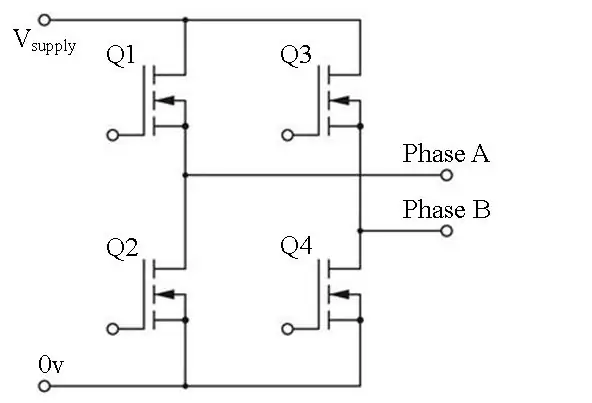
Ansette en H-bro

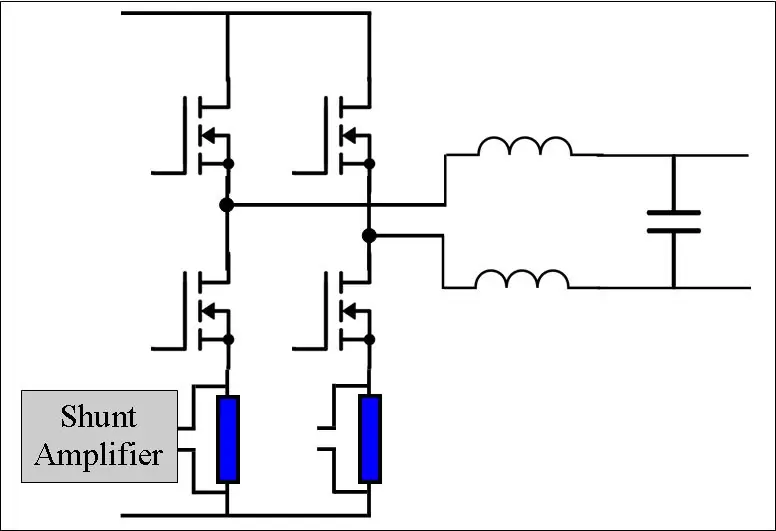
En H-bro består av 4 koblingselementer. Disse kan være BJT, MOSFET eller IGBT. For å produsere den første halvdelen (0 - 180 grader) av sinusbølgen, setter vi fase B lav ved å slå Q3 av og Q4 på (dvs. bruke PWM med D = 0). Vi utfører deretter vår PWMing på fase A. I andre halvdel, hvor VAB er negativt, setter vi fase A lav og bruker vår PWM til fase B. Dette er kjent som bipolar bytte.

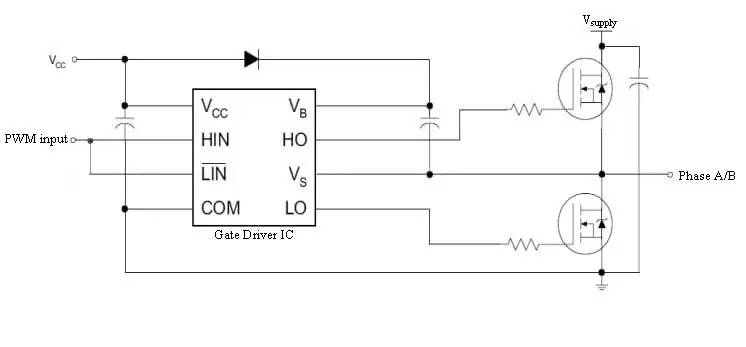
MOSFETene i H-broen må kjøres av en portdriver. Dette er et eget tema, men en enkel brikke kan ta seg av det. DRV8301 dev-brettet inneholder praktisk plassert H-broen, portdrivere og nåværende shunts for oss, noe som gjør dette prosjektet mye lettere.

Trinn 4: Måling av strøm

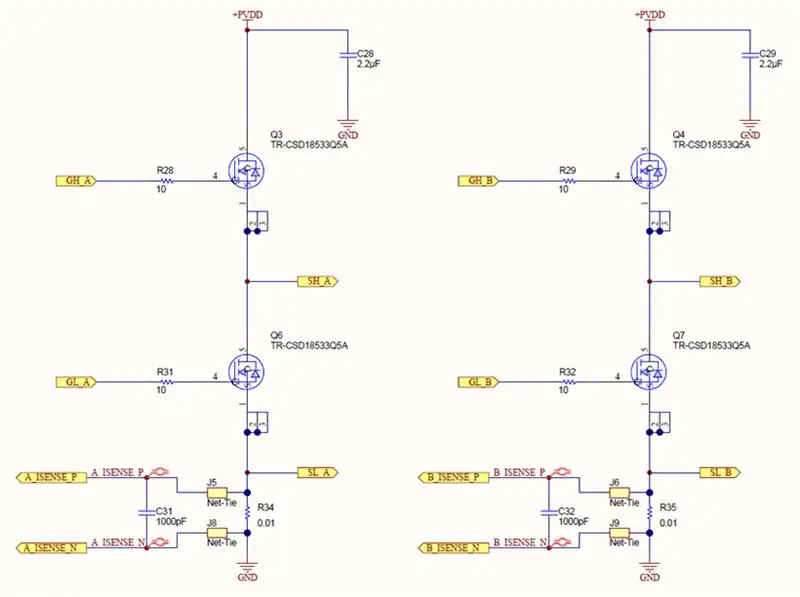
Hvert ben på H-broen har en shuntmotstand og en differensialforsterker. Shuntene våre er 0,01 ohm og forsterkerne er satt til en forsterkning på 40. Derfor utvikler 1 Amp 10mV over shunten som deretter forsterkes til 400mV.

Utgangene fra shuntforsterkerne leses av 12 -biters ADC -er på STM32F407 som kjører i kontinuerlig konverteringsmodus. ADC -ene er satt til å prøve hver shunt ved 110KSPS, og DMA -kontrolleren skriver automatisk konverteringene til en sirkulær buffer på 11 ord i RAM. Når en gjeldende måling er ønsket, kaller vi en funksjon som returnerer medianverdien til denne 11 ordbufferen.

Siden vi ber om strømmålinger hver PID -iterasjon (ved 10KHz), men fyller våre 11 ord ADC -buffere med en hastighet på 110KHz, bør vi få helt ferske data hver PID -iterasjon. Grunnen til å bruke et medianfilter er fordi PWM -bytte kan føre til pigger i blandingen og medianfiltre utrydde falske ADC -prøver veldig effektivt.

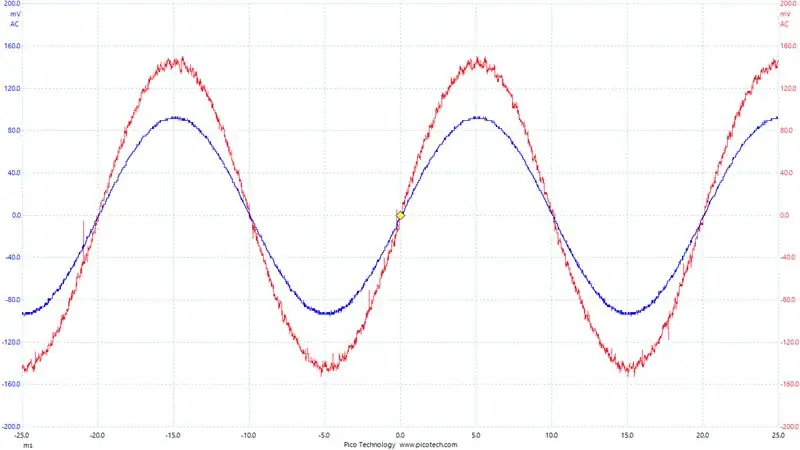
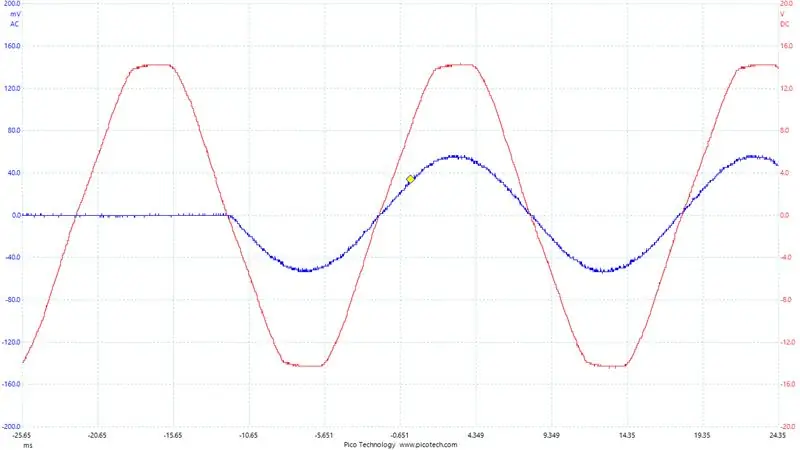
Et viktig poeng å ta her: Hvilken etappe av H-broen bruker vi til nåværende målinger? Vel, det avhenger av hvilket ben vi for tiden PWMing og som bare holdes lavt. Benet som holdes lavt er det vi vil måle strømmen fra siden strømmen alltid flyter gjennom shuntmotstanden på den siden. Til sammenligning, på siden som er PWMed, når høysiden MOSFET er på og lavsiden er av, strømmer det ingen strøm gjennom lavsideshunten. Så vi endrer hvilket ben vi måler strøm på basert på utgangspolariteten til omformeren. Du kan se dette tydelig på bildet, og viser utgangen fra en av shuntforsterkerne over en periode. Tydeligvis ønsker vi å ta avlesninger under den glatte biten.

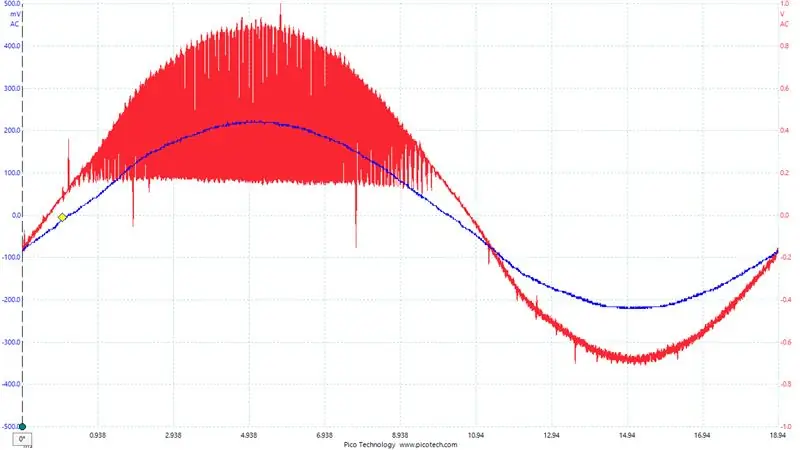
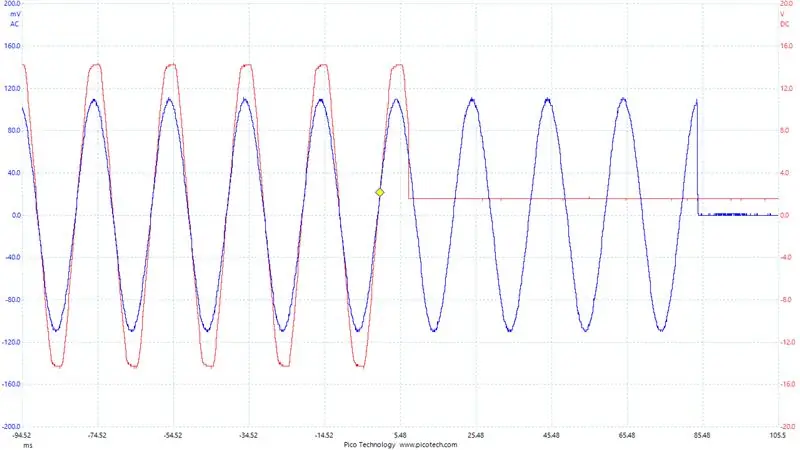
For å hjelpe med å feilsøke våre nåværende avlesninger. Jeg konfigurerte Digital-til-analog-omformeren på STM32F407. Jeg skrev de nåværende avlesningene jeg fikk og målte utgangen. Du kan se dette i det endelige bildet, det blå er spenningen over utgangsbuffermotstanden (dvs. utgangsstrømmen/1,1 ohm) og det røde signalet er vår DAC -utgang.

Trinn 5: Filtrering av utdata

Utgangsfilteret er en sentral del av designet. Vi trenger disse egenskapene fra det:

1. Blokker alle høyfrekvente bytter, men send et 50Hz signal
2. Lavt tap
3. Ikke for å resonere!
4. For å takle de involverte strømmer og spenninger

Fourier -transformasjonen av et PWM -signal med frekvens F, Driftssyklus D, mellom 0 - V forsyningsspenning er: (D x Vsupply) + Sinusbølger ved grunnfrekvensen F, og harmoniske deretter

Dette er strålende! Det betyr at hvis vi sender vårt PWM -signal gjennom et lavpassfilter som blokkerer PWM -fundamentet og alt ovenfor. Vi sitter akkurat igjen med likestrømsspenningen. Ved å variere driftssyklusen kan vi enkelt produsere hvilken som helst spenning vi vil ha mellom 0 - Vforsyning som forklart.

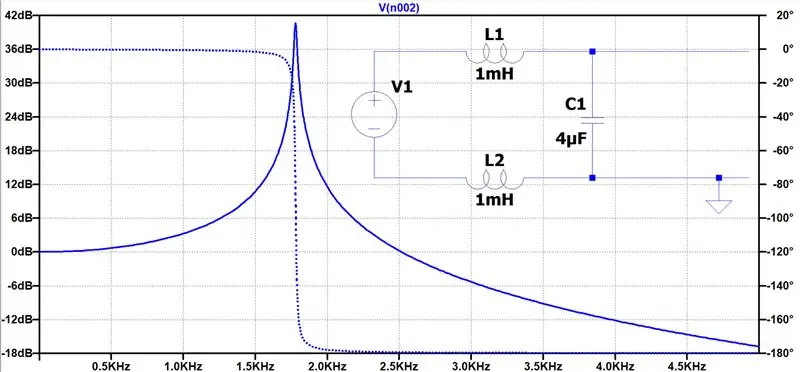
Basert på de ønskede egenskapene nevnt ovenfor kan vi designe utgangsfilteret. Vi trenger et lavpasfilter laget med minimal motstand for å unngå tap. Derfor bruker vi bare induktorer og kondensatorer. Hvis vi velger en resonansfrekvens mellom 1 - 2KHz, vil vi unngå resonans siden vi ikke injiserer noen signaler i nærheten av denne frekvensen. Her er filterdesignet vårt. Vi tar utgangen vår som spenningen over C1.

Ved å velge L1 = L2 = 440uH, C1 = 8.4uF beregner vi en resonansfrekvens på 1.85KHz. Dette er også realistiske komponentverdier.

Det er viktig å sørge for at induktorene våre ikke begynner å mette ved strømmen vi forventer. Induktorene jeg har brukt har en metningsstrøm på 3A. Dette vil være den begrensende faktoren for kretsens utgangseffekt. Kondensatorspenningsvurderingen er også viktig å vurdere. Jeg bruker litt 450v keramikk som er veldig overkill i dette tilfellet!

Bodeplottet (for litt forskjellige L/C -verdier) er generert ved bruk av LTspice. Det viser oss dempningen påført forskjellige inngangsfrekvenser. Vi kan tydelig se resonansfrekvensen på 1,8KHz. Det viser at et 50Hz -signal er nesten helt uforfalsket, mens jeg kan fortelle deg at et 45 KHz -signal dempes med 54dB!

Så la oss velge vår PWM -bærefrekvens til ~ 45KHz. Ved å velge høyere PWM -bærefrekvenser, kan filterfrekvensen gjøres høyere. Det er bra fordi det gjør L- og C -verdiene mindre. Det betyr mindre og billigere komponenter. Ulempen er at høyere PWM -koblingsfrekvenser introduserer større tap i transistorbryterne.

Trinn 6: Synkronisering av fase og frekvens

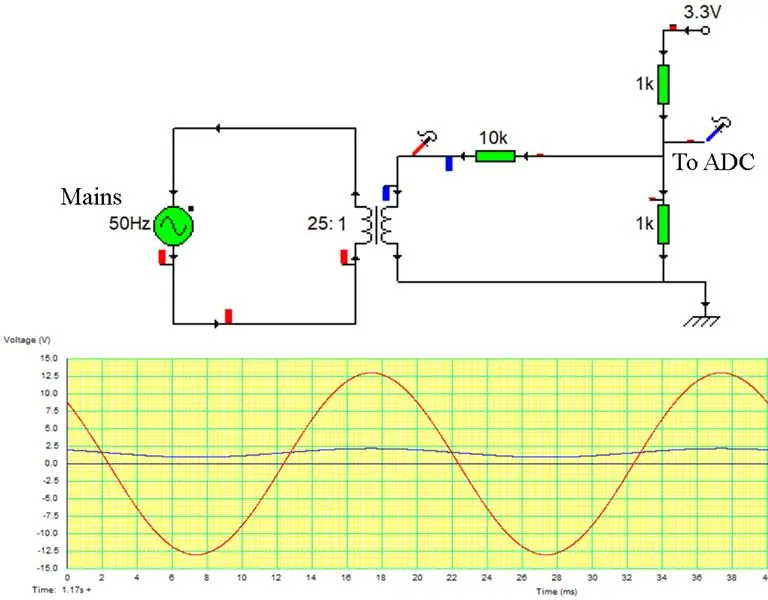
Synkronisering med nettfasen og frekvensen er det som gjør en grid tie inverter. Vi bruker en digital implementering av en PLL (Phase Locked Loop) for å oppnå nøyaktig fasesporing av nettsignalet. Vi gjør dette ved å:

1. Prøvetaking av nettspenningen
2. Produserer et lokalt sinusformet signal på 50 Hz
3. Sammenligning av fasen mellom vårt lokale signal og nettsignalet
4. Justering av frekvensen til det lokale signalet til faseforskjellen mellom de 2 signalene er null

1) Prøvetaking av nettspenningen

Vi konfigurerer en tredje ADC -kanal for å lese linjespenningen. Dette får vi ved spenningsdeling av en transformatorkran som vist. Dette gir en skalert spenning på rundt 1,65v som nøyaktig representerer nettspenningen.

2) Å produsere et lokalt 50Hz sinusformet signal Det er enkelt å produsere vår egen lokale 50Hz sinusbølge. Vi lagrer en oppslagstabell med 256 sinusverdier. Vår simulerte sinusverdi oppnås enkelt ved hjelp av en oppslagsindeks som roterer trinnvis gjennom tabellen.

Vi må øke indeksen vår med nøyaktig riktig hastighet for å få et 50Hz -signal. Nemlig 256 x 50Hz = 12, 800/s. Vi gjør dette ved å bruke timer9 klokket til 168MHz. Ved å vente 168MHz/12800 = 13125 klokker, vil vi stige indeksen til riktig hastighet.

3) Sammenligning av fasen mellom vårt lokale signal og nettsignalet Dette er den kule delen! Hvis du integrerer produktet av cos (vekt) x sin (vekt) over en periode, er resultatet null. Hvis faseforskjellen er noe annet enn 90 grader får du et null -nummer. Matematisk:

Integral [Asin (t) x Bsin (t + φ)] = Ccos (φ)

Dette er flott! Det lar oss sammenligne nettsignalet, sin (ωt) med vårt lokale signal, sin (⍵t + φ) og få en verdi.

Det er imidlertid et problem som må løses: Hvis vi ønsker å ha signalene våre til å forbli i fase, må vi justere vår lokale frekvens for å holde Ccos (φ) termen maksimal. Dette vil ikke fungere veldig bra, og vi får dårlig fasesporing. Dette er fordi d/dφ for ɑcos (φ) er 0 ved φ = 0. Dette betyr at Ccos (φ) -begrepet ikke vil variere veldig med faseendringer. Gir det mening?

Det ville være langt bedre å faseskifte det samplede nettsignalet med 90 grader slik at det blir cos (ωt + φ). Så har vi dette:

Integral [Asin (t) Bcos (t + φ)] = Csin (φ)

Det er enkelt å introdusere et 90 graders faseforskyvning. Vi setter bare inn ADC -spenningsprøvene til strømnettet i den ene enden av en buffer og tar dem ut et antall prøver senere, tilsvarende et faseskift på 90 grader. Siden nettfrekvensen neppe varierer fra 50Hz, fungerer en enkel tidsforsinkelsesteknikk strålende.

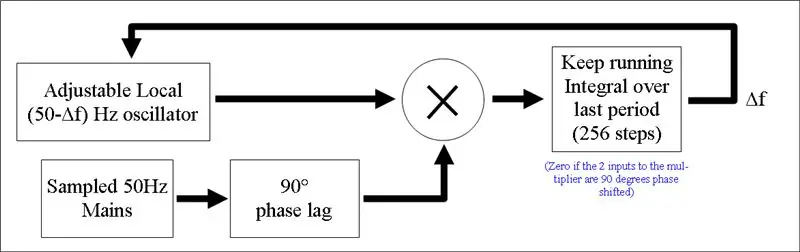
Vi multipliserer nå vårt 90 graders faseforskyvede nettsignal med vårt lokale signal og beholder en løpende integral av produktet den siste perioden (dvs. over de siste 256 verdiene).

Resultatet vi vet vil være null hvis de 2 signalene nøyaktig holdes 90 grader fra hverandre. Dette er fantastisk fordi det opphever faseskiftet vi nettopp brukte på nettsignalet. Bare for å klargjøre, i stedet for å maksimere det integrerte begrepet, prøver vi å holde det null, og vi faseforskyver vårt nettsignal. 90 graders faseskift som ble introdusert av disse 2 endringene, avbryter hverandre.

Så hvis Integral_Result <0 vet vi at vi må øke vår lokale oscillatorfrekvens for å bringe den tilbake i fase med strømnettet, og omvendt.

4) Justere frekvensen til det lokale signalet Denne biten er enkel. Vi justerer ganske enkelt perioden mellom å øke gjennom indeksen vår. Vi begrenser hvor raskt vi kan korrigere faseforskjellen, i hovedsak ved å filtrere ut falske whatevers. Vi gjør dette ved hjelp av en PI -kontroller med et veldig lite I -begrep.

Og det er det. Vi har låst vår lokale sinusbølge -oscillator (som setter utgangsstrømens settpunkt) for å være i fase med nettspenningen. Vi har implementert en PLL -algoritme, og den fungerer som en drøm!

Å øke frekvensen til vår lokale oscillator reduserer også faseforskyvningen på nettsignalet. Siden vi begrenser frekvensjusteringen til +/- 131 flått (+/- ~ 1%), påvirker vi faseforskyvningen maksimalt med +/- 1 °. Dette kommer ikke til å ha betydning i det hele tatt mens fasene synkroniseres.

Teoretisk sett hvis strømfrekvensen avviket med mer enn 0,5 Hz, ville vi miste faselåsen. Dette er på grunn av den ovennevnte begrensningen for hvor mye vi kan justere vår lokale oscillatorfrekvens. Det kommer imidlertid ikke til å skje med mindre nettet er i ferd med å mislykkes. Vår anti-øybeskyttelse vil uansett sparke inn på dette tidspunktet.

Vi utfører en nullkryssingsdeteksjon ved oppstart for å prøve vårt beste for å starte signalene inphase fra forskyvningen.

Trinn 7: Anti-islanding

Wikipedia har en kjempeflott artikkel om teknikker for øyfart og øyfare. Det innebærer også at folk hveser og klapper mer enn nødvendig når det gjelder dette emnet. "Å, du kan ikke bygge din egen grid tie inverter, du vil drepe noen osv. Etc."

Som forklart bedre av wikipedia -artikkelen bruker vi et par sikkerhetstiltak som sammen gir tilstrekkelig beskyttelse (etter min mening):

1. Under-/overspenning
2. Under/Over frekvens

Vi kan oppdage disse situasjonene ved å analysere vår samplede skalerte nettspenning. Hvis noe går galt, deaktiver H-broen og vent på at ting skal gå tilbake til det normale.