3D -rekonstruksjon fra et enkelt foto: 8 trinn

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-30 11:20

Oppgaven med 3D -rekonstruksjon er vanligvis forbundet med kikkert. Alternativt kan du flytte et enkelt kamera rundt objektet. I mellomtiden, hvis formen på objektet er kjent, kan oppgaven løses fra et enkelt foto. Det vil si at du bare har ett kamera og at det ikke beveger seg. La oss se hvordan du gjør det trinnvis. Vi vil bruke Rubiks kube fordi den er godt standardisert og har et rikt sett med funksjoner. Det kan betraktes som et veldig enkelt objekt og samtidig en komplisert konstruksjon. Så maskinsynet må overgå betydelige hindringer for å fullføre oppgaven.

Trinn 1: Vurder oppgavens kompleksitet

Ved første øyekast er oppgaven enkel. Finn den sentrale knuten der 3 kanter av kuben kommer sammen og tegne disse kantene. Fra koordinatene er det mulig å beregne avstanden fra kameraet og rotasjonsvinklene. Problemet er at disse linjene ikke eksisterer. Fra det venstre bildet ser du at hver kant er representert med 2 parallelle linjer. Videre viser bildet øverst til høyre at hver av dem er delt inn i 3 segmenter. Videre, hvis vi bruker en variant av den populære Hough -transformasjonen som kan oppdage linjesegmenter, utfører den oppgaven med noen feil som gjør detektering av den sentrale knuten umulig. Hvis endene ikke når hverandre, er det ikke et enkelt punkt. Hvis deteksjonen overskrider enden, vil det se ut som knuten i midten av kanten som du ser på de 2 gjenværende bildene.

Trinn 2: Finn den riktige tilnærmingen

Når for mange detaljer gjør deterministiske algoritmer ubrukelige, er det på tide å vurdere sannsynlighetsmetoden. Hvis vi beregner gjennomsnittlige parametere for bildet, vil feilene deres bli vesentlig redusert, og paradoksalt nok vil metoden bli mer pålitelig. Standard Hough -transformasjon sender ikke ut linjesegmenter. Bare dens helling theta og avstanden rho fra koordinatopprinnelsen. De danner Hough -romdelen som er vist ovenfor. Her tilsvarer theta den horisontale aksen. Lyse flekker markerer mulige linjer på bildet. Vær oppmerksom på at flere slike flekker ligger over hverandre. Ikke rart, på bildet vårt er det mange parallelle linjer. De har samme theta og forskjellige rho.

Trinn 3: Beregn Theta Histogram

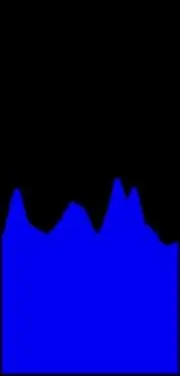
La oss oppdage slike klynger. For dette formålet vil vi oppsummere avlesninger for alle prikkene i Hough -rommet med samme theta. Du ser det tilsvarende histogrammet på illustrasjonen. Noen notater om målinger. Når du arbeider med bilder i pikselkoordinater, går X -aksen som vanlig, men Y peker nedover slik at koordinatens opprinnelse er i øvre venstre hjørne, og theta skal måles fra X -aksen med klokken. Når du husker at hele sveipingen av theta på bildet er 180 grader, kan du omtrent kontrollere at 3 store topper representerer 3 dominerende bakker på bildet.

Trinn 4: Beregn Rho Histogram

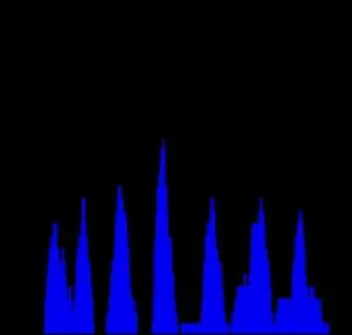
Nå som vi kjenner 3 hovedklynger av parallelle linjer, la oss skille linjer innenfor hver av dem. Vi kan gjenta den samme tilnærmingen. La oss ta en kolonne fra Hough -plassen som tilsvarer en topp på theta -histogrammet. Deretter vil vi beregne et annet histogram der X -aksen representerer rho -verdi og Y - oppsummerte avlesninger for denne rho. Selvfølgelig vil summen være mindre, så dette diagrammet er ikke så jevnt. Likevel er topper godt synlige og antallet av dem (7) tilsvarer nøyaktig antall parallelle linjer på kildebildet. Dessverre er ikke alle diagrammene så perfekte, men prinsippet er klart.

Trinn 5: Finn den sentrale knuten

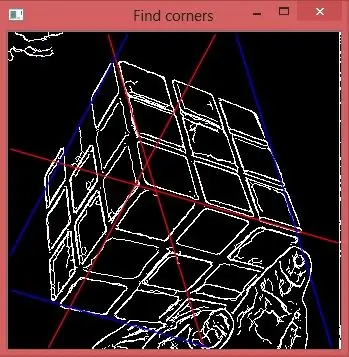
Hvis vi tar den sentrale toppen på rho histogram for hver theta, får vi 3 linjer som er røde på bildet. Krysset deres markerer det nødvendige punktet.

Trinn 6: Velg mellom 2 alternativer

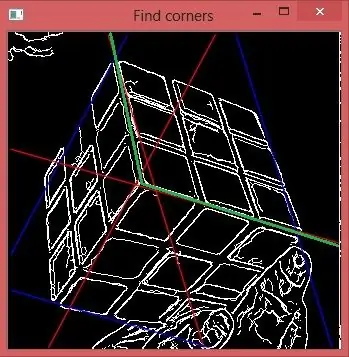
Du ser at hver linje går fra det sentrale punktet i begge retninger. Hvordan bestemme riktig halvdel? La oss ta theta3. Anta at vi tar den nedre delen av denne linjen. La oss beregne enda en Hough -plass bare for delen av bildet fra 2 grønne linjer til øvre høyre hjørne av bildet. Lag deretter theta histogram for det. Du ser at den tredje toppen forsvant helt, så vi har gjort det riktige valget.

Trinn 7: Bestem de eksterne hjørnene

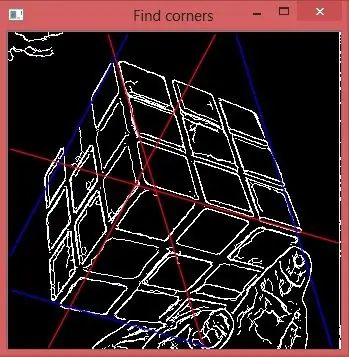
Nå kan vi bruke den første og den siste toppen på rho -histogrammer for å tegne blå linjer som kutter de røde kantene og markerer resten av hjørnene. Oppgaven er løst.

Trinn 8: Prøv det i praksis

Illustrasjonene for denne instruksjonsboken ble laget med Perception 1.0. Dette er gratis programvare som bruker OpenCV - et kraftig bibliotek for datasyn. Det kan også være knyttet til WinNB som ble brukt i min andre Instructable og dermed gi visjonsevne for robotikk. Du kan laste ned begge programmene fra nbsite. For installasjon, bare kjør den nedlastede exe -filen. Senere kan du fjerne det ved hjelp av standardverktøyet i Windows. Nettstedet inneholder også ressurser om datasyn og relaterte emner. I Perception finner du den beskrevne metoden for 3D -rekonstruksjon så vel som mange andre. Fordelen med dette programmet er at det sender ut det endelige resultatet sammen med mellomliggende data. Du kan undersøke hvordan datasyn fungerer uten å være programmerer. Når det gjelder input, har hver metode spesielt valgt typiske prøver. Selvfølgelig kan du bruke din egen også. Det er mulig å legge inn bilder fra en fil eller fra datamaskinens kamera. Kontakt meg gjerne med spørsmål eller forslag.