Brettspill Kunstig intelligens: Minimax -algoritmen: 8 trinn

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-30 11:22

Har du noen gang lurt på hvordan datamaskinene du spiller mot i sjakk eller brikker er laget? Vel, se ikke lenger enn denne Instructable, for den vil vise deg hvordan du lager en enkel, men effektiv kunstig intelligens (AI) ved hjelp av Minimax -algoritmen! Ved å bruke Minimax -algoritmen gjør AI godt planlagte og gjennomtenkte trekk (eller etterligner i det minste en tankeprosess). Nå kan jeg bare gi deg koden for AI som jeg laget, men det ville ikke være morsomt. Jeg skal forklare logikken bak datamaskinens valg.

I denne instruksen vil jeg lede deg gjennom trinnene for hvordan du lager en AI for Othello (AKA Reversi) i python. Du bør ha en mellomliggende forståelse av hvordan du koder i python før du takler dette prosjektet. Her er noen få gode nettsteder å se på for å forberede deg på denne instruksjonsfulle: w3schools eller learnpython. På slutten av denne instruksjonsboken bør du ha en AI som vil gjøre beregnede trekk og skal kunne beseire de fleste mennesker.

Siden denne Instructable først og fremst vil håndtere hvordan du lager en AI, vil jeg ikke forklare hvordan du designer et spill i python. I stedet vil jeg gi koden for spillet hvor et menneske kan spille mot et annet menneske og endre det slik at du kan spille et spill der et menneske spiller mot AI.

Jeg lærte å lage denne AI gjennom et sommerprogram på Columbia SHAPE. Jeg hadde det bra der, så ta en titt på nettstedet deres for å se om du er interessert.

Nå som vi fikk logistikken ut av veien, la oss begynne å kode!

(Jeg la et par notater i bildene, så sørg for å se på dem)

Rekvisita

Dette er enkelt:

1) Datamaskin med et pytonmiljø som Spyder eller IDLE

2) Last ned filene for Othello -spillet fra min GitHub

3) Hjernen din med tålmodighet installert

Trinn 1: Last ned de nødvendige filene

Når du går inn på min GitHub, bør du se 5 filer. Last ned alle 5 og legg dem alle i samme mappe. Før vi kjører spillet, åpner du alle filene i spyder -miljøet.

Her er hva filene gjør:

1) othello_gui.py denne filen lager spillbrettet for spillerne å spille på (enten det er menneske eller datamaskin)

2) othello_game.py denne filen spiller to datamaskiner mot hverandre uten tavlen og viser bare poengsummen og flytt posisjoner

3) ai_template.py det er her du vil sette all koden din for å lage din AI

4) randy_ai.py dette er en ferdiglaget AI som velger trekk tilfeldig

5) othello_shared.py en haug med forhåndsdefinerte funksjoner som du kan bruke til å lage din AI, for eksempel å se etter tilgjengelige trekk, poengsummen eller brettstatus

6) De tre andre filene: Puma.py, erika_5.py og nathan.py, laget av henholdsvis meg, Erika og Nathan fra SHAPE -programmet, dette er tre forskjellige AI -er med unike koder

Trinn 2: Hvordan åpne og spille Python Othello

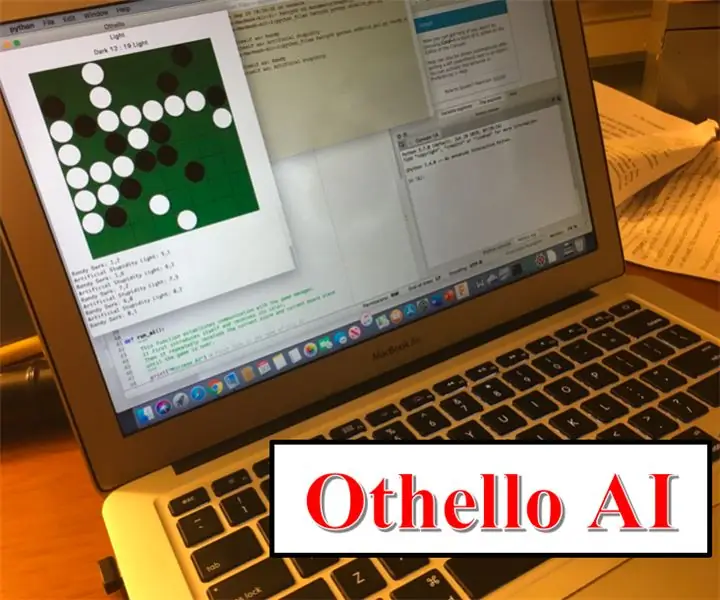
Når du har alle filene åpne, skriver du "run othello_gui.py" nederst til høyre på skjermen og trykker enter i IPython-konsollen. Eller i Mac -terminalen skriver du "python othello_gui.py" (etter at du er i riktig mappe selvfølgelig). Deretter skal det dukke opp et brett på skjermen. Denne modusen er menneskelig vs menneskelig modus. Lys går andre og mørkt først. Se på videoen min hvis du er forvirret. i På toppen er det poengsummen til hver fargeflise. For å spille, klikk på en gyldig flytteplass for å plassere en flis der, og gi deretter datamaskinen til motstanderen din som vil gjøre det samme og gjenta.

Hvis du ikke vet hvordan du spiller Othello, kan du lese disse reglene fra nettstedet ultra boards:

Svart beveger seg alltid først. Et trekk gjøres ved å plassere en plate med spillerens farge på brettet i en posisjon som "flankerer" en eller flere av motstanderens plater. En plate eller rad med plater flankeres når den er omgitt i endene av plater med motsatt farge. En plate kan flankere et hvilket som helst antall plater i en eller flere rader i hvilken som helst retning (horisontalt, vertikalt, diagonalt)…. (les ferdig på nettstedet deres)

Forskjellen mellom det opprinnelige spillet og dette pythonspillet er at når det ikke er noen gyldige trekk igjen for en spiller, slutter spillet

Nå som du kan spille spillet med en venn, la oss lage en AI som du kan spille med.

Trinn 3: Minimax -algoritme: Generering av scenarier

Før vi snakker om hvordan du skriver dette i kode, la oss gå over logikken bak det. Minimax-algoritmen er en beslutningstaker, back-tracking-algoritme og brukes vanligvis i to-spiller, turbaserte spill. Målet med denne AI er å finne det neste beste trekket og de følgende beste trekkene til det vinner spillet.

Nå, hvordan ville algoritmen avgjøre hvilket trekk som er det beste trekket? Stopp og tenk på hvordan du ville velge det neste trekket. De fleste ville valgt det trekket som ville gi dem flest poeng, ikke sant? Eller hvis de tenkte fremover, ville de velge trekket som ville skape en situasjon der de kunne få enda flere poeng. Den siste tankegangen er måten Minimax -algoritmen tenker på. Det ser fremover til alle fremtidige brettoppsett og gjør det trekket som vil føre til flest poeng.

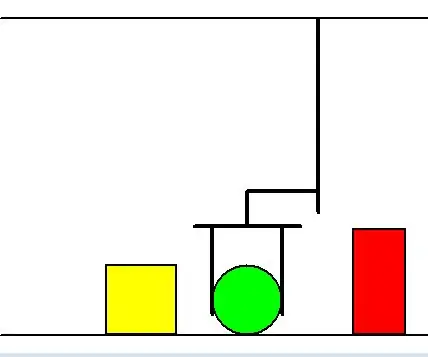
Jeg kalte dette en backtracking -algoritme, fordi den starter med først å opprette og evaluere alle fremtidige brettstater med tilhørende verdier. Dette betyr at algoritmen vil spille spillet så mange som det trenger (gjøre bevegelsene for seg selv og motstanderen) til hvert scenario i spillet har spilt. For å holde oversikt over alle brettstatene (scenarier) kan vi tegne et tre (se på bildene). Treet på bildet ovenfor er et enkelt eksempel på et spill med Connect 4. Hver brettkonfigurasjon kalles en brettstat og stedet på treet kalles en node. Alle nodene nederst på treet er de endelige brettstatene etter å ha gjort alle trekkene. Noen brettstater er åpenbart bedre for den ene spilleren enn den andre. Så nå må vi få AI til å velge hvilken styrestat den vil komme til.

Trinn 4: Minimax: Evaluering av bordkonfigurasjoner

For å gi verdiene til brettstatene, må vi lære strategiene for spillet vi spiller: i dette tilfellet strategiene til Othello. Fordi dette spillet er en kamp om å snu motstanderens og platene dine, er de beste plateposisjonene de som er stabile og ikke kan vendes. Hjørnet, for eksempel, er stedet hvor det ikke kan endres til en annen farge når en plate plasseres. Dermed ville dette stedet være ekstremt verdifullt. Andre gode posisjoner inkluderer sidene av brettet som gjør at du kan ta mange steiner. Det er flere strategier på dette nettstedet.

Nå kan vi tilordne verdier til stillingene for hvert styrestatsstyre. Når en posisjon er opptatt av AI -brikken, gir du et visst antall poeng avhengig av posisjonen. For eksempel på en brettstat hvor AI -brikken er i hjørnet, kan du gi en bonus på 50 poeng, men hvis den var på et ugunstig sted, kan brikken ha en verdi på 0. Etter å ha tatt hensyn til alle verdiene til stillingene, gir du styret en verdi. For eksempel, hvis AI har en brikke i hjørnet, kan brettstaten ha en score på 50, mens en annen brettstat med AI -brikken i midten har en score på 10.

Det er mange måter å gjøre dette på, og jeg har tre forskjellige heuristikker for å evaluere brettstykkene. Jeg oppfordrer deg til å lage din egen type heuristikk. Jeg lastet opp tre forskjellige AI -er til min github av tre forskjellige produsenter, med tre forskjellige heuristikker: Puma.py, erika5.py, nathanh.py.

Trinn 5: Minimax -algoritme: Velge beste trekk

Nå ville det være fint hvis AI bare kunne velge alle trekkene for å komme til brettstaten med høyest poengsum. Men husk at AI også valgte trekkene for motstanderen da den genererte alle brettstatene, og hvis motstanderen er smart, vil den ikke tillate AI å nå den høyeste brettpoengsummen. I stedet ville en smart motstander gjøre grepet for å få AI til å gå til den laveste brettstaten. I algoritmen kaller vi de to spillerne en maksimerende spiller og en minimerende spiller. AI ville være den maksimale spilleren siden den ønsker å få flest poeng for seg selv. Motstanderen vil være den minimerende spilleren siden motstanderen prøver å gjøre trekket der AI får færrest poeng.

Når alle bretttilstandene er generert og verdiene er tilordnet brettene, begynner algoritmen å sammenligne brettstatene. På bildene opprettet jeg et tre for å representere hvordan algoritmen ville velge bevegelsene. Hver splittelse i grenene er et annet trekk AI eller motstanderen kan spille. Til venstre for radene med noder skrev jeg om den maksimerende eller minimerende spilleren går. Den nederste raden er alle brettstatene med sine verdier. Inne i hver av disse nodene er et tall, og det er poengsummene vi tildeler hvert av brettene: jo høyere de er, jo bedre er det for AI å ha.

Definisjoner: overordnet node - en node som resulterer eller oppretter noder under den; opprinnelsen til barneknuter - nodene som kommer fra den samme overordnede noden

De tomme nodene representerer hvilken bevegelse AI vil gjøre for å komme til den beste brettstaten. Det starter med å sammenligne barna til noden lengst til venstre: 10, -3, 5. Siden den maksimerende spilleren ville gjøre trekket, ville den velge det trekket som ville gi det flest poeng: 10. Så vi velger og lagrer det bevege deg med tavle score og skrive det i den overordnede noden. Nå som 10 er i den overordnede noden, er det nå de minimerende spillerne. Noden som vi vil sammenligne 10 med er imidlertid tom, så vi må vurdere den noden først før minimeringsspilleren kan velge. Så vi går tilbake til den maksimerende spillerens tur og sammenligner barna til den tilstøtende noden: 8, -2. Maksimering vil velge 8, og vi skriver det i den tomme overordnede noden. Nå som algoritmen er ferdig med å fylle ut de tomme plassene for barna til en node over den, kan den minimerende spilleren sammenligne disse barna - 10 og 8 og velge 8. Algoritmen gjentar deretter denne prosessen til hele treet er fylt ut. På slutten av dette eksemplet har vi poengsummen 8. Det er den høyeste brettstaten AI kan spille for å anta at motstanderen spiller optimalt. Så AI vil velge det første trekket som fører til 8 -brettstatusen, og hvis motstanderen spiller optimalt, bør AI spille alle trekkene for å komme til brettstatus 8. (Følg notatene på bildene mine)

Jeg vet det var mye. Hvis du er en av de typene som trenger å få noen til å snakke med deg for å forstå noe, her er et par videoer jeg så på for å hjelpe meg med å forstå ideen bak dette: 1, 2, 3.

Trinn 6: Minimax -algoritme: Pseudokode

Etter at du forstår logikken bak minimax -algoritmen, kan du se på denne pseudokoden (funksjonene som er universelle for alle koder) fra wikipedia:

funksjon minimax (node, depth, maximizingPlayer) er

hvis dybde = 0 eller node er en terminal node da

returnere den heuristiske verdien av node

hvis maximizingPlayer da

verdi: = −∞

for hvert nodebarn

verdi: = maks (verdi, minimaks (barn, dybde - 1, FALSK))

returverdi

annet (* minimering av spilleren *)

verdi: = +∞

for hvert nodebarn

verdi: = min (verdi, minimaks (barn, dybde - 1, SANN))

returverdi

Dette er en rekursiv funksjon, noe som betyr at den kaller seg selv om og om igjen til den når et stopppunkt. Først tar funksjonen inn tre verdier, noden, dybden, og hvis tur det er. Nodeverdien er stedet der du vil at programmet skal begynne å søke. Dybden er hvor langt du vil at programmet skal søke. For eksempel, i mitt treeksempel har den en dybde på 3, fordi den søkte i alle brettstatene etter 3 trekk. Selvfølgelig vil vi at AI skal kontrollere hver brettstat og velge en vinnende seier, men i de fleste spill der det er tusenvis om ikke millioner av brettkonfigurasjoner, vil ikke den bærbare datamaskinen hjemme kunne behandle alle disse konfigurasjonene. Så vi begrenser AIs søkedybde og får den til å gå til den beste tavelstaten.

Denne pseudokoden gjengir prosessen jeg forklarte i de to foregående trinnene. La oss nå ta dette et skritt videre og rette dette i python -koden.

Trinn 7: Lag din AI med Ai_template.py

Før du ser på min Minimax AI-kode, må du prøve å lage din egen AI med filen ai_template.py og pseudokoden vi snakket om i det siste trinnet. Det er to funksjoner i ai -malen kalt: def minimax_min_node (brett, farge) og def minimax_max_node (brett, farge). I stedet for å ha minimax -funksjonen kaller seg rekursivt, har vi to forskjellige funksjoner, som kaller hverandre. For å lage det heuristiske for å evaluere styretilstander, må du lage din egen funksjon. Det er forhåndsdefinerte funksjoner i othello_shared.py -filen som du kan bruke til å bygge din AI.

Når du har din AI, kan du prøve å kjøre den mot, randy_ai.py. For å kjøre to ais mot hverandre, skriver du inn "python othello_gui.py (sett inn ai -filnavn).py (sett inn filnavn).py" i mac -terminalen eller skriv "run othello_gui.py (sett inn ai -filnavn).py (sett inn filnavn).py "og kontroller at du er i riktig katalog. Se også på videoen min for de nøyaktige trinnene.

Trinn 8: På tide å få AI til å kjempe

Skaff deg en haug med datavennene dine og få dem til å designe sin egen AI! Deretter kan du lage en konkurranse og få AI -hertugen din til å gå ut. Forhåpentligvis, selv om du ikke kunne bygge din egen AI, var du i stand til å forstå hvordan minimax -algoritmen fungerer. Hvis du har spørsmål, kan du legge inn spørsmål i kommentarene nedenfor.