Eyeballing Eyeball's resept: et BME60B -prosjekt: 9 trinn

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-30 11:21

Av: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

Forstørrelse er en av de viktigste egenskapene som er tilstede for lesebriller, som er klassifisert etter deres resept for dioptrier. I følge Michigan Technology University er en diopter en brennvidde på linsen, vanligvis målt i mm, i meter (Michigan Technology University). Fordi lesebriller har konvekse linser, vil brennvidden være positiv, noe som får dioptrene til å være positive også (HyperPhysics). Brennvidden øker etter hvert som avstanden mellom objektet kommer lenger vekk fra det faktiske objektivet, og dette fører til at diopterne reduseres siden de er omvendt proporsjonale. Derfor vil det å ha lesebriller med flere dioptrier hjelpe linsen med å zoome inn i visningen, slik at det kan virke som om brennvidden er mindre ved å øke verdien av dioptrene.

Koden som presenteres vil bli brukt til å forutsi dioptrien til et objektiv med ukjent resept. To innganger brukes til å beregne reseptet: et fotografi av den kontrollerte bakgrunnen uten bruk av linser, og et annet fotografi med samme bakgrunn, men gjennom det valgte objektivet. Programmet vil måle forvrengningen mellom disse to fotografiene. Derfra vil vi kunne estimere linsens dioptri og produsere et resultat som brukeren kan se.

For denne instruksjonsmåten trenger du:

• Et svart-hvitt sjakkbrettmønster trykt på et 11x8,5 i papirark
• Et kamera med muligheten til å låse fokus
• Et stativ, eller noe lignende for å sikre kameraet
• Ulike resepter på lesebriller
• MATLAB

Trinn 1: Ta bilder

For å beregne forstørrelsen på et objektiv, må du kunne sammenligne det med objektets faktiske størrelse. For dette prosjektet vil vi sammenligne et forstørret bilde med et kontrollbilde.

Dermed er det første trinnet å ta to bilder av det samme bildet - det første gjennom bare kameraet, og det andre gjennom linsen på lesebrillene du vil teste.

Du tar et bilde av et 8,5 x 11 tommer svart og hvitt brett med et 1 -tommers rutenett. Sett opp kameraet 11in vekk fra sjakkbrettet. Lås fokuset på sjakkbrettet før du tar bildene.

Ta et bilde av brettet uten lesebrillene. Deretter, uten å bevege deg på noe, plasserer du lesebrillene foran kameraet og tar det andre bildet.

Sørg for at kameraets posisjon ikke beveger seg mellom bildene. Det eneste som bør endre seg mellom de to bildene er tilstedeværelsen av brilleglasset foran kameraet.

Når du er ferdig med bildene, laster du dem opp til datamaskinen.

Trinn 2: Last inn bildene i MATLAB

Åpne et nytt skript.

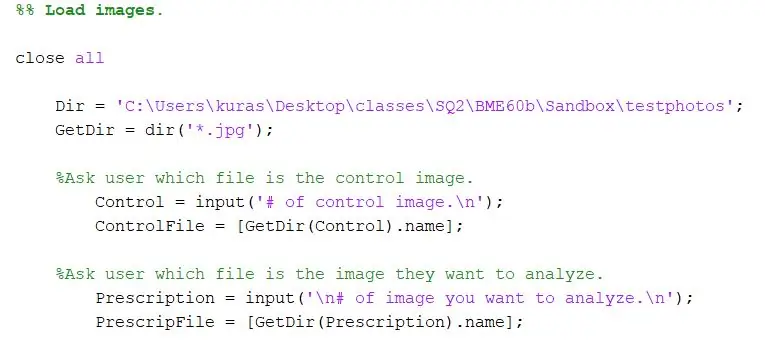
Angi først katalogen der bildene er lagret. Bruk deretter dir -funksjonen til å trekke ut-j.webp

Dir = 'C: / Users / kuras / Desktop / classes / SQ2 / BME60b / Sandbox / testphotos'; GetDir = dir ('*. Jpg');

For prosjektet vårt ønsket vi å be brukeren av programmet om hvilke filer de ønsket å sammenligne. Den første delen ber brukeren om å spesifisere kontrollbildet, og den andre ber brukeren om å spesifisere testbildet.

• %Spør brukeren hvilken fil som er kontrollbildet.
• Kontroll = input ('# av kontrollbilde. / N');
• ControlFile = [GetDir (Control).name]
• %Spør brukeren hvilken fil som er bildet de vil analysere.
• ChooseFile = input ('\ n# av bildet du vil analysere. / N');
• PrescripFile = [GetDir (ChooseFile).name];

Trinn 3: Bildeanalyse

Et farget bilde i MATLAB er av størrelsen MxNx3, mens et gråtonebilde er MxN. Dette betyr at det er raskere å forbedre/redigere et gråtonebilde fordi det er mindre data å holde styr på. Bruk rgb2gray for å konvertere bildet til gråtoner. (Imrotateringsfunksjonen ble brukt fordi bildene våre kom horisontalt - denne kodelinjen kan være nødvendig i din versjon.)

• %konverter til gråtoner og roter
• I = imread (ControlFile);
• I = rgb2gray (I);
• I = imrotate (I, 90);

Deretter viser du bildet. Delplotfunksjonen brukes slik at testbildet vil kunne være ved siden av kontrollen i senere trinn.

• %vise
• Figur 1);
• delplot (1, 2, 1)
• imshow (I);
• tittel (ControlFile);

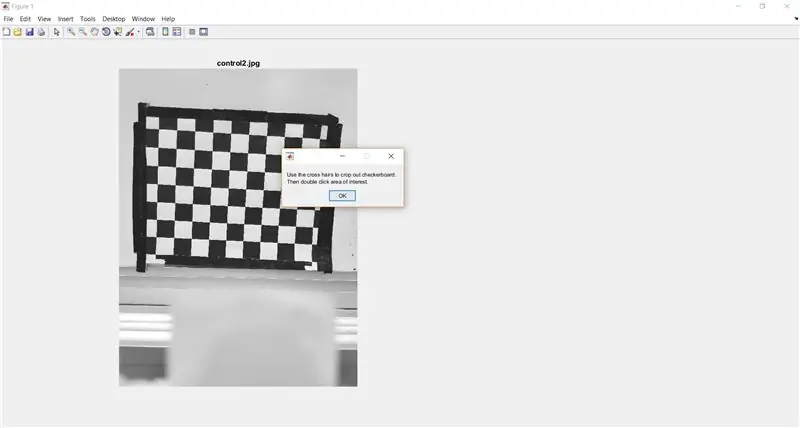
Bruk imcrop for å be brukeren om å beskjære sjakkbrettet ut av hele bildet. Følgende kode viser også en meldingsboks for å gi instruksjoner til brukeren.

• %beskjære ut sjakkbrett for analyse
• waitfor (msgbox ({'Bruk krysshårene til å beskjære brett.', 'Dobbeltklikk deretter på interesseområde.'}));
• I_crop = imcrop (I);

Bruk imbinarize til å binære bildet.

I_binary = imbinarize (I_crop);

Trinn 4: Beregn bredden på de hvite firkantene på sjakkbrettet

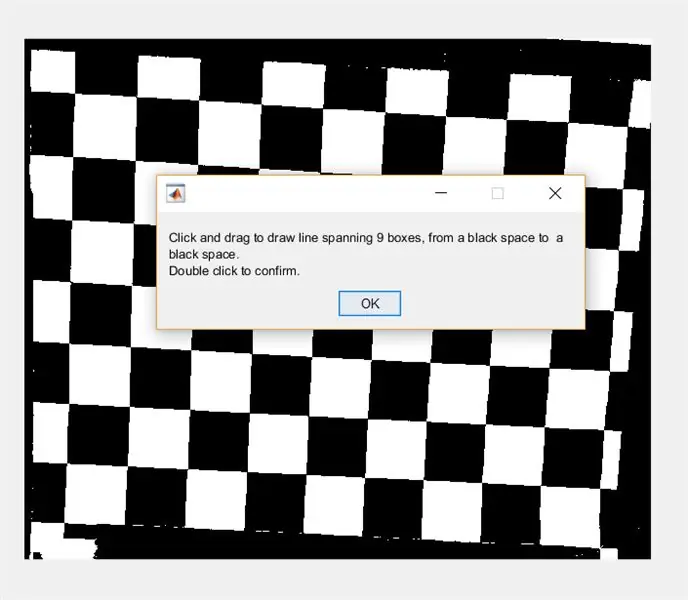
Deretter ber du brukeren om å tegne en linje over bildet ved hjelp av imline. Denne linjen skal gå horisontalt over sjakkbrettet. Den skal starte og ende på en svart firkant (det spiller ingen rolle hvor)- dette er fordi vi skal måle bredden på de hvite rutene, ikke de svarte.

• %trekker linje
• Figur 1)
• delplot (1, 2, 1)
• imshow (I_binary);
• waitfor (msgbox ({'Klikk og dra for å tegne linje som strekker seg over 9 bokser, fra et svart mellomrom til et svart mellomrom.', 'Dobbeltklikk for å bekrefte.'}));
• linje = imline;
• posisjon = vent (linje);
• endepunkter = line.getPosition;

Pakk ut X- og Y -koordinatene for endepunktene for den tegnet linjen.

• X = endepunkter (:, 1)
• Y = endepunkter (:, 2);

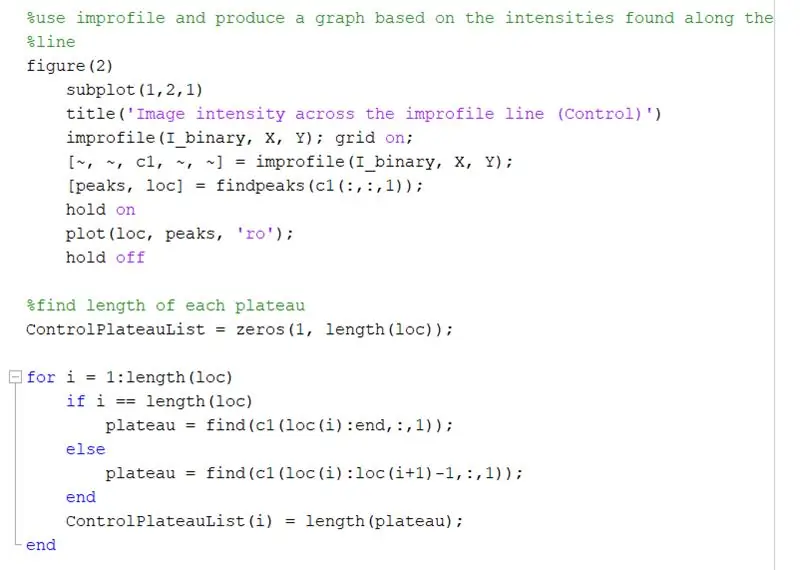
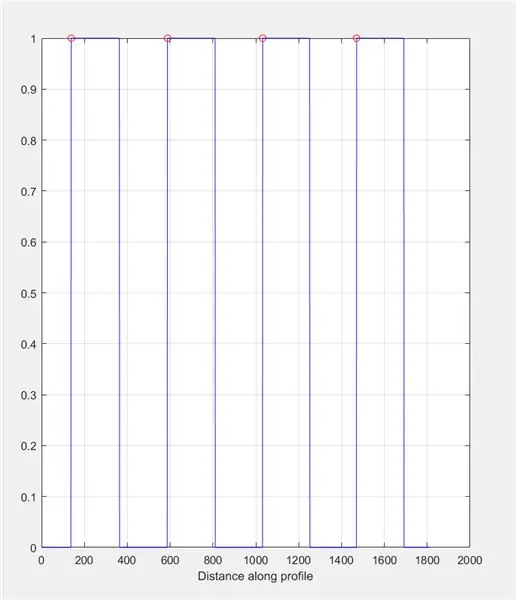
Bruk improfiler til å lage en graf basert på intensitetene som er funnet langs den tegnede linjen. Dette skal ligne en firkantbølge som spenner fra 0 (svart) til 1 (hvit). Beregn toppene og deres plasseringer også.

• figur (2)
• delplot (1, 2, 1)
• tittel ('Bildeintensitet på tvers av den uprofile linjen (kontroll)')
• improfile (I_binary, X, Y); rutenett på;
• [~, ~, c1, ~, ~] = improfile (I_binary, X, Y);
• [topper, loc] = findpeaks (c1 (:,:, 1));
• vent litt
• plot (loc, topper, 'ro');
• hold av

Finn lengden på hvert platå på den improfile grafen ved å bruke en for -løkke. Kjør for -løkken for samme mengde topper som det er i den improfile grafen. For å beregne lengden på hvert platå, bruk "finn" -funksjonen for å finne alle stedene der det er en "1" i stedet for en "0" intensitetsverdi. Beregn deretter lengden på matrisen for å få den totale lengden på platået, som skal være lik bredden på en hvit firkant i piksler. ControlPlateauList = nuller (1, lengde (loc));

for i = 1: lengde (loc)

hvis jeg == lengde (loc)

platå = finn (c1 (loc (i): ende,:, 1));

ellers

platå = finn (c1 (loc (i): loc (i+1) -1,:, 1));

slutt

ControlPlateauList (i) = lengde (platå);

slutt

Trinn 5: Gjenta trinn 3 og 4 for testbildet

*Merk: Når du tegner den uprofile linjen på testbildet, må du tegne den på tvers av rutene som tilsvarer linjen du tegnet på kontrollbildet.

Trinn 6: Beregn forstørrelsen på objektivet

De forstørrede målingene beregnes ved å dele gjennomsnittet av lengden på platået, som ble beregnet i trinn 5, med gjennomsnittet av lengden på kontrollplatået, som ble beregnet i trinn 4. Dette er beregnet til å være 1,0884.

forstørrelse = gjennomsnitt (plateauList)/gjennomsnitt (ControlPlateauList);

Trinn 7: Finne R-kvadrat og brukerens resept via interpolasjon

Bruke koden:

• md1 = fitlm (GivenPrescription, MagArray);
• Rsquared = md1. Rsquared. Ordinary;

Vi kan finne R-kvadratverdien til grafen GivenPresciption (våre linsers gitte verdier) mot MagArray (en rekke forstørrelsesmålingene vi beregnet tidligere). Ved å ha en høy nok R-kvadratverdi, kan det antas at det er en sterk nok korrelasjon til å rettferdiggjøre bruken av denne metoden. For dette spesielle tilfellet var R-kvadratverdien 0,9912, noe som antyder en sterk korrelasjon og derfor er begrunnet i å bruke denne metoden i analyse.

Bruke funksjonen:

Resept = interp1 (MagArray, GivenPrescription, forstørrelse, 'lineær');

Vi kan interpolere den tilsvarende reseptverdien (på x-aksen) i vårt forstørrelsesforhold (en verdi på y-aksen) og finne hva brukerens resept er.

Interpolering av data er viktig for at denne metoden skal fungere, da den lar oss gjøre forutsetninger om informasjon vi ikke har, basert på informasjonen vi har. Selv om en linje med best passform teknisk sett ville vært en sterkere kandidat for denne antagelsen, vil det å skape grenser for å redusere antall utganger tjene den samme effekten som reseptbelagte briller uansett har trinnvise ensartede verdier. Dette forklares i senere trinn.

Trinn 8: Viser brukerens resept på en graf

Bruk følgende kode:

• figur;
• plot (GivenPrescription, MagArray, '-g')
• vent litt
• plot (resept, forstørrelse, 'bp')
• hold av
• Nett
• legend ('Data', 'Interpolated Points', 'Location', 'NW')

Vi kan plotte en graf som viser forstørrelsesforholdene versus den gitte resepten med en grønn linje og de funnet dataene for vår beregnede forstørrelse kontra vår interpolerte resept med en blå stjerne. Deretter merker legenden tittelen, x-aksen og y-aksen og plasserer forklaringen øverst i venstre hjørne.

Trinn 9: Begrens reseptet

Følgende kode brukes for å produsere avrundingen for reseptet:

• hvis resept <= 1.125

  CalculatedPrescription = '1.0';

• elseif Resept <= 1.375

  CalculatedPrescription = '1,25';

• elseif Resept <= 1.625

  CalculatedPrescription = '1.5';

• elseif Resept <= 1.875

  CalculatedPrescription = '1.75';

• elseif Resept <= 2,25

  CalculatedPrescription = '2.0';

• elseif Resept <= 2.625

  CalculatedPrescription = '2.5';

• elseif Resept <= 3

  CalculatedPrescription = '2,75';

• elseif Resept <= 3.375

  CalculatedPrescription = '3.25';

• ellers

  CalculatedPrescription = 'ukjent';

• slutt

Reseptet som finnes gjennom interpolasjon, gjenspeiler ikke nødvendigvis den faktiske resepten - dette er fordi det alltid vil være små variasjoner i analysen av bildet på grunn av menneskelige feil. Derfor trenger vi dette trinnet for å klassifisere den faktiske resepten.

Reseptene som er gitt starter vanligvis fra 1,0 dioptrier og øker med.25 i reseptene, så etter å ha beregnet reseptet vil vi bestemme reseptet som passer best til det brukeren kan trenge. Etter beregning av resept kjører vi den gjennom de gitt If -setningene for å kontrollere verdien og bestemme hvilken resept som er nødvendig. Noe mindre enn eller lik 1.125, så er reseptet 1.0. Noe mindre enn eller lik 1.375, reseptet er 1.25. Noe mindre enn eller lik 1.625, reseptet er 1.5. Noe mindre enn eller lik 1.845, reseptet er 1.75. Og så videre.

Vi har verdiene økende siden vi sjekker om verdiene er mindre enn. Hvis vi gjorde at verdiene minket, så ville den første if -setningen lese den første if -setningen hele tiden. Hvis resept er den minste, vil vi at den skal gjenkjenne den som den minste med en gang, så derfor er den minste verdien det vi begynte med. Alt høyere enn den høyeste verdien betyr at reseptet ikke er innenfor rekkevidde med dataene våre, så det vil gi "Ukjent" strengavlesning.