Bioimpedansanalyse (BIA) Med AD5933: 9 trinn

2024 Forfatter: John Day | [email protected]. Sist endret: 2024-01-30 11:23

Jeg har vært interessert i å lage en bioimpedansanalysator for målinger av kroppssammensetning, og mine tilfeldige søk fortsatte å finne et design fra klassen Biomedical Instrumentation 2015 ved Vanderbilt University. Jeg har jobbet gjennom designet og forbedret det litt. Jeg vil gjerne dele funnene mine med deg. Ta det du kan bruke fra denne "gjennomgangen" hvis noe ikke er klart, vennligst foreslå forbedringer. Jeg kan en dag skrive tankene mine i en mer sammenhengende form, men foreløpig håper jeg at du kan bruke det du ser her. (Hvis du tror du kan skrive dette opp og forbedre det, er du velkommen)

Teddy

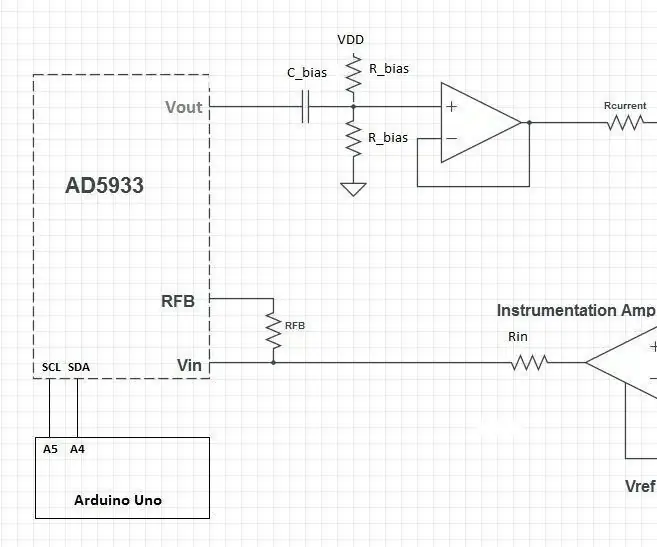
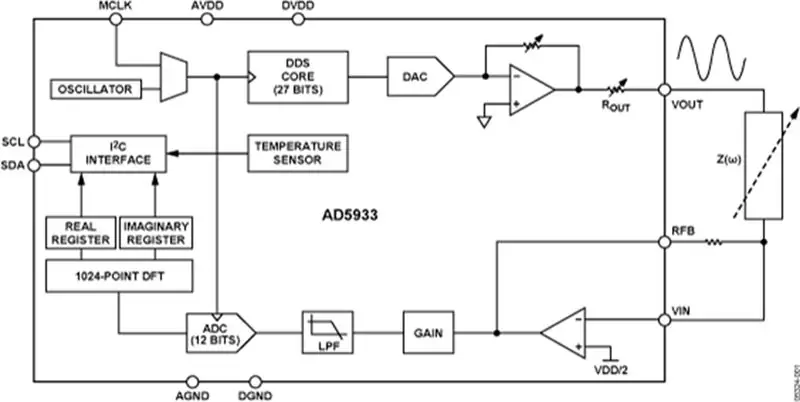
Denne designen består av AD5933-brikken og en tilpasset analog front-end (AFE) som grensesnitt mellom AD5933 og karosseriet. AD5933 måler deretter, og resultatene kan deretter behandles av en mikrokontroller (f.eks. En Arduino).

Hvis du planlegger å bruke Arduino som en strømforsyning, må du sørge for at drifts- og instrumenteringsforsterkere (op-ampere og in-ampere) støtter såkalte "single supply" -spenninger og har jernbane-til-rail-spesifikasjoner.

(I det følgende skal jeg bruke en strømforsyning (fra en Arduino) på 5V og innstillingen for område 1 på AD5933.)

Trinn 1: Re-bias-stadiet

Den første delen av AFE er en re-bias-fase. Utgangsspenningssignalet er ikke sentrert i midten av forsyningsspenningsområdet (VDD/2). Dette korrigeres ved å bruke en kondensator for å blokkere DC -delen av signalet og sende den gjennom en spenningsdeler for å legge en DC -forskyvning tilbake i signalet.

De to re-bias-motstandene kan ha en hvilken som helst verdi så lenge de er like. Den spesifikke verdien av hetten er heller ikke viktig.

Re-bias-trinnet fungerer som et høypassfilter og har derfor en cutoff-frekvens:

f_c = 1 / (2 * pi * (0,5 * R) * C)

Sørg for at cutoff -frekvensen er noen tiår under minimumsfrekvensen du planlegger å bruke. Hvis du planlegger å bruke 1 kHz i applikasjonen din, bør du gå for caps og motstandsverdier som vil gi deg en cutoff-frekvens i størrelsesorden 1-10 Hz.

Den siste delen av dette stadiet er en op-amp som er satt opp for å være en spenningsfølger. Dette er for å sikre at motstandsverdiene ikke forstyrrer neste trinn

Trinn 2: Strømfølermotstand

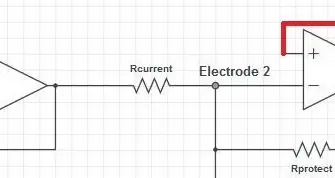
Den første delen av neste trinn er den nåværende sensormotstanden. Strømmen gjennom denne motstanden vil være den samme strømmen som forsterkeren vil prøve å opprettholde gjennom kroppen. Sørg for at strømmen er i samsvar med sikkerhetsstandardene IEC6060-1*:

Under frekvenser på 1 kHz er maksimalt 10 microAmps (RMS) tillatt gjennom kroppen. Ved frekvenser over 1 kHz gir følgende ligning maksimal tillatt strøm:

Maks AC strøm <(minimum frekvens i kHz) * 10 microAmps (RMS)

Forholdet mellom toppamplituden til et AC -signal og dens RMS -verdi er: Peak = sqrt (2) * RMS. (10 microAmps RMS tilsvarer 14 microAmps toppamplitude)

Ved å bruke Ohms Law på motstanden kan vi beregne motstandsverdien som vil overholde sikkerhetsstandarden. Vi bruker eksitasjonsspenningen fra AD5933 og maksimal strømverdi:

U = R * I => R = U / I

F.eks. ved bruk av Range 1 -innstillingen Upeak = 3V / 2 = 1,5V (eller 1V @3,3V)

Ved å bruke 14 microAmp toppverdien ovenfra får jeg en motstandsverdi på minst 107kOhms

Referanser:

* Analoge enheter: "Bio-impedans-kretsdesign for kroppsslitte systemer"

Trinn 3: Trans-konduktansforsterkeren

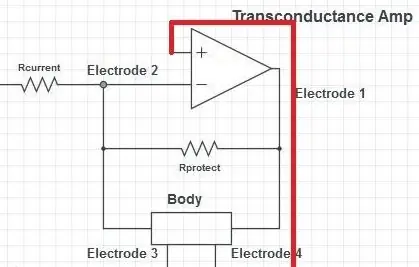
Etter den nåværende sensermotstanderen er det en op-amp i en negativ feedback-konfigurasjon. Dette er et såkalt Load-in-the-Loop-oppsett. Den positive inngangsterminalen til op-amp er koblet til en VDD/2-spenning. Op-amp vil nå prøve å justere utgangen i motsatt retning til eksitasjonssignalet slik at spenningen ved den negative terminalen vil være lik VDD/2. Dette vil gi et seesawing potensial som skyver og trekker strømmen gjennom kroppen.

Strømmen hentet fra den negative terminalen til op-amp er praktisk talt null. All strøm gjennom strømfølende motstand må derfor flyte gjennom kroppen. Dette er mekanismen som gjør dette oppsettet til en trans-konduktansforsterker (også kalt en spenningskontrollert strømkilde, VCCS).

Op-amp kan bare opprettholde strømmen hvis kroppens impedans ikke er for høy. Ellers ville op-amp-utgangen bare maks ut ved forsyningsspenningen (0 eller 5 V). Maksimal spenning som kan opprettholdes er VDD/2 + Upeak (2,5 + 1,5V = 4V @ 5V forsyning). Spenningsmarginene til op-amp skal trekkes fra denne verdien, men hvis op-amp har rail-to-rail spesifikasjoner ville det bare være en liten mengde. Maksimal impedans som op-amp kan drive er derfor:

Z <(VDD / 2 + Upeak) / Imax

(I mitt oppsett Z <4V / 14 microAmps = 285 kOhms, wish is plenty to cover the impedance range of the body)

Beskyttelsesmotstanden har en veldig stor verdi (1-1,5 MOhms) sammenlignet med kroppen (ca. 100kOhms), og for alle normale operasjoner vil dette ikke trekke noen merkbar strøm, og impedansen til parallellforbindelsen domineres av kroppens impedans. Hvis kroppens impedans skulle stige (f.eks. Pads som løsner) kan strømmen gå gjennom motstanden og maksimal utgang av op-amp vil ikke skape ubehagelige spenninger i putene.

Trinn 4: Instrumenteringsforsterkeren

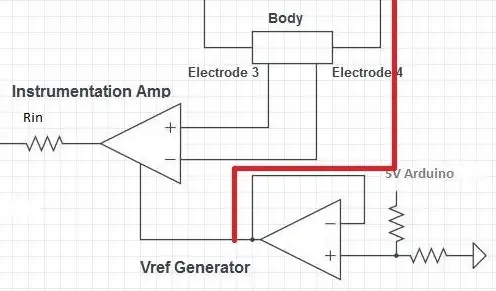
Det neste trinnet er instrumenteringsforsterkeren (in-amp) som måler spenningen over kroppen. Spenningen over kroppen svinger rundt 0V, men AD5933 trenger inngangsspenningen for å være i et positivt område. Forsterkeren legger derfor til en DC-forskyvning av VDD/2 til det målte spenningssignalet.

VDD/2 -referansen genereres av en spenningsdeler. Enhver verdimotstand kan brukes så lenge de er like. Spenningsdeleren skilles fra impedansen til resten av kretsen av en spenningsfølger. Utgangen til spenningsfølgeren kan deretter videresendes til både forsterkeren og trans-konduktansforsterkeren.

Trinn 5: Inngangsfasen og kalibrering

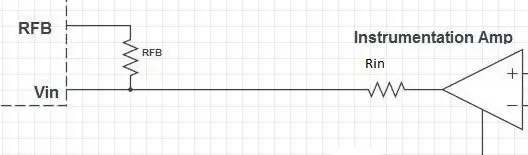
Inngangstrinnet til AD5933 inneholder en op-amp i negativ feedback-konfigurasjon. Det er to motstander: en i serie (Rin) og en parallelt (RFB). Gevinsten til op-amp er gitt av

A = - RFB / Rin

Gevinsten til inngang op-amp og in-amp (og PGA) må sørge for at signalet som går inn i ADC til AD5933 alltid er innenfor 0V og VDD.

(Jeg bruker en enhetsforsterkning i forsterker og motstandsverdier som vil gi ca A = 0,5)

Inne i AD5933 vil ADC konvertere spenningssignalet til a til et digitalt signal. Spenningsområdet fra 0V til VDD konverteres til det digitale området 0-128 (2^7). (Dokumentasjonen er ikke klar om dette, men en grundig undersøkelse av tomtene i [1] og noen eksperimenter fra min side bekrefter dette.)

Inne i DFT -modulen er det en annen skalering på 256 (1024/4, se [1]) før resultatet blir lagret i det virkelige og imaginære registeret.

Ved å følge spenningssignalet gjennom AFE, inn i ADC og bruke skalafaktorene nevnt før, er det mulig å anslå forsterkningsfaktoren til å være:

g = (VDD * Rstrøm * Rin) / (256 * PGA * Oppover * RFB * 2^7)

noen kalibrering kan fortsatt være nødvendig, så ta hensyn til noen effekter som ikke er en del av denne matematiske modellen, så må du måle den virkelige forsterkningsverdien ved å måle komponenter med kjent impedans, som motstander. (g = Z / mag, se nedenfor)

Impedansen kan nå beregnes av

Z = g * mag

mag = sqrt (ekte^2 + imaginær^2)

PA = arctan2 (ekte, imaginær) - deltaPA

PA må sannsynligvis kalibreres så vel som det er et systematisk faseskift som en funksjon av frekvens i AD5933. deltaPA vil trolig være en lineær funksjon av frekvens.

Motstanden og reaktansen kan nå beregnes med

R = Z * cos (PA)

X = Z * sin (PA)

Referanser: [1] Leonid Matsiev, "Forbedring av ytelse og allsidighet av systemer basert på enkeltfrekvente DFT-detektorer som AD5933", Electronics 2015, 4, 1-34; doi: 10.3390/electronics4010001

Trinn 6: Advanced Stuff: Spectral Leakage (DC)

Signalet som vi legger inn i AD5933 er en spenning/strøm som en funksjon av tid, men vår viktigste interesse er impedansen som en funksjon av frekvens. For å konvertere mellom tidsdomene og frekvensdomene må vi ta Fourier-transformasjonen av tidsdomenesignalet. AD5933 har en innebygd diskret Fourier transform (DFT) modul. Ved lave frekvenser (under ca. 10 kHz) påvirkes bygget i DFT av aliasing og spektrallekkasjer. I [1] går han gjennom matematikken om hvordan man kan korrigere spektrallekkasjen. Essensen i dette er å beregne fem (pluss to) konstanter for hvert frekvenstrinn i feien. Dette kan enkelt gjøres f.eks. av Arduino i programvare.

Lekkasjen kommer i to former: en DC -lekkasje som er additiv i naturen og en AC -lekkasje som er multiplikativ i naturen.

DC -lekkasjen stammer fra det faktum at spenningssignalet ved ADC ikke svinger rundt 0V, men rundt VDD/2. Et likestrømnivå på VDD/2 skal tilsvare en digital likestrømavlesning på ca. 64 (angitt delta i [1]).

Trinnene for å korrigere DC -spektrallekkasjen:

1) Beregn konvoluttfaktoren E for gjeldende frekvens.

2) Beregn de to forsterkningsfaktorene GI (reell) og GQ (imaginær)

3) Trekk delta * GI fra verdien av det virkelige registeret og delta * GQ fra verdien av det imaginære registeret

Referanser:

[1] Leonid Matsiev, "Forbedring av ytelse og allsidighet i systemer basert på

Enfrekvente DFT-detektorer som AD5933 , Electronics 2015, 4, 1-34; doi: 10.3390/electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Based on AD5933 Integrated Circuit", Metrol. Mål. Syst., Bind. XXII (2015), nr. 1, s. 13–24.

Trinn 7: Avanserte ting: Spektral lekkasje (AC)

Som likelekkasjen kan AC -lekkasjen korrigeres matematisk. I [1] kalles motstanden og reaktansen henholdsvis A*cos (phi) og A*sin (phi), hvor A tilsvarer størrelsen på impedansen og phi tilsvarer fasevinkelen (PA).

Trinnene for å korrigere AC -spektrallekkasjen:

1) Beregn konvoluttfaktoren E (ikke den samme som for DC) for gjeldende frekvens.

2) Beregn de tre faktorene a, b og d. (ca. verdier ved høyere frekvenser: a = d = 256 og b = 0)

3) Motstand (Acos (phi)) og reaktans (Asin (phi)) kan nå beregnes i digitale enheter

Referanser: [1] Leonid Matsiev, "Forbedring av ytelse og allsidighet av systemer basert på enkeltfrekvente DFT-detektorer som AD5933", Electronics 2015, 4, 1-34; doi: 10.3390/electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Based on AD5933 Integrated Circuit", Metrol. Mål. Syst., Bind. XXII (2015), nr. 1, s. 13–24.

Trinn 8: Avanserte ting: den teoretiske gevinstfaktoren

Gitt den matematiske modelleringen av DFT, bør det også være mulig å modellere hele AFE matematisk. Matematisk kan spenningssignalet beskrives med en sinusfunksjon med en gitt fast frekvens, en DC -forskyvning og en AC -svingning med en maksimal amplitude. Frekvensen endres ikke under et frekvenstrinn. Siden forsterkningsfaktoren bare endrer størrelsen på impedansen og ikke PA, vil vi her ikke være bekymret for noe faseskift indusert på signalet.

Her er en kort oppsummering av spenningssignalet når det forplanter seg gjennom AFE:

1) Etter re-bias-trinnet er AC-amplituden fremdeles Upeak = 1,5V (1V @ VDD = 3,3V) og DC-forskyvningen er endret til VDD/2.

2) I den nåværende sensormotstanden er spenningen stille den samme som forrige trinn …

3) … men på grunn av vippespenningen til op-amp har AC-svingningene en størrelse på Z*Upeak/Rcurrent. (DC -forskyvningen avbrytes av op -ampere -referansespenningen til VDD/2 - vippepunktet på vippen - og blir en kraftig jord i denne delen av kretsen)

4) Enhetsforsterkeren legger DC-forskyvningen til VDD/2 tilbake og videresender signalet til inngangstrinnet til AD5933

5) Op-amp i inngangstrinnet har en forsterkning på A = -RFB/Rin og AC-amplituden blir derfor (Z*Upeak/Rcurrent)*(RFB/Rin)

6) Like før ADC er det en programmerbar forsterkningsforsterker (PGA) med to innstillinger en forsterkning på 1 eller 5. Spenningssignalet ved ADC blir derfor: PGA*(Z*Upeak/Rcurrent)*(RFB/Rin)

ADC konverterer v (t) -signalet til et digitalt signal x (t) = u (t) / VDD * 2^7 med en 12 -bits nøyaktighet.

Størrelsen A er koblet til impedansen Z med forsterkningsfaktoren, k, som A = k * Z og har en omtrentlig verdi på k = PGA * Upeak * RFB * 2^7 / (VDD * Rstrøm * Rin).

Hvis du liker å jobbe med gain-faktor i stedet g = 1 / k og Z = g * A.

Trinn 9: Avanserte ting: PA -skiftet

I [2] finner de et systematisk skifte i PA som en funksjon av frekvens. Dette skyldes en tidsforsinkelse mellom DAC der eksitasjonssignalet genereres og DFT der det innkommende signalet må vikles med det utgående signalet.

Skiftet er preget av antall klokke-sykluser signalet er forsinkelse mellom DAC og DFT internt i AD5933.

Referanser: [1] Leonid Matsiev, "Forbedring av ytelse og allsidighet av systemer basert på enkeltfrekvente DFT-detektorer som AD5933", Electronics 2015, 4, 1-34; doi: 10.3390/electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Based on AD5933 Integrated Circuit", Metrol. Mål. Syst., Bind. XXII (2015), nr. 1, s. 13–24.